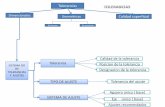
2 ecuaciones dimensionales

2 | Ecuaciones Dimensionales Fsica | Derum

6 Pre facultativos de Ingeniera

2 | Ecuaciones Dimensionales

Son ecuaciones que nos permiten comprobar si una formula es

correcta o no, tambin para dar unidades o dimensiones a las

incgnitas de un problema.

Las ecuaciones dimensionales se obtienen de la siguiente manera,

teniendo una ecuacin cualquiera:

Se denomina ecuacin dimensional a la siguiente expresin:

| | | | | | Ecuacin Dimensional

Donde el smbolo | | se lee dimensin.

Ejemplo:

| | : Se lee dimensin de V | | : Se lee dimensin de V0 | | : Se lee dimensin de a | | : Se lee dimensin de t

Para hallar la ecuacin dimensional de una determinada formula fsica

o qumica, simplemente se aplica el smbolo | | a cada termino de la

ecuacin o formula.

Ejemplo:

Ecuacin Ecuacin Dimensional

| | | | |

| | |

| | | |

| || |

Tomar en cuenta lo siguiente

Sean A y B dos magnitudes fsicas, en los trminos de una ecuacin

dimensional, se cumple lo siguiente.

1.-Multiplicacion | | | || |

Ejemplo: Sean = aceleracin = velocidad

| | | || |

2.-Division

|

|

| |

| |

Ejemplo: Sean = distancia = tiempo

|

|

| |

| |

Para evaluar las dimensiones en donde existe multiplicacin y divisin

de magnitudes, la dimensin se reparte para cada una de las

magnitudes.

3.- Radicacin

| |

Dimensiones en el Sistema Absoluto

MAGNITUD FISICA

SIMBOLOS DE LAS UNIDADES

DIMENSION

Longitud m, cm, ft L

Masa Kg, g, lb M

Tiempo s T

Temperatura K

Cantidad de sustancia

mol N

Intensidad de corriente

A I

Fsica | Derum 2 | Ecuaciones Dimensionales

Pre facultativos de Ingeniera 7

En donde L, M, T son las dimensiones que ms se utilizan y estas estn

representadas con las inciales de su magnitud fsica.

Sabiendo que de las magnitudes fundamentales se obtienen

magnitudes derivadas, en la siguiente tabla se muestran las

dimensiones de algunas magnitudes derivadas ms usadas en el

sistema absoluto.

Dimensiones en el Sistema Tcnico

En la siguiente tabla se muestran las dimensiones de las magnitudes

mas empleadas en el sistema tcnico.

Principio de Homogeneidad

Principio que nos indica que solo se pueden sumar o restar

magnitudes que tengan la misma unidad de medida (mismas

dimensiones).

Ejemplo:

Adems se dice que una ecuacin es dimensionalmente correcta o

cumple con el principio de homogeneidad, cuando cada uno de sus

trminos tiene las mismas dimensiones.

Ejemplo: Analizar la siguiente ecuacin para comprobar si la formula

es dimensionalmente correcta:

Donde:

= velocidad(m/s), = aceleracin(m/s2), = tiempo(s)

Si la formula es dimensionalmente correcta debe cumplir con el

principio de homogeneidad, por lo tanto cada uno de sus trminos

deben tener las mismas dimensiones.

Hallando la ecuacin dimensional tenemos:

| | | | | |

Analizando cada uno de los trminos:

Primer trmino

| |

Segundo termino

| |

Tercer termino

| | | || |

MAGNITUD FISICA

SIMBOLO DE LA UNIDAD

DIMENSION

rea m2 L2

Volumen m3 L3

Velocidad m/s LT 1

Aceleracin m/s2 LT 2

Fuerza N = Kgm/s2 MLT 2

Presin Pa = N/m2 ML 1T 2

Densidad g/cm3 ML 3

Energa J = Nm ML2T 2

Potencia Watt = Nm/s ML2T 3

MAGNITUD FISICA

SIMBOLOS DE LAS UNIDADES

DIMENSION

Longitud m, cm, ft L

Fuerza Kgf, lbf F

Tiempo s T



Al ver que cada trmino tiene las mismas dimensiones concluimos que

la ecuacin es dimensionalmente correcta.

De lo visto anteriormente podemos concluir que el principio de

homogeneidad nos sugiere expresar la ecuacin de la siguiente

manera:

| | | | | |

Principio de Homogeneidad

Nota: observa que debido al principio de homogeneidad los signos de

suma y resta en las ecuaciones dimensionales se convierten en

igualdad. EJEMPLO:

| | | | | | | | | | | |

Dimensin de una constante

Las dimensiones de cualquier constante ya sean, funciones

trigonomtricas, logaritmos y todo aquello que representa a un

nmero, se remplaza por 1, siempre y cuando no se encuentren como

exponentes.

| | | |

| | | |

La resolucin de ejercicios de ecuaciones dimensionales se los puede

realizar de dos formas:

1.- Trabajando con sus dimensiones (L,M,T)

2.- Trabajando con sus unidades (m,Kg,s).

Propiedad de exponentes que se utilizaran en la

resolucin de Ecuaciones Dimensionales

1.-

2.-

3.-

4.-



Problemas Resueltos Ecuaciones Dimensionales

PROBLEMA 1: En la ecuacin , determinar las

dimensiones de k. En donde: g= gravedad, m=masa, x=distancia,

d= densidad y v= volumen.

Solucin: Nos piden las dimensiones de k, para los cual lo primero que

debemos hacer es reconocer las unidades y dimensiones de cada

magnitud por lo tanto tenemos:

| |

| |

| |

| |

| |

Primera forma, consiste en trabajar con sus dimensiones. Por lo tanto

hallando la ecuacin dimensional de tenemos:

| || | | || | | || || |

Debido al principio de homogeneidad el signo de suma se convierte en

igualdad, por lo tanto la ecuacin queda:

| || | | || | | || || |

De esta ltima ecuacin tomamos solo los dos primeros trminos:

| || | | || |

Despejando | | de esta ecuacin tenemos:

| | | || |

| |

Remplazando las dimensiones en esta ecuacin se tiene:

| |

Aplicando ley de exponentes y simplificando tenemos:

| |

Segunda forma, consiste en trabajar con unidades por lo tanto

remplazando unidades en la ecuacin tenemos:

Utilizando ley de exponentes y despejando k tenemos:

Aplicando dimensiones

| | | | | |

Recordando que las dimensiones de | | | |

| |



Claramente podemos ver que este resultado es el mismo obtenido

anteriormente, por lo tanto podemos escoger cualquiera de las dos

formas.

PROBLEMA 2: Determinar las dimensiones de | | si la

expresin dada es dimensionalmente correcta.

Donde:

w= velocidad angular (rad/s)

t = tiempo (s)

d= distancia (m)

Solucin: Nos piden hallar la dimensin de la multiplicacin de las

dimensiones de x y y z, pero antes debemos hallar las dimensiones que

tienen cada una de estas.

Obteniendo las dimensiones de las magnitudes tenemos:

| |

| |

| |

Hallando la ecuacin dimensional, se tiene:

| | | |

| |

| |

| || |

| | | |

| |

Debido al principio de homogeneidad los signos de suma y resta se

convierten en igualdad, por lo tanto la ecuacin queda:

| | | |

| |

| |

| || |

| | | |

| |

Para hallar la dimensin de | | de la ecuacin tomamos solo los

dos primeros trminos:

| | | |

| |

| |

| || |


| | | || | | | | |

| |

Remplazando dimensiones en esta ecuacin y recordando que la

dimensin de una constante es 1, nuestra ecuacin queda:

| |


| |

Para hallar la dimensin de | | de la ecuacin tomamos la igualdad

que existe en el tercer trmino:

| | | |


| | | |


| |

Para hallar la dimensin de | | de la ecuacin tomamos el primer y

el tercer trmino:

| | | |

| |

| | | |

| |



La ltima ecuacin es equivalente a esta otra:

| | | |

| |

| |

| |


| | | || |

| || |

Remplazando dimensiones en esta ecuacin y recordando que la

dimensin de una constante es 1, nuestra ecuacin queda:

| |


| |

Una vez teniendo las dimensiones de x y y z de acuerdo con el

problema realizamos la multiplicacin de sus dimensiones.

| | | || || |

| |

| |

| |

PROBLEMA 3: La potencia (P) que requiere la elice mayor de un

helicptero viene dada por la siguiente formula.

En donde: k= numero; R=radio de hlice; w=velocidad angular;

D=densidad del aire. Hallar la expresin final de la formula.

Solucin: Nos piden hallar la expresin final de la formula, para lo cual

debemos hallar los valores de x, y y z.

Obteniendo las dimensiones de las magnitudes, tenemos:

| |

| |

| |

| |

| |

Hallando la ecuacin dimensional.

| | | | | | | | | |

Remplazando dimensiones

Aplicando propiedad de exponentes.

Por propiedad de exponentes, si am=an entonces m=n

Por lo tanto igualamos exponentes para cada base, de la ecuacin

Finalmente remplazando los valores de x, y y z en la ecuacin inicial,

para poder obtener la expresin final tenemos:



IMPORTANTE: Cuando se tengan: sen, cos, logaritmos o algo que

representa a un nmero y este en el exponente de alguna unidad o

dimensin no es correcto aplicar la definicin de dimensiones para

una constante y remplazarla por uno. Estas se operan normalmente.

Lo que le indicamos es que nunca se deben aplicar dimensiones a los

exponentes. Ejemplos:

| |

| |

PROBLEMA 4: Para estudiar el comportamiento de un gas real,

aire por ejemplo, se dispone de ecuaciones de diversas formas, una de

ellas es la de Van Der Waals definido como:

(

)

Donde:

P= presin (N/m2)

V= Volumen (m3)

n= N de moles (mol)

T = temperatura (k)

a = constante (m5 Kg/mol2 s2)

b = Constante (m3/mol)

Obtngase las unidades de la constante universal de los gases R.

Solucin: Nos piden hallar las unidades de R.

Obteniendo las dimensiones de las magnitudes tenemos:

| |

| |

| |

| |

| |

| |

Antes de analizar dimensionalmente la ecuacin, desarrollaremos el

producto que existe en el primer miembro, con el propsito de facilitar

la resolucin del problema:

(

)

Hallando la ecuacin dimensional, se tiene:

| || | | || || | |

| | | |

| | || | | || || |

Debido al principio de homogeneidad los signos de suma y resta se

convierten en igualdad, por lo tanto la ecuacin queda:

| || | | || || | |

| | | |

| | || | | || || |

De esta ltima ecuacin tomamos el primer y el tercer trmino:

| || | | || || |


| | | || |

| || |


| |


| |



Como el problema nos piden en unidades y no en sus dimensiones,

recordando que | | | | | | | | | |,

la ecuacin expresada en sus unidades queda:

| | | || | | |

| || |

2 ecuaciones dimensionales

Documents

Transcript of 2 ecuaciones dimensionales