APUNTE DE CÁLCULO

CALCULO DIFERENCIAL JUAN ESPINOZA B

TEOREMA DE LA FUNCION INVERSA

Sea f una función continua y creciente, cuyo dominio es el intervalo I

y cuyo rango es J, entonces f tiene una inversa g, que es una función

continua y creciente con dominio J y rango I, más aún tenemos que:

xxgf =))(( , para todo x en el intervalo J (1)

xxfg =))(( , para todo x en el intervalo I (2)

Si f es decreciente en I, en vez de creciente, entonces el mismo

resultado es válido con g decreciente en J. Si 0)(,

≠xf en el interior de I

entonces g es derivable en el interior de J.

Podemos interpretar gráficamente, las fórmulas (1) y (2) del teorema,

diciendo que g es el operador (función) que invierte la acción de f. Es el

operador inverso o la aplicación inversa. Cualquier acción de f la anula g.

Si una función tiene derivada, entonces podemos usar el teorema

para decidir si la inversa f es una función. Simplemente calculamos ,f y si

esta cantidad es siempre positiva o siempre negativa en el dominio de f,

entonces la inversa debe ser una función.

EJEMPLO: Dada la función:

21)(

x

xxfy

+== para ∞<< +x1 ∞<< +x1

X

Y

I

J y = g(x)

x = f(y)

0

J

I

X

Y

y = f(x)

0

APUNTE DE CÁLCULO

CALCULO DIFERENCIAL JUAN ESPINOZA B

Determinar su rango y decidir si su inversa es una Función.

SOLUCION: Primero calculamos la derivada de f.

( )22

2

1

1,

x

xy

+

−=

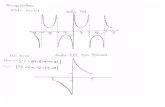
Puesto que la derivada es negativa para ∞<< x1 , la función es

decreciente (Ver figura).

Tenemos que 2

1)1( =f y 0)( =

+∞→xf

xlim 0)( =xf . Por lo tanto el

rango es el intervalo

21 ,0 .

Por el teorema de la Función inversa

sabemos que f tiene una Función

Inversa Continua g con dominio

21 ,0 y rango ] [+∞,1 y es

decreciente. Esta inversa g está

determinada por la ecuación

)(yfx=

21

1

yx

+= ó 02 =+− xyxy

Despejando y en esta ecuación de segundo grado, y escogiendo la

rama apropiada tenemos:

2

10 ;

2

411)(

2

<<−+== xx

xxgy

DERIVADAS DE LAS FUNCIONES TRIGONOMETRICAS INVERSAS

TEOREMA: Sea )sen(xArcy = . Entonces:

o

APUNTE DE CÁLCULO

CALCULO DIFERENCIAL JUAN ESPINOZA B

21

1

xdx

dy

−= si 11 <<− x

DEMOSTRACION: Por la definición de las Funciones Trigonométricas

Inversas, tenemos:

xy =)sen( , 22

ππ ≤≤−

y

Por teorema de la función inversa sabemos que dx

dy existe para

11 <<− x . Por la regla de la cadena, obtenemos:

xySen =)(

1)( =⋅dx

dyyCos

Obtenemos que Cos 0>y , siempre que

∈

−

2,2

ππy , por lo tanto, de la

relación:

122 =+ yCosySen

Tenemos que: )(1)( 2 ySenyCos −+= , 22

ππ <<−

y

O bien 21)( xyCos −= Porque x = Sen( y)

En conclusión 21

1

)(

1

xyCosdx

dy

−==

2π−

2π

1

-1

-1 1

Y Y

X X 0 0

2π−

2π

Y = sen (x) Y = Arcsen (x)

APUNTE DE CÁLCULO

CALCULO DIFERENCIAL JUAN ESPINOZA B

TEOREMA:

a) Si y = Arccos(x), entonces 11,1

12

<<−

−= − xxdx

dy

b) Si y = Arctan(x), entonces 21

1

xdx

dy

+=

c) Si y = Arccot(x), entonces 21

1

xdx

dy

+−=

d) Si y = Arcsec(x), entonces 1

12 −

=xxdx

dy si 1>x

e) Si y = Arccosec(x), entonces 1

12 −

=−

xxdx

dy, 1>x

DEMOSTRACION: (Parte d)

d) Por definición de la función secante inversa, podemos escribir:

sec( y) = x , 2

0π<≤ y o

2

ππ −<≤− y

Como 0)( >ytan en el primer y tercer cuadrantes por lo tanto, de la

relación )(sec1)( 22 yytan =+ , obtenemos:

tan ,11)(sec 22 −=−+= xyy 1>x

Por regla de la cadena y por teorema de la función Inversa vemos que:

tan 1)( 2 −= xy

( ) 2

1

12

1)(sec 22 −

−= xdx

dyy

12

2 −=

x

xx

Despejando,

1)(sec 22 −

=xy

x

dx

dy como sec(y) = x, entonces,

22 )(sec xy =

Por lo tanto 122 −

=xx

x

dx

dy