Cálculo Integral - 2ª Lista 2013 -...
4
1 2ª Lista de Exercícios – 2013 Integrais Definidas e Cálculo de Área 1. Calcule as seguintes integrais definidas: (a) ∫ + − 3 1 2 2 3 dx x 5 x 4 x 2 (b) ( ) 1 2 3 0 t t t dt − ∫ (c) ∫ − − 6 3 dx 4 x 2. Uma partícula move-se com uma velocidade de v(t) m/s ao longo de um eixo s. Ache o deslocamento e a distância percorrida pela partícula, durante o intervalo de tempo dado. a) v(t) sen(t); 0 t 2 π = ≤ ≤ . b) v(t) cos(t); t 2. 2 π = ≤ ≤ π 3. Uma partícula move-se com aceleração 2 m/s ao longo de um eixo s e tem velocidade 0 v m/s , no instante t 0 = . Ache o deslocamento e a distância percorrida pela partícula durante o intervalo de tempo dado. a) 0 a(t) 2; v 3; 1 t 4 = − = ≤ ≤ b) 0 1 a(t) ; v 2; 0 t 3 5t 1 = = ≤ ≤ + 4. Um país tem 100 bilhões de m 3 de reserva de gás natural. Se A(t) denota o total de gás consumido após t anos, então dA/dt é a taxa de consumo. Se a taxa de consumo é prevista em 5 + 0,01t bilhões de m 3 por ano, qual o tempo aproximado, em anos, em que as reservas estarão esgotadas? Através da integral indefinida podemos calcular a área limitada por uma curva y=f(x) e o eixo Ox, onde a ≤ x ≤ b. Esse link é obtido com o uso do Teorema Fundamental do Cálculo. 5. a) Usando integrais, calcule a área limitada pela reta y=x e o eixo Ox, onde 1 ≤ x ≤ 3. b) Confira o resultado obtido calculando a área com seus conhecimentos do Ensino Médio. −1 1 2 3 −1 1 2 3 x y UNIFACS - Cursos de Engenharia Disciplina: Cálculo Integral Ano: 2013
Transcript of Cálculo Integral - 2ª Lista 2013 -...
1
2ª Lista de Exercícios – 2013
Integrais Definidas e Cálculo de Área 1. Calcule as seguintes integrais definidas:
(a) ∫+−3
1 2
23 dx
x5x4x2 (b) ( )1 2 3
0 t t t dt−∫ (c) ∫− −
6
3 dx4x
2. Uma partícula move-se com uma velocidade de v(t)m/s ao longo de um eixo s. Ache o deslocamento e a distância percorrida pela partícula, durante o intervalo de tempo dado.
a) v(t) sen(t); 0 t2π
= ≤ ≤ . b) v(t) cos(t); t 2 .2π
= ≤ ≤ π
3. Uma partícula move-se com aceleração 2m / s ao longo de um eixo s e tem velocidade 0v m / s , no instante t 0= . Ache o deslocamento e a distância percorrida pela partícula durante o intervalo de tempo dado.
a) 0a(t) 2; v 3; 1 t 4= − = ≤ ≤ b) 01a(t) ; v 2; 0 t 35t 1
= = ≤ ≤+
4. Um país tem 100 bilhões de m3 de reserva de gás natural. Se A(t) denota o total de gás consumido após t anos, então dA/dt é a taxa de consumo. Se a taxa de consumo é prevista em 5 + 0,01t bilhões de m3 por ano, qual o tempo aproximado, em anos, em que as reservas estarão esgotadas?
Através da integral indefinida podemos calcular a
área limitada por uma curva y=f(x) e o eixo Ox,
onde a ≤ x ≤ b. Esse link é obtido com o uso do
Teorema Fundamental do Cálculo.
5. a) Usando integrais, calcule a área limitada pela
reta y=x e o eixo Ox, onde 1 ≤ x ≤ 3.
b) Confira o resultado obtido calculando a área
com seus conhecimentos do Ensino Médio.
−7 −6 −5 −4 −3 −2 −1 1 2 3
−6
−5
−4
−3
−2
−1
1
2
3
x
y
UNIFACS - Cursos de Engenharia Disciplina: Cálculo Integral Ano: 2013
2
6. a) Usando integrais, calcule a área limitada
pelas retas y=x+1, y=-x+5, e os eixos
coordenados Ox e Oy.
b) Confira o resultado obtido calculando a área
com seus conhecimentos anteriores. x
y
-4 4
-4
-2
2
7. Calcule a área determinada pelo gráfico da
função y=x2 +1 (parábola) pela reta y=-2x+4, e
os eixos coordenados Ox e Oy.
x
y
y = 1+x^2
y = -2x+4
8. Determine a área limitada pela parábola y = x2 + 1 e pela reta y = –x + 3 .
9. Visualize os gráficos abaixo e determine a área da região do plano limitada por essas curvas. (a) xy = 4 e x + y = 5. (b) y = 2x, y = 2x - x2, x = 0 e x = 2. (c) y = 2x, y = 1 e y = 2/x
(d) y = x3 – 3x, y = 2x2 (e) y = x3 e y=x2 + 2x (f) y = 9/x, y = 9x, y = x
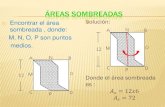
10. Determine o valor das áreas sombreadas nas figuras abaixo. Se possível verifique suas respostas usando áreas conhecidas no Ensino Médio (triângulos, trapézios) ou em um programa computacional. a) b) c) d)
3
Integração de frações racionais por decomposição de frações parciais. 11. Resolva as integrais abaixo.
a) 1x
dx2∫−
b) 6x5x
dx2∫
+− c)
x3x
dx2∫+
d) dx)7x)(1x(
3x2∫ −−
−
e) dxx3x
1xx2
2∫
+
++ f) dx
4x3x
10x52∫
−−
− g) dx
1x
2xx2
2∫
−
++ h) dx
xx2x
6x20x523
2∫
++
++
i) dx x2x
4x2 23∫
−
+ j)
4 2
3 2
3 16
x x dxx x x− +
− −∫ k) 2 2 0dx ax a
≠−∫ l)
( )( )9
5 2x dx
x x−
+ −∫
m) ( )1
20
2 31x dxx+
+∫
n)
( )( )
22
1
4 7 122 3
x x dxx x x
− −
+ −∫
Integrais trigonométricas: 12. Resolva as integrais abaixo.
a) ∫ xdxsen2 b) ∫ xdxsen3 c) ∫ xdxxsencos 25 d) 2 315sen xcos xdx∫
e) sen(3x)cos(5x)dx∫ f) 3 4sen (2x)cos (2x)dx∫ g) 515sen xdx∫ h) ( )5cos 3 3x dx−∫
Obs: Para resolver: e) use a fórmula ))ba(sen)ba(sen)(2/1(bcossena −++= Respostas 1) a) 10/3; b) 1/70; c) 53/2;
2) a) deslocamento=1; distância=1 b) deslocamento=-1; distância=3 3) a) deslocamento= - 6; distância= 13/2 b) deslocamento = 204/25; distância = 204/25 4) aproximadamente 19,62 anos
5) Área igual a 2.
6) Calcule as interseções entre as curvas para depois integrar em cada intervalo conveniente.
4
7) Calcule as interseções entre as curvas para depois integrar em cada intervalo conveniente.
8) 4,5;
9) a) 15 8ln (2)2− ; b) 3 4
ln(2) 3− ; c) 3 2ln(2)
4− + ; d) 71
6; e)
3712
f) 18ln(3);
10) a) 7/3; b) 8/3; c) 5/2; d) 11/4
11) a) C1x
211x
21
−++− lnln b) C3x2x −+−− lnln
c) C3x31x
31
++− lnln d) C7xln6111xln
61
+−+−
e) 1 7ln ln 33 3
x x x C+ − + + f) 2 ln 4 3ln 1x x C− + + +
g) 2ln 1 ln 1x x x C+ − − + + h) C1xx 61x
9++−+
+− lnln
i) Cx22x 2x2
+−−+ lnln j ) x + 2 1 1 11ln ln 2 ln 32 6 2 3x x x x C− + + + − +
k) Caxa21ax
a21
−++− lnln l) 2ln 5 ln 2x x C+ − − +
m) 12ln 22
+ n) 3ln592ln
527
−
12) a) C4
sen2x2x
+− b) Ccosx3xcos3
+− c) C7xsen
5xsen2
3xsen 753
++−
d) 3 55sen x 3sen x C− + e) 1 1cos8x cos2x C16 4−
+ + f) 5 71 1cos 2x cos 2x C10 14−
+ +
g) 3 515cosx 10cos x 3cos x C− + − + h) 3 51 2 1sen(3 3x) sen (3 3x) sen (3 3x) C3 9 15−
− + − − − +
