Control Deformaciones

TOPOGRAFÍA DE ALTA PRECISIÓN Y CONTROL DE DEFORMACIONES.

1

ASIGNATURA: TOPOGRAFÍA DE ALTA PRECISIÓN Y CONTROL DE DEFORMACIONES.

PROFESOR: DAVID HERNÁNDEZ LÓPEZ. 2ª PARTE: ANÁLISIS DE DEFORMACIONES POR MÉTODOS

GEODÉSICOS. CONTENIDO:

1. INTRODUCCIÓN. 2. DISEÑO DE LA RED DE CONTROL.

3. ANÁLISIS DE DOS ÉPOCAS. 4. ANÁLISIS MULTIÉPOCAS. 5. EJEMPLOS DE APLICACIÓN PRÁCTICA DE ANÁLISIS DE DOS ÉPOCAS.


2

1. INTRODUCCIÓN.

- La teoría del análisis de deformaciones es popular desde la década de los ochenta.

- Las primeras actuaciones se remontan a los años veinte.

- Principales causas de su desarrollo e implantación:

i. La realidad de su necesidad es cada día más evidente.

ii. El avance tecnológico lo posibilita:

1. Desarrollo de instrumental de altas prestaciones. 2. Equipos informáticos muy potentes.

- Su reciente actualidad motiva que todavía se encuentren en desarrollo modelos teóricos que han de intervenir en diferentes fases.

- Aplicaciones actuales:

i. Control de movimientos/deformaciones de obras de ingeniería.

ii. Estudios de deslizamientos de pendientes.

iii. Movimientos corticales.

iv. Evolución de glaciares.

v. Fenómenos de subsidencia.


3

- Objetivo básico:

Analizar la variación en el tiempo de la geometría de un objeto o superficie, o parte del mismo.

- Elementos fundamentales que intervienen.

i. Posible modelo teórico de la evolución geométrica en el tiempo.

ii. Caracterización de la posible variación de la geometría a partir de la modificación de la posición relativa de ciertos puntos singulares.

iii. Necesidad de un marco de referencia respecto al cual medir la variación

geométrica.

iv. Necesidad de medir variación de geometría. Dos métodos básicos:

1. Medición directa. ( inclinómetros, péndulos, extensómetros, ...) 2. A partir de estimación de posiciones o magnitudes geométricas (

ángulos, distancias, incrementos de altitud, ... ) obtenidas en distintos instantes de tiempo comprendidos dentro del intervalo de análisis.

Las medidas son fundamentales además en la definición del marco de referencia.

- Estudiaremos el caso del análisis de deformaciones a partir de las diferentes posiciones encontradas de ciertos puntos singulares del objeto de análisis.

- Consideraremos dos casos generales:

i. Control de obras de ingeniería.

ii. Control de superficies de terreno.


4

- En el control de obras de ingeniería por métodos geodésicos podremos considerar una red de control que incluya a sus puntos agrupados en dos conjuntos:

i. Bloque de referencia. Definirá, junto a los observables el marco de

referencia. Estará integrado por vértices de posición estable en el tiempo. Normalmente se localizarán fuera de la estructura a analizar.

ii. Bloque objeto. Conjunto de puntos a partir de cuya modificación espacial

en el tiempo se obtendrán los resultados de variación geométrica a contrastar con los modelos teóricos, si los hubiera. Su crítica localización es función del modelo de predicción de variación geométrica.


5

- En el control de superficies de terreno únicamente se puede hablar en principio de bloque objeto. Caso del estudio geológico de una zona de terreno separada por una falla que dividiría la red de control en dos subredes, pudiendo determinarse únicamente desplazamientos relativos entre los dos bloques. El desplazamiento relativo pasará por considerar uno de ellos fijo de acuerdo a ciertas hipótesis.


6

- Una fase fundamental del análisis será el diseño de la red, tanto de los vértices incluidos como las observaciones entre ellos.

- El concepto de época de observación hace referencia a cada una de las

campañas de observación repetidas a lo largo del tiempo con un cierto intervalo. - El intervalo entre épocas de observación será función de:

i. Exigencia de detectar ciertas magnitudes de las deformaciones frente al

modelo de evolución de las mismas en el tiempo.

ii. Magnitud de las deformaciones en el tiempo frente a la precisión con la que se consiga su determinación a partir de la red de control, del instrumental y metodología empleados en la observación.

- Teóricamente todas las observaciones de una época se refieren a un instante de

tiempo. Habrá que considerar los problemas asociados a la relación entre la duración de una campaña de observación y las posibles deformaciones producidas durante el tiempo invertido en la misma.

- Los tipos de análisis temporales que se realizan son fundamentalmente de dos

tipos:

i. Análisis dos épocas. Se realizan a partir de dos épocas sucesivas de observación, comenzándose en el momento que se disponga de las dos primeras. La base del análisis son los vectores de deformación.

ii. Análisis multiépoca. Se puede realizar desde el momento en que se

disponga de tres épocas. Aparecen en el análisis velocidades de desplazamiento e incluso aceleraciones del mismo.

- Los métodos geodésicos que se van a describir son una potente herramienta para

investigar la estabilidad de los objetos o superficies analizados. Sin embargo, la fiabilidad de los resultados obtenidos será función de:

i. La calidad del diseño de la red de control.

ii. La calidad del modelo matemático. iii. La calidad de las observaciones.

Cualquier incorrección del modelo: sistematismos no contemplados, errores groseros no detectados, incorrecta evaluación a priori de la precisión de los observables, ... contaminarán el resultado pudiendo incluso dar lugar a estimar deformaciones cuando no las hay.


7

- Los resultados obtenidos en el primer análisis de dos épocas pueden ser

determinantes para introducir modificaciones en el programa del proceso de análisis. Esto sucederá fundamentalmente cuando las deformaciones obtenidas excedan en mucho a las previstas o cuando, por el hecho de no disponer de un modelo de predicción, se concluya que las hipótesis base para el proyecto de análisis eran incorrectas.

Estas modificaciones se pueden referir, principalmente a:

i. Modificación de la localización de los vértices que configuran la Red de Control, siendo dos causas las principales:

1. Inestabilidad de una parte importante del bloque de referencia que

obligue a incluir nuevos vértices en este conjunto o a modificiar la monumentación de los existentes.

2. La localización singular de los puntos del bloque objeto no es

suficiente o correcta para el análisis de la tendencia de movimientos en la estructura. Puede ser que ciertas zonas sufran movimientos cuyo modelo funcional precise de más puntos o de localizaciones distintas a las diseñadas en principio.

ii. Modificación del diseño de la campaña de observación. Normalmente

vendrá motivada por la alteración de la configuración de la Red de Control. También se puede deber a la detección de observaciones prescindibles o, por el contrario, de la conveniencia de nuevas observaciones no diseñadas en principio, motivadas por movimientos previstos que no se producen, o por movimientos producidos y no previstos, respectivamente.

iii. Modificación del intervalo de tiempo transcurrido entre épocas de

observación, debido a que no se cumplen los criterios, ya comentado, con que fue fijado en principio.

- Todos los resultados se obtendrán a partir del modelo Gauss-Markov

convencional. - La definición del sistema de referencia es un grave problema debido a que es

función de la configuración de la red y de los observables, y se verá afectado de los resultados obtenidos a lo largo de todo el análisis.


8

2. DISEÑO DE REDES DE CONTROL DE DEFORMACIONES. 2.1. OBJETIVOS Y VARIABLES.

- Se entiende por diseño de una Red de Control de Deformaciones no solo el diseño de la localización de los vértices que definen su configuración, sino también el diseño de la campaña de observación: observables a medir, instrumental y metodología a emplear.

- Los objetivos de la optimización de una Red de Control de Deformaciones son:

i. Alcanzar una precisión global predeterminada.

ii. Establecer un modelo matemático testeable y real.

iii. Dar sensibilidad suficiente en ciertas funciones conocidas a priori de los

parámetros.

iv. Diseñar una configuración y una campaña de observación viable bajo consideraciones prácticas y económicas.

- La consecución de una precisión global predeterminada estará condicionada de

forma directa con la precisión de los observables, la configuración de la red, el diseño de la campaña de observación y la definición del sistema de referencia. En ningún caso se deberá optar por sistemas de referencia definidos a partir de ciertos constreñimientos que implique pérdida de precisión de los observables. Muy relacionado con el problema del datum se encuentra la pretensión de que las funciones de los parámetros a analizar sean invariantes.

- El segundo objetivo no es otro que la búsqueda de la fiabilidad del modelo.

- El tercer objetivo es fundamental en control de deformaciones dado que una

deformación prevista se puede expresar como una función de los parámetros del modelo. Será crítico que la Red pueda dar respuesta a una deformación de cierta magnitud prevista pues este es el objetivo básico de todo el análisis.


9

- Para conseguir el cuarto objetivo será de gran ayuda contar con un modelo, una cartografía, lo más real posible de la zona de emplazamiento del objeto de análisis, para obtener una primera aproximación. Sin embargo, será imprescindible realizar visitas al lugar con objeto de:

i. Definir el tipo de monumentación o materialización de los vértices de la

Red, que además tendrá un importante peso en el coste del proyecto.

ii. Verificar la intervisibilidad entre los vértices.

iii. Estimar tiempos y dificultades en la realización de cada una de las observaciones de cara a obtener una previsión de coste.

- Las variables que intervienen en el diseño de la Red ya han sido introducidas:

localización de los vértices ( coordenadas aproximadas ), diseño de la campaña de observación ( cada una de las funciones del modelo funcional del GMM ) y la estimación de la precisión de las observaciones, es decir la matriz A de diseño de las incógnitas y la matriz de pesos, P.

- No existe un método matemático que conjugue las variables enunciadas con los

objetivos perseguidos debido a la alta complejidad del problema. Todos los métodos tienen un carácter iterativo.

- Existen dos técnicas básicas para enfrentarse al problema de diseño: a través de

los métodos de simulación y a través de los denominados problemas de diseño. El que se lleva a la práctica habitualmente es el primero.


10

- El proceso de diseño según el método de simulación es iterativo e incluye los siguientes pasos secuenciales:

i. Selección de la ubicación de los vértices con estimación de tipo y coste de

monumentación y sistema de centrado.

ii. Especificar todas las observaciones posibles.

iii. Selección del instrumental y metodología de observación.

iv. Para cada uno de los observables estimar la precisión y coste.

v. Formular el GMM y calcular: medidas de la precisión, fiabilidad y sensibilidad ( funciones objetivo – datum ).

vi. Calcular la influencia de cada observable en las tres medidas del punto v

y en el coste. Ordenar las observaciones a partir de criterios de ordenación establecidos previamente.

vii. Comparar los resultados del paso v con las exigencias de partida y buscar

la solución de mínimo coste cumpliendo los criterios de precisión, fiabilidad y sensibilidad. Esto se consigue realizando:

1. Eliminar algún observable o relajar su método de medida. 2. Contemplar un cambio de instrumentación.

viii. Tras obtener un resultado satisfactorio se puede iterar a partir de otra

localización de los vértices.


11

3. ANÁLISIS DE DOS ÉPOCAS. 3.1. INTRODUCCIÓN.

- El análisis simultáneo de dos épocas sucesivas de observación es de fundamental importancia al ser la fuente más directa de análisis del movimiento producido en el intervalo de tiempo limitado por los instantes correspondientes a cada una de las mismas.

- Normalmente se realiza entre cada dos campañas sucesivas aunque también se

puede realizar cada cierto número de campañas.

- Los principales objetivos de este análisis son:

i. Confirmar la estabilidad de los puntos del bloque de referencia y detectar movimientos singulares, individuales, de puntos que se considerarán como independientes del tiempo no conformando parte del modelo de deformación continua.

ii. Contrastar un modelo de movimientos a partir de los vectores de

deformación, o formular uno en caso de no disponer de uno previsto.

iii. Detectar deformaciones críticas imprevistas de graves consecuencias.

b. Este tipo de análisis suele ser suficiente en muchas aplicaciones.


12

3.2. SEGUNDA FASE. ANÁLISIS DE LOS OBSERVABLES.

- Comenzamos por la segunda fase debido a que suele considerar como primera fase el diseño de la Red de Control. Se ha estudiado aparte dado que no suele cambiar, a no ser que se de alguno de los supuestos considerados anteriormente a partir del análisis de dos épocas.

- Esta fase incluye en completo análisis de los datos geodésicos incluyendo

detección de errores groseros y test globlal del modelo. - Se realiza para cada una de las épocas independientemente.

- La importancia es crucial dado que cualquier error no detectado nos llevaría a

otorgarle una interpretación de deformación.

- Se suele llevar a cabo realizando un ajuste Red Libre minimizando la traza de la matriz cofactor de las incógnitas completa, minimizando la norma de todas las incógnitas, solución pseudoinversa. No se eliminan incógnitas.

- Esta fase se da por completada si se cumple para cada una de las épocas que:

i. No se rechaza el test global del modelo.

ii. No se detectan observaciones con error grosero.

iii. Se verifica que los grupos de observables siguen distribuciones normales.

iv. Se verifica la compatibilidad de grupos de observables.

v. Se verifica la inexistencia de sistematismos en grupos de observables.

- Como posibles causas del rechazo del test global del modelo se pueden citar:

i. En el modelo funcional: Incorrecta reducción y/o proyección de observables, parámetros de calibración de instrumental, campo de la gravedad, refracción, ...

ii. En el modelo estocástico: varianzas a priori, correlaciones, ...

iii. En los observables: errores groseros, errores de centrado, no siguen

distribuciones normales, errores sistemáticos no modelados, ...

iv. En los cálculos: errores de programación, errores de entrada, estabilidad de los métodos numéricos, acumulación de errores de redondeo, ...

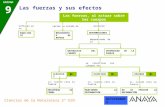
ESQUEMA DE PRIMER Y SEGUNDO PASO DE LA METODOLOGÍA DE ANÁLISIS DE DEFORMACIONES BASADO EN MÉTODOS GEODÉSICOS.

DISEÑO DE LA

RED DE CONTROL.

MODELO GAUSS-MARKOV.

AJUSTE MÍNIMOS CUADRADOS.

PRECISIÓN.

FIABILIDAD.

SENSIBILIDAD.

VIABILIDAD, COSTO.

DISEÑO DE LA CAMPAÑA DE OBSERVACIÓN.

OBSERVABLES. MODELO

GAUSS–MARKOV.

AJUSTE MÍNIMOS

CUADRADOS

TEST GLOBAL DEL MODELO.

DETECCIÓN DE ERRORES GROSEROS.

CONJUNTO DE TEST ESTADÍSTICOS.

PRECISIÓN.

COSTE.

ÉPOCA 1 ÉPOCA 2 ÉPOCA 3

DISEÑO Y VERIFICACIÓN DEL MODELO GAUSS – MARKOV ( GMM )

TEORÍA BASADA EN LA

EXPERIENCIA.

MUNDO REAL

EXPERIMENTOS DE MEDIDA:

OBSERVABLES.

MODELO MATEMÁTICO GAUSS – MARKOV.

MODELO FUNCIONAL.

( ) AxtE =

MODELO ESTOCÁSTICO.

( ) QE T 20σεε =Σ=

CÁLCULO / ESTIMACIÓN - MÍNIMOS CUADRADOS.

PARÁMETROS FUNCIONALES:

( )xfx ˆ ,ˆ

PARÁMETROS ESTOCÁSTICOS.

( )xfxo QQs ˆˆ2 , ,

TESTS ESTADÍSTICOS:

¿ TEORÍA ⇔ REALIDAD ?

RECHAZO.

ACEPTACIÓN.

PROBLEMA DEL DATUM. S-TRANSFORMACIONES.

DEFINICIÓN DEL DATUM POR EL METODO DE LOS CONSTREÑIMIENTOS.

MODELO GMM EXTENDIDO: 0 , =+= xRvtAx t ( ) ( ) rndrAranknmnmMatA −===>ℜ×∈ def.rango , , ,,

Condiciones que se imponen a la matriz R: su rango ha de ser igual al defecto de rango de A y sus columnas deben pertenecer al espacio nulo de A. Conclusión:

( ) ( ) ( ) ( ) 1 −+∃→=+−=+=+ TTTTTT RRPAAnddnRRrankPAArankRRPAArank

SOLUCIÓN GMM EXTENDIDO:

⎟⎟⎠

⎞⎜⎜⎝

⎛⎟⎟⎠

⎞⎜⎜⎝

⎛=⎟⎟

⎠

⎞⎜⎜⎝

⎛⎟⎟⎠

⎞⎜⎜⎝

⎛=⎟⎟

⎠

⎞⎜⎜⎝

⎛−

0000ˆˆ

21

12111

PAAQ

QQPAAR

RPAAx TT

T

T

λ

( ) ( ) 111111

11 , :cumple que , QNNNQRRNNRRNQ TT ∀=++=−−

1111ˆˆ

11ˆNQQQPtAQx

PAAN

xx

T

T

==

=

CONJUNTO DE SOLUCIONES MÍNIMOS CUADRADOS: { } { }PtAQx T11ˆ =

ELECCIÓN DE SOLUCIÓN EN BASE A OPTIMIZAR PRECISIÓN EN UN CONJUNTO DE INCÓGNITAS.

LA SOLUCIÓN QUE OPTIMIZA LA PRECISIÓN EN UN CONJUNTO DE INCÓGNITAS ES AQUELLA QUE MINIMIZA LA TRAZA PARCIAL DE LA MATRIZ COFACTOR DE LAS

INCÓGNITAS CORRESPONDIENTE: ( ) minˆˆ =xxQtrp 1ª SOLUCIÓN: Solución pseudoinversa. Se minimiza la traza total de Qxx. Se consigue con la

elección de: 0 , == ASSR

Obtención de S para redes planimétricas: -Si todas las incógnitas son coordenadas:

⎟⎟⎟⎟⎟

⎠

⎞

⎜⎜⎜⎜⎜

⎝

⎛ −

=

....

....1001

11

11

yxxy

S

Las dos primeras columnas hacen referencia a la traslación, origen (x,y), la tercera a la orientación y la cuarta a la escala. Se factoriza por cholesky: LLSS TT = y se obtiene 1−= SLSn , se consigue

Solución: ( ) Tnn

Tnn SSSSNNQ −+==

−+ 111 y, se demuestra: += NQ xxˆˆ porque la

pseudoinversa cumple: +++ = NNNN - Si aparecen u incógnitas de descentrado al principio,

⎟⎟⎟⎟⎟⎟⎟⎟⎟

⎠

⎞

⎜⎜⎜⎜⎜⎜⎜⎜⎜

⎝

⎛

−−

−

=

....

....1001

0100....0100

11

11

yxxyS

PROBLEMA DEL DATUM. S-TRANSFORMACIONES.

ELECCIÓN DE SOLUCIÓN EN BASE A OPTIMIZAR PRECISIÓN EN UN CONJUNTO DE INCÓGNITAS.

LA SOLUCIÓN QUE OPTIMIZA LA PRECISIÓN EN UN CONJUNTO DE INCÓGNITAS ES AQUELLA QUE MINIMIZA LA TRAZA PARCIAL DE LA MATRIZ COFACTOR DE LAS

INCÓGNITAS CORRESPONDIENTE: ( ) minˆˆ =xxQtrp 2ª SOLUCIÓN: Solución minimizando en más de dos puntos de la red la traza parcial de Qxx,

maximizando la precisión en esos puntos. Se consigue con la elección de:

⎟⎟⎟⎟⎟⎟⎟⎟⎟

⎠

⎞

⎜⎜⎜⎜⎜⎜⎜⎜⎜

⎝

⎛

===

0.

0

0.

0

,0 , kIBASBSR

Con Ik la matriz identidad de tamaño igual al doble del número de puntos y localizada en la posición correspondiente a las incógnitas asociadas a esos puntos.

3ª SOLUCIÓN: Caso solución Red Ligada. Se consigue como caso particular del anterior cuando

del número de puntos es 2. Las incógnitas asociadas a los dos puntos se anulan así como la parte afectada de la matriz cofactor de las incógnitas.

TRANSFORMACIÓN DE UNA SOLUCIÓN A OTRO DATUM. SE BASA EN LA PROPIEDAD: NNNQ =11 , INVARIANTE. SEAN DOS SOLUCIONES DE LA MISMA RED EN DOS DATUM, R1 Y R2.

( ) ( ) 111

111

111

−−++= TT RRNNRRNQ , PERO, NNNQ =2

11 Y ( ) ( ) 111

211

111

111

−−++= TT RRNNNQRRNQ

TENIENDO EN CUENTA LA LEY DE PROPAGACIÓN DE COFACTORES: T

xxyy AAAxy Σ=Σ→=

SE PUEDE INTERPRETAR: 212

1121111 KQKQ = , CON ( ) NRRNK T 1

1121−

+=

LUEGO: ( ) PtANQRRNPtAQKPtAQxKx TTTT 211

111

21121

1112211 ˆˆ −

+==== PUDIÉNDOSE APLICAR DE FORMA RECURSIVA: ( ) 11311223112232233 ˆˆˆˆˆ xKxKKxKKxKx ====

FUNCIONES INVARIANTES FRENTE AL CAMBIO DE DATUM. [ ] xxE ≠ˆ , dado que: [ ] [ ] [ ] NxQPAxAQtPEAQPtAQExE TTT

11111111ˆ ==== ,y, en general, INQ ≠11 Sin embargo, si Bxf = , con TAB = , [ ] [ ] [ ] [ ] fBxTAxNxTAQxTAExTAExBEfE ======= 11ˆˆˆˆ por ser ANAQ =11 un invariante: ANAQPAANPAQANNNQ TT =→=→= 111111 Así, son ejemplos de invariantes: T

xxvvT

xxtt AAQQQtxAvAAQQxAt ˆˆˆˆˆˆˆˆ ,ˆˆ , ,ˆˆ −=−===

CONJUNTO DE TEST ESTADÍSTICOS A LOS QUE SE PUEDE SOMETER EL GMM Y LOS OBSERVABLES.

TEST GLOBAL DEL MODELO. Ho: El modelo es completo y correcto. [ ] 2

020 σ=sE

( )ArankmvPvs

T

−=

ˆˆ20 , estadísto

⎭⎬⎫

⎩⎨⎧= 2

0

20

20

20 ,max s

sq σσ

No se rechaza si ( ) ( ) ∞−−< ,,1 ArankmFq α α es el nivel de significación, o nivel de riesgo, o probabilidad cometer error tipo I.

TEST DE BAARDA DE DETECCIÓN DE ERRORES GROSEROS. Hipótesis de partida: Los residuos están normalmente distribuidos y σ0 es conocido. Ho: La observación i-ésima no presenta error grosero.

Se definen los residuos tipificados: ( )iiQvw

vv

ii ,

ˆˆˆ0σ

=

Bajo Ho, los residuos tipificados wi una distribución ( )1,0N Bajo la hipótesis de un error ∆i, en la observación i-ésima, wi sigue una distribución ( )iwN ∆,0

Siendo: ( )

( )iii

vv

vv

ii ww

iiQiiPiiQ

vw ∆+=∆+=0

ˆˆ

ˆˆ0

,),(,

ˆσσ

Elegidos un α (nivel de significación) y un β ( potencia de test ), de acuerdo al test, una observación es detectada como rechazable si ( )1,0

215.0 α−

> Nwi teniendo en cuenta que:

- hay una probabilidad (1- β) de aceptar una observación con error grosero. - hay una probabilidad α de rechazar una observación sin error grosero.

Normalmente se adoptan: α=0.001 ( con lo que la cota de detección resulta 3.29 ) y β=0.8

CONJUNTO DE TEST ESTADÍSTICOS A LOS QUE SE PUEDE SOMETER EL GMM Y LOS OBSERVABLES.

TEST DE POOPE DE DETECCIÓN DE ERRORES GROSEROS. Hipótesis de partida: Los residuos están normalmente distribuidos pero σ0 no es conocido. Ho: La observación i-ésima no presenta error grosero.

El estadístico a utilizar es: ( )iiQsvT

vv

ii ,

ˆˆˆ0

=

Bajo Ho, Ti sigue una distribución ( )( )Arankm −τ , distribución que se puede obtener a partir de la distribución t-student

( ) ( )

( )2

1

1

1 −

−

+−=

f

f

tf

tffτ

Ho: [ ] { }mivE i ,...2,1 ,0ˆ ∈∀= Ha: Se detecta una observación errónea a través de su residuo. Para un nivel de significación elegido, α, dado que este test consta de m individuos, se determina: un valor aproximado de ( ) m

10 11 αα −−= , nivel de significación de este test m-dimensional.

Ho es rechazado para un residuo k-ésimo si: ( ))(,2 Arankmk oT

−> ατ

TEST DE NORMALIDAD DE LOS RESIDUOS DE GRUPOS DE OBSERVABLES.

Se comienza por agrupar a los observables en función del tipo, instrumental,... y para cada grupo se testea si los residuos estimados de los mismo siguen una distribución normal a través de un test de adherencia. Sea el grupo de residuos k. Se dispone a agruparlos en clases, eligiendo un intervalo de clase adecuado. Sea Ic el intervalo de clase elegido, µ la media y σ2 la varianza del grupo de residuos. La clase que

contiene a la media tendrá por límites del intervalo: ⎥⎦⎤

⎢⎣⎡ +− 2,2

cc II µµ , la siguiente a la derecha

tendrá por límites: ⎥⎦⎤

⎢⎣⎡ ++ 2

3,2cc II µµ , y así sucesivamente. Se procede a calcular la probabilidad

asociada a cada intervalo a partir de tipificar sus extremos. Ho: El grupo de observables sigue una distribución normal.

Se rechaza Ho si ( )

( ) ( )2

1,11

2

−−=

>−∑ k

k

m

m

i ik

iik

pmspm

αχ , con mk el número de residuos del grupo, pi la

probabilidad de cada clase y si el número de elementos de cada clase.

HIPÓTESIS LINEAL GENERAL.

UTILIDAD: PLANTEAR UN TEST PARA VERIFICAR SI LOS PARÁMETROS RESUELTOS SEGÚN GMM VERIFICAN UN CONJUNTO DE CONDICIONES EXPRESADAS LINEALMENTE.

GMM: [ ] ε+== AxtAxtE o

[ ] QE T 20σεε =Σ=

Ho: [ ] 0 o =−= gxHEgxH TT Si no se rechaza Ho, se tendrá que: ( ) HHgNxHg xx

Tgggg

Tˆˆˆˆˆˆ con ,,~ˆˆ Σ=ΣΣ=

y se demuestra que,

( ) ( ) ( )22

0ˆˆ ~ˆˆ HrankggT ggQggq χσ−−= −

∆ y, también,

( )

( )( ) ( )ArankmHrankF

Arankmq

Hrankq

T −

∆

−

= ,~

siendo,

vPvq T ˆˆ=

Ho no se rechazará si se verifica que: ( ) ( ) ( )ArankmHrankFT −−< ,,1 α , para un α elegido.

SOLUCIÓN DEL MODELO SUJETO A LAS RESTRICCIONES.

( ) ( )xHgNHHHNxx TTH ˆˆˆ −+=

−−

( ) ( )( )

( )( ) ( )( ) ( ) ( )0ˆ que ya

ˆˆˆˆˆˆˆˆˆˆˆˆ

ˆˆˆˆˆˆˆˆˆˆ

=

+=−−+=−+−+=

−+=−+−=−=−−=

∆

Av

qqxxNxxvPvxxAvPxxAvq

xxAvxAxAtxAtxAvtxAPtxAq

TH

TH

TH

THH

HHHH

HT

HH

( ) ( ) ( ) ( )( ) ( ) ( )( )( ) ( ) ( )xHgHNHxHg

xHgNHHHNNxHgNHHHNxxNxxqTTTT

TTT

TTH

TH

ˆˆ

ˆˆˆˆˆˆ

−−=

=−−=−−=−−

−−−−∆

( ) ( ) ( ) ( )

( ) ( ) ( )xHgHNHxHgq

HNHQxHg

xHgQxHgqxHgggQggq

TTTT

Tg

T

Tg

TTTg

T

ˆˆ expresiónmisma la Resultando

error de npropagaciópor resulta ˆˆ comoy

ˆˆ luego, ˆˆ pero ˆˆ

ˆ

ˆˆ

−−=

==

−−==−−=

−−∆

−

−∆

−∆

ESQUEMA DE TERCER PASO DE LA METODOLOGÍA DE ANÁLISIS DE DEFORMACIONES BASADO EN MÉTODOS GEODÉSICOS.

ÉPOCA i SISTEMA REFERENCIA:

( ) minˆ =rixQTr

iixoixri fsQxQxoiri

, , ,ˆ, ,ˆ 20ˆˆ

FACTOR DE VARIANZA COMÚN.

fs ,20

TEST DE CONGRUENCIA BLOQUE REFERENCIA.

( ) ( )rjri xExEH ˆˆ :0 =

rirj xxrirj QQQxx ˆˆ ,ˆˆ +=−=∆ ∆

( )∆∆−∆∆ =∆∆= QrankfQq T ,

? F~ ¿ ,20

ffsf

qT

∆

∆

∆

=

BLOQUE REFERENCIA rx

BLOQUE OBJETO ox

ÉPOCA j SISTEMA REFERENCIA:

( ) minˆ =rjxQTr

jjxojxrj fsQxQxojrj

, , ,ˆ, ,ˆ 20ˆˆ

NO SE RECHAZA Ho

EL BLOQUE DE REFERENCIA HA QUEDADO DEFINIDO.

SE RECHAZA Ho

AL MENOS UN PUNTO DEL BLOQUE DE REFERENCIA PRESENTA MOVIMIENTOS

SINGULARES.

Ha : TODOS LOS PUNTOS EXCEPTO UNO DEL BLOQUE DE REFERENCIA SON ESTABLES.

EL PUNTO DE MAYOR CONTRIBUCIÓN A LA

FORMA CUADRÁTICA ∆q SE ELIMINA DEL BLOQUE DE REFERENCIA,

PASÁNDOSE AL BLOQUE OBJETO, Y SE ITERA.

METODOS DE OBTENER q∆ DEL TEST DE CONGRUENCIA DEL BLOQUE REFERENCIA.

TEST DE CONGRUENCIA BLOQUE

REFERENCIA.

( ) ( )rjri xExEH ˆˆ :0 =

rirj xxrirj QQQxx ˆˆ ,ˆˆ +=−=∆ ∆

∆+= qqqH

? F~ ¿ ,20

ffsf

qT

∆

∆

∆

=

METODO 1. MODIFICACIÓN DEL MODELO GMM DEL AJUSTE COMÚN

DE FORMA QUE A LOS PUNTOS A TESTEAR SE LES ASIGNEN UNAS ÚNICAS INCÓGNITAS.

⎟⎟⎠

⎞⎜⎜⎝

⎛+⎟⎟

⎠

⎞⎜⎜⎝

⎛=

⎟⎟⎟

⎠

⎞

⎜⎜⎜

⎝

⎛

⎟⎟⎠

⎞⎜⎜⎝

⎛

j

i

j

i

oj

oi

r

ojrj

oiri

tt

xxx

AAAA

εε

00

RESUELTO EL AJUSTE SE OBTENDRÍAN LOS RESIDUOS TALES QUE:

HHH vPvq ˆˆ= Y SE OBTENDRÍA EL VALOR BUSCADO: qqq H −=∆

METODO 2. APLICANDO LA HIPÓTESIS LINEAL GENERAL.

Ho: ( ) 0=⎟⎟⎠

⎞⎜⎜⎝

⎛−=

rj

riT

xx

IIxH

OBTENIÉNDOSE, DIRECTAMENTE:

( ) ( ) ( )rjrixxxxT

rjri xxQQxxqrjrjriri

ˆˆˆˆ ˆˆˆˆ −+−= −∆

DIAGNOSIS DE PUNTOS SINGULARES.

CONSIDERAREMOS TRES CASOS:

1. TEST DE CONGRUENCIA SINGULAR PARA EL PUNTO. 2. DETECTAR PUNTOS DESPLAZADOS DE UN BLOQUE DE

REFERENCIA CUANDO FALLA EL TEST DE CONGRUENCIA DEL MISMO.

3. DETECTAR PUNTOS DESPLAZADOS DE UN BLOQUE OBJETO CUANDO FALLA EL TEST DE ESTABILIDAD DEL BLOQUE.

LA SOLUCIÓN DEL PRIMERO PASARÍA POR PLANTEAR UN TEST DE CONGRUENCIA SIMILAR AL ANALIZADO PARA EL BLOQUE REFERENCIA.

MOVIMIENTOS SINGULARES EN EL BLOQUE DE REFERENCIA.

Ha: TODOS LOS PUNTOS DEL BLOQUE SALVO UNO SON ESTABLES. HAY QUE DETECTAR EL PUNTO QUE SE HA DESPLAZADO CON MÁS PROBABILIDAD, ELIMINARLO DEL BLOQUE DE REFERENCIA E ITERAR. SE PROCEDE A DETERMINAR LA CONTRIBUCIÓN DE CADA PUNTO A q∆. CONSIDERAREMOS DOS MÉTODOS QUE APORTAN LOS MISMOS RESULTADOS.

DESCOMPOSICIÓN IMPLÍCITA POR LA Ho FORMULADA.

Es un método muy transparente pero exige muchos cálculos. Si qH se obtenía con la imposición de que todos los puntos del bloque eran estables, ahora se determina q’H relajado en el sentido de que se libera de esa condición el punto P cuya contribución se quiere determinar, según el modelo:

⎟⎟⎠

⎞⎜⎜⎝

⎛+⎟⎟⎠

⎞⎜⎜⎝

⎛=

⎟⎟⎟⎟⎟⎟

⎠

⎞

⎜⎜⎜⎜⎜⎜

⎝

⎛

⎟⎟⎠

⎞⎜⎜⎝

⎛

j

i

j

i

oj

Pj

oi

Pi

r

ojPjjr

oiPiir

tt

xxxxx

AAAAAA

εε

0000

donde: rx representa al bloque referencia salvo P.

Resuelto el ajuste se obtendría: HHP qqq '−=∆


MOVIMIENTOS SINGULARES EN EL BLOQUE DE REFERENCIA.

DESCOMPOSICIÓN SUCESIVA DE LA FORMA CUADRÁTICA.

Se puede escribir: ( )∆∆−∆∆ =∆∆= QrankfQq T ,

Con, rjrjriri xxxxrjri QQQxx ˆˆˆˆ ,ˆˆ +=−=∆ ∆ La consideración de que el punto P se ha movido mientras que el resto son estables nos lleva a plantear una consideración a bloques,

−

∆−∆ ⎟⎟

⎠

⎞⎜⎜⎝

⎛=⎟⎟

⎠

⎞⎜⎜⎝

⎛==⎟⎟

⎠

⎞⎜⎜⎝

⎛∆∆

=∆PPPN

NPNN

PPPN

NPNN

P

N

QQQQ

PPPP

PQ ,

Descomponemos la forma cuadrática en dos subformas estocásticamente independientes por transformación de ∆. Esto se realiza de forma que los subvectores resultantes, uno referido a P y el otro al resto de los puntos, resulten ortogonales. La transformación será:

⎟⎟⎠

⎞⎜⎜⎝

⎛∆∆

=∆⎟⎟⎠

⎞⎜⎜⎝

⎛=∆ −

P

N

PNPP IPPI

1

0

Se demuestra que: −− −= NNPNPNPP QQPP 1

Comprobándose que:

⎟⎟⎠

⎞⎜⎜⎝

⎛−

=⎟⎟⎠

⎞⎜⎜⎝

⎛−⎟⎟

⎠

⎞⎜⎜⎝

⎛⎟⎟⎠

⎞⎜⎜⎝

⎛−

= −−−∆NPNNPNPP

NNT

NNPNPPPN

NPNN

NNPN QQQQQ

IQQI

QQQQ

IQQI

Q0

000

Resultando la descomposición,

( ) PNPNNPNPPTPNNN

TN

T QQQQQQ ∆−∆+∆∆=∆∆−−−−

∆

1

Pero, se demuestra que: NPNNPNPPPP QQQQP −− −=1 Y, finalmente,

PN

PPPTPNNN

TN

T

qqq

PQQ

∆∆∆

−−∆

+=

∆∆+∆∆=∆∆


ELIPSE DE DEFORMACIÓN.

MOVIMIENTOS SINGULARES EN EL BLOQUE OBJETO.

De acuerdo al método de descomposición sucesiva de la forma cuadrática, se obtiene para cada

punto del bloque objeto su contribución iPq∆ . Se plantea el siguiente test para verificar el desplazamiento de cada punto. Ho: El punto Pi es estable. Se rechaza Ho para un nivel de significación elegido si,

( ) f

P

Ff

q

qT

i

,2,12

α−

∆

>=

Una aproximación gráfica al problema anterior se consigue si se dibuja la elipse de deformación junto al vector de deformación. Si el extremo del vector cae fuera de la elipse de confianza ( para un 95%, equivalente a un 0.05 de α anterior ) se dice que el punto es inestable. La elipse de deformación se obtiene de la forma cuadrática bidimensional:

∆∆=∆ PPTP

P Pq i

Si, por correspondencia por las elipses de error, denominamos: 1−= xxPP QP Los parámetros de la elipse de error se obtendrán según:

Y la elipse de confianza resultará de aplicar un factor a los semiejes definido por:

( ) fFsm ,2,10 2 α−=

( )( )

( )

( )yyxx

xy

yxxyyyxx

yyxx

yyxx

qqq

qqqqz

zqq

zqq

−=

+−=

−+=

++=

22tan

42

12

1

22

2

1

α

λ

λ

⎟⎟⎠

⎞⎜⎜⎝

⎛=

yyyx

xyxxxx qq

qqQ

ESQUEMA DEL CUARTO PASO DE LA METODOLOGÍA DE ANÁLISIS DE DEFORMACIONES BASADO EN MÉTODOS

GEODÉSICOS. NO SE RECHAZA LA Ho DEL TEST DE

CONGRUENCIA DEL BLOQUE REFERENCIA: LOS PUNTOS DEL BLOQUE REFERENCIA

DEFINEN UN BUEN SISTEMA DE REFERENCIA PARA ANALIZAR LAS

DEFORMACIONES DE LOS PUNTOS DEL BLOQUE OBJETO.

SE PROCEDE A UNIFICAR LAS DOS ÉPOCAS REALIZANDO UNA NUEVA COMPENSACIÓN CONJUNTA CONSIDERANDO UNAS ÚNICAS

INCÓGNITAS PARA LOS PUNTOS DEL BLOQUE REFERENCIA ENCONTRADO O SE

APLICAN S-TRANSFORMACIONES. EN LA NUEVA SOLUCIÓN SE MINIMIZA LA

TRAZA PARCIAL DE LA MATRIZ COFACTOR DE LAS INCÓGNITAS EN EL BLOQUE

REFERNCIA ENCONTRADO.

LOS VECTORES DE DEFORMACIÓN DE LOS PUNTOS DEL BLOQUE OBJETO SERÁN LAS DIFERENCIAS ENTRE SUS PARES DE

COORDENADAS DEL AJUSTE ANTERIOR. A PARTIR DE LOS MISMOS SE REALIZA EL SIGUIENTE ANÁLISIS:

ANÁLISIS DE PUNTOS SINGULARES SOBRE LA FORMA CUADRÁTICA:

( )∆∆

−∆∆ =∆∆= QrankfQq T ,1

oiojojoiojojoioi xxxxxxxxojoi QQQQQxx ˆˆˆˆˆˆˆˆ ,ˆˆ −−+=−=∆ ∆

ESQUEMA DEL QUINTO PASO DE LA METODOLOGÍA DE ANÁLISIS DE DEFORMACIONES BASADO EN MÉTODOS

GEODÉSICOS.

TEST DE ESTABILIDAD DE LOS PUNTOS DEL BLOQUE OBJETO.

Ho: Los puntos son estables, no hay deformación. Se rechaza para un nivel de significación elegido si:

( ) F ,,120

ffsf

qT

∆−∆

∆

>= α

Siendo ∆f el doble del número de puntos del bloque objeto. 20s el calculado en el ajuste del paso cuarto.

A PARTIR DEL RESULTADO DEL TEST NOS PLANTEAMOS:

NO SE RECHAZA EL TEST. NO EXISTEN DEFORMACIONES.

TALVEZ SEA PRECISO

INCREMENTAR EL INTERVALO DE TIEMPO ENTRE ÉPOCAS, O MEJORAR EL INSTRUMENTAL.

SE RECHAZA EL TEST. EXISTEN DEFORMACIONES.

HABRÁ QUE PROCEDER A

ESTUDIAR DISTINTAS POSIBILIDADES.

ÚNICAMENTE APARECEN

DEFORMACIONES SINGULARES EN

PUNTOS. LA DEFORMACIÓN NO

RESPONDE A UN MODELO.

ESTO SE AVERIGUA PLANTEANDO EL

TEST DE MOVIMIENTOS

SINGULARES EN EL BLOQUE OBJETO.

TODOS LOS PUNTOS

PRESENTAN DEFORMACIONES.

DEFORMACIÓN TIPO SÓLIDO RÍGIDO.

DEFORMACIÓN SEGÚN ALGÚN MODELO

CONOCIDO.

DEFORMACIÓN SEGÚN FUNCIÓN POLINÓMICA.

DEFORMACIÓN TIPO DISTORSIÓN HOMOGÉNEA.

DEFORMACIÓN A MODELAR.

..............

ESTUDIO DE UN DETERMINADO MODELO DE DEFORMACIÓN SOBRE LOS VECTORES DE DEFORMACIÓN DEL BLOQUE

OBJETO.

DATOS DE PARTIDA Y ESTIMACIÓN MÍNIMOS CUADRADOS:

A partir del ajuste común de las dos épocas comentado anteriormente disponemos de:

- vector de deformación de los puntos del bloque objeto, que será el vector de observables, - y de su matriz varianza-covarianza, que será la de los observables.

EL modelo de deformación se escribirá en general:

[ ] [ ] ( )∆∆∆ →=Σ==

+∆=

QsNQsEEBp

T 20

20 ,0~ , ,0

,εεεε

ε

donde:

ojoi xx ˆˆ −=∆ , es el vector de deformación de los puntos objeto.

oiojojoiojojoioi xxxxxxxx QQQQQ ˆˆˆˆˆˆˆˆ −−+=∆ , su matriz cofactor.

20s , es la estimación de la varianza a aposteriori del ajuste común.

B , es la matriz de diseño del modelo planteado. p , es el vector de parámetros del modelo.

Estimación mínimos cuadrados:

( )( )

( )

npnptoQs

BBQBBQQ

pB

BQBQ

QBBQBp

T

TT

Tpp

TT

−=

−=

∆−=

=

∆=

−∆

−−∆∆

−−∆

−∆

−−∆

2ˆ

ˆ

ˆ

120

11

11ˆˆ

111

δδ

δ

δδ

donde, 2npto es el número de ecuaciones, y np es el número de parámetros. También se deberán estimar: residuos tipificados, mínimo error detectable, números de redundancia, ...

ESTUDIO DE UN DETERMINADO MODELO DE DEFORMACIÓN SOBRE LOS VECTORES DE DEFORMACIÓN DEL BLOQUE

OBJETO.

TEST ESTADÍSTICOS A LOS QUE SE SOMETE EL MODELO.

1. TEST GLOBAL DEL MODELO. Ho: El modelo es congruente con la deformación a estudiar. Se rechaza Ho si para un nivel de significación elegido,

( ) ff pFs

ss

s,,12

0

20

20

20

ˆ,ˆmax α−>⎭⎬⎫

⎩⎨⎧

donde fp son los grados de libertad del modelo.

2. TEST DE SIGNIFICANCIA DE LOS PARÁMETROS. Ho: Los parámetros del modelo no son significativos. Se rechaza Ho si para un nivel de significación elegido,

( ) fnp

p

Tp

Fsnp

q

T

pQpqpp

,,120

ˆ

1ˆ

ˆ

ˆˆˆˆ

α−

−

>=

=

donde np es el número de parámetros del modelo.

3. TEST DE SIGNIFICANCIA DE LOS RESIDUOS DEL MODELO. Ho: Los residuos de las deformaciones no son significativos. Se rechaza Ho si para un nivel de significación elegido,

( ) ffp

T

pF

sf

q

T

Qq

,,120

1

ˆ α

δ

δδδ δδ

−

−

>=

=

donde fp son los grados de libertad del modelo.

MODELO DE DEFORMACIÓN DE CUERPO ELÁSTICO SUJETO A ESFUERZOS.

FUNDAMENTOS DE ESTE MODELO. SE ENCUENTRAN EN LA TEORÍA DE ELASTICIDAD APLICADA A CUERPOS ELÁSTICOS QUE SE ENCUENTRAN SOMETIDOS A ESFUERZOS, EN LA MECÁNICA DE MEDIOS ELÁSTICOS. ESTE ESTUDIO CENTRADO EN LA TIERRA CONSTITUYE UNO DE LOS OBJETIVOS BÁSICOS DE LA SISMOLOGÍA. PARA UN MEDIO ELÁSTICO PERFECTO, LA LEY DE HOOKE ESTABLECE QUE LAS DEFORMACIONES SON PROPORCIONALES A LOS ESFUERZOS. AL SER LA DEFORMACIÓN CONTINUA POR DEFINICIÓN, EL MODELO SE PODRÍA EXPRESAR COMO: tFxx +=' , SIENDO F CONTINUA Y t UNA POSIBLE TRASLACIÓN CONTEMPLADA. LA LINEALIDAD DE LA EXPRESIÓN SE CORRESPONDE CON LA LEY DE HOOKE Y PLANTEA ADEMÁS UNA HOMOGENEIDAD QUE PUEDE NO AJUSTARSE A LA REALIDAD POR LO QUE PUEDE SER PRECISO PLANTEAR EL PROBLEMA EN EL MARCO DE LOS ELEMENTOS FINITOS, CONSIDERANDO LA LINEALIDAD EN CIERTAS REGIONES LIMITADAS POR FALLAS, FRACTURAS, ... LA APLICACIÓN MÁS DIRECTA SERÁ A ESTUDIOS DE DEFORMACIONES DE LA CORTEZA TERRESTRE, DE MOVIMIENTO DE TIERRAS, DE DESLIZAMIENTO DE LADERAS, ... ADMITIREMOS QUE LAS DEFORMACIONES SON PEQUEÑAS, DE ACUERDO A LA MAGNITUD DE LOS PARÁMETROS ELÁSTICOS DE LA TIERRA APORTADOS POR LA SISMOLOGÍA Y GEOFÍSICA. IDENTIFICAREMOS LOS PARÁMETROS QUE DEFINEN ESTE MODELO CON LOS PARÁMETROS DE UNA TRANSFORMACIÓN AFÍN QUE PERMITE OBTENER LA GEOMETRÍA DEL CUERPO DEFORMADO A PARTIR DE LA GEOMETRÍA ORIGINAL. CONSIDERAREMOS UN MODELO COMPUESTO POR UNA DEFORMACIÓN TIPO SÓLIDO RÍGIDO Y POR UNA DISTORSIÓN. LA PRIMERA PODRÁ DEBERSE A UNA ROTACIÓN Y UNA TRASLACIÓN QUE PRODUCIRÁ UN DESPLAZAMIENTO EN EL CUERPO PERO NO LO DISTORSIONARÁ. SE ESTUDIARÁ QUE LOS PARÁMETROS DE LA DEFORMACIÓN SE PUEDEN OBTENER A PARTIR DE MEDICIONES GEODÉSICAS POR DOS CAMINOS DISTINTOS:

- A TRAVÉS DE LA DIFERENCIA EN LA POSICIÓN DE UN CONJUNTO DE PUNTOS SINGULARES REPRESENTATIVOS DE LA DEFORMACIÓN DEL CUERPO PARTICULAR.

- A PARTIR DE DIFERENCIAS ENTRE OBSERVACIONES GEODÉSICAS REALIZADAS ENTRE ESOS PUNTOS ANTES Y DESPUÉS DE LA DEFORMACIÓN.

SE EXPONDRÁN DISTINTOS PARÁMETROS PARA EXPRESAR LA DEFORMACIÓN: MATRIZ DE DEFORMACIÓN, TENSOR DE DISTORSIÓN, TENSOR DE ESFUERZOS, ROTACIÓN, TENSOR DE CAUCHY, TENSOR DE GREEN, TENSOR DE DISTORSIÓN PURA, EXTENSIÓN DE LÍNEA, ELONGACIÓN CUADRÁTICA, FACTOR DE ESCALA, ...

MODELO DE DEFORMACIÓN DE CUERPO ELÁSTICO SOMETIDO A ESFUERZOS.

PARÁMETROS DEL MODELO.

MODELO: dFIdfffdf

ffff

yy

xy

yx

xx

FtFxxyyyx

xyxx

yyyx

xyxx +=⎟⎟⎠

⎞⎜⎜⎝

⎛+

+=⎟⎟

⎠

⎞⎜⎜⎝

⎛=

⎟⎟⎟

⎠

⎞

⎜⎜⎜

⎝

⎛

∂∂

∂∂

∂∂

∂∂

=+=1

1''

'' ,' , t traslación.

⎟⎟⎠

⎞⎜⎜⎝

⎛==⎟⎟

⎠

⎞⎜⎜⎝

⎛=

yyyx

xyxx

yyyx

xyxx

eeee

Edfffdf

dF

F es la denominada matriz de deformación, dF, o E, es el tensor de deformación. INTERPRETACIÓN GEOMÉTRICA DIRECTA, PRESCINDIENDO DE LA TRASLACIÓN:

( )( ) xtgydfy

ytgxdfx

yy

xx

⋅++=⋅++=

βα

1'1'

siendo: ( )xxdf+1 Factor de escala aplicado en el eje x origen. ( )yydf+1 Factor de escala aplicado en el eje y origen. α, β Ángulos de compresión de los ejes y, x originales, respectivamente. MODELO INTRODUCIENDO EL VECTOR DESPLAZAMIENTO:

Edfffdf

FtdFxdxyyyx

xyxx =⎟⎟⎠

⎞⎜⎜⎝

⎛=+= d ,

F en general no es simétrica pero dado que es de rango completo se puede factorizar en la forma:

⎟⎟⎠

⎞⎜⎜⎝

⎛⎟⎟⎠

⎞⎜⎜⎝

⎛−

==yyxy

xyxx

VVVV

VRFωωωω

cossinsincos

* siendo R una matriz de rotación y V la matriz de distorsión.

La simetría de V permite encontrar una expresión para la rotación: yyxx

yxxyT

ffff

tgFRV+

−=→= ω

Se introducen los tensores de Cauchy, C, y Green, G: ( ) GIVVICGVVFFC TTT 221 , +=→−===

La descomposición en autovalores y autovectores de V dará los módulos de deformación máximo y mínimo, tensiones principales, así como sus orientaciones, dando la elipse de tensión:

( ) ( )

( )yyxx

xyxyyyxx

yyxxyyxx

VVV

tgVVVaux

auxVVemauxVVem

−=+−=

−+=+==++=+==

22 ,4

211 ,2

11

22

222111

θ

λλ

Otros parámetros de interés:

yyxx

xy

CCC

='cosϕ , ángulo que formarán los ejes x, y , deformados.

( )2' ,'s

sqssse =−= , extensión de línea y elongación cuadrática.

( ) tsenCtsentCtCtq yyxyxx22 cos2cos ++= , elongación cuadrática dirección t con eje x origen, directo.

( )⎟⎟⎠

⎞⎜⎜⎝

⎛ −+−=

xFdxddxdyffdyfdxf

atgdt Txxyyxyyx

22

, variación que experimenta una dirección.

21 ,1' ,' λλ=+==−

= AA mdAAAm

AAAdA , dilatación superficial y módulo de dilatación superficial.

MODELO DE DEFORMACIÓN DE CUERPO ELÁSTICO SOMETIDO A ESFUERZOS.

SIMPLIFICACIÓN DEL MODELO: DEFORMACIÓN INFINITESIMAL.

Si la deformación es infinitesimal, IG << , retomando

( ) GIVVVVCICG TT 2 ,21 +=→=−=

se deduce que, V se puede aproximar por la suma de I y G, ya que 0→GGT ( ) ( ) GIGGGIGIGIVVGIV TTT 22 +≈++=++=→+=

despreciando términos de segundo orden.

Se escribe: ε+=+= IGIV ii , siendo ε el tensor de esfuerzos: ⎟⎟⎠

⎞⎜⎜⎝

⎛=

yyyx

xyxx

εεεε

ε

Se puede obtener de: ( ) ( ) ( )( )( ) ( )TTTT dFdFIdFIdFIIFFIVVG +≈−++=−=−== 2

12

12

12

1ε

( ) ( ) ( )( ) ⎟

⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+=+=+=

yyyxxy

yxxyxxTT

eee

eeeEEdFdF

21

21

21

21ε

despreciando términos de segundo orden. En cuanto a la rotación, al ser el ángulo infinitesimal, ii dRIR += Considerando: ( ) ( ) εεεε +=++=+=+== iiiiiiii RdRIRRRIRVRF , despreciando términos de segundo orden, y considerando también, εε +=−+=−= ii dRIRIFdF , finalmente,

( ) ( ) ( )TTTii FFdFdFIdFdFdFIEdFIdRIR −=−+=+−+=−+=+= 2

12

12

1

( ) ( ) ( ) ( )( ) ( )yxxy

xyyx

yxxyTTi eew

ee

eeEEdFdFwdR −=→

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−=−=−= 2

102

12

102

12

1

siendo directo que, ( ) ( ) i

TT dREEEEEdF +=−++== ε21

21

Control Deformaciones

Documents

Transcript of Control Deformaciones