cursoactuairalesii_2013-1
-
Upload
jorge-ramos -
Category
Documents
-
view
50 -
download
0
Transcript of cursoactuairalesii_2013-1

1
Curso de Matemáticas Actuariales del
Seguro de Personas II
(SEMESTRE 2013-1)
Prof.: José Fernando Soriano Flores Email: [email protected] (Messenger) Tel Movil: 55-21064804 Tel Oficina: 91577400 Ext. 2122
Prof. Adjunto: Christian Arturo Quiroga V. Email: [email protected] TEMARIO GENERAL:
1. Repaso de Matemáticas Actuariales del Seguro de Personas I 2. Asset Share 3. Probabilidades para Vida Conjunta y último Sobreviviente 4. Anualidades para Vida Conjunta y último Sobreviviente 5. Primas Netas para Vida Conjunta y último Sobreviviente 6. Ley de Mortalidad Gompertz-Makeham 7. Tabla de Decrementos Múltiples. 8. Modelos Contingentes de Vida Bajo el Caso Continuo
(no incluido en este material)
FORMA DE CALIFICAR:
• EXAMENES 60% • TAREAS 40% • ASISTENCIA 10%
INTRODUCCIÓN: El curso será teórico-práctico y efectivo se verán a profundidad los temas conforme sean requerido en el temario para que su comprensión sea del 100% y considerar todo el temario de estudios. CONSIDEREACIONES: El curso ahora cuenta con modelos de vida, bajo enfoque continuo. La bibliografía correspondiente es el libro Actuarial Mathematics, Bowers, ACTEX. Para el desarrollo del curso que compete al enfoque discreto, se han preparado estas notas de clase en formato PDF con el contenido de todo lo que se verá en el semestre, la finalidad de estas notas es que el alumno no anote ni tome apuntes en clase, simplemente pondrá atención a la clase y si cree conveniente anotar algo lo hará sobre las mismas notas ya impresas. Además se cuenta con un nuevo blog del curso: actuarialestarea.wordpress.com Este blog contendrá de manera permanente el material de clase a lo largo del semestre 1.- Repaso de Matemáticas Actuariales del Seguro de Personas 1. 1.1 Tabla de Mortalidad Definición: Una Tabla de Mortalidad es un Cuadro Estadístico que resume el impacto de la mortalidad en un grupo cerrado de personas (Cohorte Generalmente Ficticia) denotado como
xl . Clasificación:
• Generada o de Cohorte: Se construye en base a la observación de un grupo cerrado de personas hasta que dicho grupo desaparezca por la causa de muerte
• Actual: Se construye en un periodo corto de tiempo tomando como referencia dos censos o observaciones
Tipos:
• Abreviada: Como su nombre lo indica es una tabla abreviada la cual emplea grupos de edad resumidos generalmente las edades 1, 4, 5, 10, 15, 20, etc.
• Completa: Utiliza edades completas (1, 2, 3, 4, 5, 6, 7, 8, etc.)

2
Construcción: Para construir una tabla de Mortalidad es necesario hacer uso de la siguiente notación:
• xl : Número de Vivos de Edad exacta x
• xd : Número de muertes ocurridas entre las edades x y x+1, es decir:
1+−= xxx lld
• xn d : Número de muertes ocurridas entre las edades x y x+n, es decir:
nxxxn lld +−=
• xp : Probabilidad de que una persona de edad x sobreviva 1 año más, es decir:
{ }{ }TotalesCasos
FaborablesCasosll
px
xx
1+=
• xn p : Probabilidad de que una persona de edad x sobreviva n años más
x
nxxn llp +=
• xq : Probabilidad de que una persona de edad x muera entre las edades x y x+1
{{ }
}TotalesCasos
FaborablesCasosld
qx
xx =
Es decir:
xx
x
x
xx
x
xx p
ll
lll
ldq −=−=
−== ++ 11 11
• xn L : Años persona vividos entre las edades x y x+n.
Esta es una de las series más importantes de una tabla de mortalidad y generalmente es la que menos se entiende, su comprensión y estimación se vuelve esencial para poder comprender muchos tópicos actuariales, con el fin de que se entienda cuál es la interpretación de los Años-Persona Vividos considérese el siguiente ejemplo: Supongamos que tenemos un grupo de tres personas todas de edad 25, y supongamos también que una de ellas llega con vida a la edad 30, otra a la edad 29 y otra a la edad 28,
eso quiere decir que una persona vivió 5 años entre las edades 25 y 30, otra vivió 4 años entre las edades 25 y 30, y otra vivió 3 años entre las edades 25 y 30, esto quiere decir que los años persona vividos entre las edades 25 y 30 fueron de 5+4+3=12 años. Dado el ejemplo anterior podemos decir que los años persona vividos entre las edades x y x+n es el área bajo la función lx como se muestra en la siguiente figura:
En el caso de conocer la función lx de manera continua entonces diríamos que:
dxlLnx
xxxn ∫
+
=
Como desconocemos dicha función entonces suponemos que la función lx se comporta de manera lineal entre las edades x y x+n, de tal manera que el área a calcular es de un rectángulo cuya base mide n y altura lx+n, y un triangulo de base n y altura lx – lx+n, de tal manera que:
( ) ( ) [ ]nxxdEMOSTRARTAREA
nxxnxxn llnllnlnL +++ +=−+=22
(TAREA 1. DEMOSTRAR ULTIMA IGUALDAD)
• xL : Años persona vividos entre las edades x y x+1
[ ]121
++= xxx llL
• xT : Años persona vividos entre las edades x y w
∑=
=w
xttnx LL

3
• xe : Esperanza de vida a la edad x (Número de años que se espera viva una persona
de edad x:
x
xx lTe =
En términos generales se puede decir que estas son todas las funciones que componen una tabla de mortalidad, sin en cambio, el actuario para hacer cálculos financieros se apoya en funciones adicionales llamados “Valores Conmutados” Valores Conmutados.
• xx
x lVD ⋅=: Donde ( ) xx iV −+= 1 e i = Interés Técnico
• ∑=
=w
xttx DN :
• xx
x dVC ⋅= +1:
• ∑=
=w
xttx CM :
(TAREA 2. Calcular una tabla de mortalidad en base a la serie lx y un interés técnico del 5%)
1.2.- Anualidades Contingentes. En el curso de matemáticas financieras se estudio este tema como “Anualidades Ciertas”, y consistía en una serie de pagos “ciertos”, en el caso de Matemáticas Actuariales I se estudia este tema como Anualidades “contingentes” que consisten en una serie de pagos que dependen de una contingencia, es decir, la serie de pagos va a depender directamente de la ocurrencia de una contingencia, en nuestro caso, va a depender de si vive o muere la persona.
xn E Dotal Puro n años: En este caso se dará un solo pago de 1 u.m. (unidad monetaria) a una persona de edad x si esta llega con vida a la edad x+n, es decir, sobrevive n años, este valor presente se calcula de la siguiente manera:
x
nx
xx
nxnx
x
nxnx
x
xnn
xn DD
lVlV
llV
VVPVE ++
++ =
⋅
⋅=⎟⎟
⎠
⎞⎜⎜⎝
⎛⋅=⋅⋅= 1
xa Anualidad Vitalicia Vencida: Supongamos ahora que se va a dar un pago de 1 u.m. al final del año de forma anual a una persona, siempre y cuando esta permanezca con vida, este
valor presente se calcula de la siguiente manera:
x
x
x
w
ttx
x
w
x
x
x
xxxwxxx D
ND
D
DD
DD
DDEEEa 1121
21+=
+++
− ==++=+++=∑
xa Anualidad Vitalicia Anticipada: Supongamos ahora que se va a dar un pago de 1 u.m. al principio del año de forma anual a una persona, siempre y cuando esta permanezca con vida, este valor presente se calcula de la siguiente manera:
x
xx D
Na =
nxa : Anualidad Vencida Temporal n años: Supongamos ahora que se va a dar un pago de 1 u.m. al final del año de forma anual durante n años, a una persona siempre y cuando esta permanezca con vida, este valor presente se calcula:
x
w
nttx
w
ttx
x
nx
x
x
x
xxnxxnx D
DD
DD
DD
DDEEEa
∑∑+=
+=
++++
−=++=+++= 1121
21:
Es decir:
x
nxxnx D
NNa 11:
+++ −=
nxa : Anualidad Anticipada Temporal n años: Supongamos ahora que se va a dar un pago de 1 u.m. al principio de cada año de forma anual durante n años, a una persona siempre y cuando esta permanezca con vida, este valor presente se calcula, análogamente a lo anterior de la siguiente manera:
x
nxxnx D
NNa +−
=:
Hasta ahora se han analizados los casos en los que se entrega una cantidad de unidades monetarias si una persona llega con vida, o vive determinado numero de años. Toca tiempo de analizar aquellos casos en los que se entregara una cantidad de unidades monetarias si la persona muere en un número determinado de años, a este tipo de casos se les llama “Seguros”.

4
.2.- Seguros
xA Seguro Ordinario de Vida: Una persona de edad x, contrata un seguro ordinario de vida, y así en caso de que fallezca, se le entregara una suma asegurada de 1 u.m. a los beneficiarios en cuanto la persona fallezca. Este valor presente se calcula de la siguiente manera:
x
x
x
w
xtt
x
x
x
x
xx
xx
xx
xx
x
x
x
xx
x
x
x
x
xx
DM
D
C
DC
DC
lVdV
lVdV
ldV
ldV
VV
ldV
ldVA
==++=+⋅
⋅+
⋅
⋅=
=⎟⎟⎠
⎞⎜⎜⎝
⎛+
⋅+
⋅=+
⋅+
⋅=
∑=++
++
++
1121
12
12
nxA : Seguro Temporal n años: Una persona de edad x, contrata un seguro de vida, y así en caso de que fallezca antes de los próximos n años, se le entregara una suma asegurada de 1 u.m. a los beneficiarios en cuanto la persona fallezca. Este valor presente se calcula de la siguiente manera:
x
nxx
x
w
nxtt
w
xtt
x
nx
x
x
x
x
xx
nxnx
xx
xx
xx
xx
x
nxn
x
x
x
xx
x
x
nxn
x
x
x
xnx
DMM
D
CC
DC
DC
DC
lVdV
lVdV
lVdV
ldV
ldV
ldV
VV
ldV
ldV
ldV
A
++==
−++−++
+++
−++−++
−=
−=
+++=⋅
⋅+
⋅
⋅+
⋅
⋅=
⎟⎟⎠
⎞⎜⎜⎝
⎛ ⋅++
⋅+
⋅=
⋅+
⋅+
⋅=
∑∑
111121
112
112
:
nxA :: Seguro Dotal Mixto n años: Una persona de edad x, contrata un seguro de vida Dotal Mixto, y así en caso de que fallezca antes de los próximos n años ó llegue con vida, se le entregara una suma asegurada de 1 u.m. a el o a los beneficiarios. Este valor presente se calcula de la siguiente manera:
x
nxnxxnxxnnx D
DMMAEA ++ +−
=+= :::
1.3.PRIMAS En términos Generales ya se vio este tema, pues el ultimo tema que vimos fue el de “seguros” denotado en general con una “A”, y dado que es un valor presente, también lo podemos ver como una “prima neta única”, es decir, a el valor presente de un seguro, se puede ver como una prima que se pagara en una sola exhibición para cubrir el siniestro (fallecimiento), pero que pasa si el asegurado no quiere pagar en una sola exhibición el seguro. Entonces se desprende la siguiente formula general para calcular una Prima Neta Nivelada: PRIMA NETA NIVELADA En este caso el asegurado pagara una prima “P” de manera anual y siempre de la misma cantidad durante la vigencia del seguro, de tal manera que se tiene que cumplir:
AaP =⋅ Es decir, que la prima P (Serie de pagos periódicos iguales) traída a valor presente debe de ser igual a la prima que se pagaría en una sola exhibición y finalmente la formula general quedaría:
aAP
=
xP Prima Neta Nivelada para un seguro Ordinario de Vida: Usando la formula general tenemos que:
x
x
x
x
x
x
x
xx N
M
DNDM
aA
P ===
nxP : Prima Neta Nivelada para un seguro Temporal n años: Usando la formula general tenemos que:
nxx
nxx
x
nxx
x
nxx
nx
nxnx NN
MM
DNNDMM
aA
P+
+
+
+
−
−=
−
−
==:
::

5
(Tarea 3: Calcular la formula para calcular la prima neta nivelada para un Seguro Dotal Mixto) 1.4 Reservas: Sean:
• tVPOC = Valor Presente de las obligaciones de la compañía en el año t.
• tVPOA = Valor Presente de las obligaciones del asegurado en el año t.
Entonces la formula general para calcular una reserva en el año t sería:
[ ]ttt VPOAVPOCV −= Por ejemplo:
xtV Reserva al año t de un seguro Ordinario de Vida contratado a edad x: Usando la formula general antes vista tenemos que:
[ ]txxtxtx
tx
txx
tx
tx
VPOA
txx
VPOC
txxt
NPMASD
DN
PDM
ASaPAASVtt
+++
+
+
+
+++
⋅−⋅=
⎥⎦
⎤⎢⎣
⎡⎟⎟⎠
⎞⎜⎜⎝
⎛−⎟⎟⎠
⎞⎜⎜⎝
⎛=⎥⎥
⎦
⎤
⎢⎢
⎣
⎡⋅−⋅=
..1
....
nxtV : Reserva al año t de un seguro temporal n años contratado a edad x: Nuevamente usando la formula general antes vista tenemos que:
( ) ( )[ ]nxtxnxnxtxtx
tx
nxtxx
tx
nxtx
VPOA
tntxnx
VPOC
tntxnxt
NNPMMASD
DNNP
DMMAS
aPAASVtt
+++++
+
++
+
++
−+−+
−−−=
⎥⎦
⎤⎢⎣
⎡⎟⎟⎠
⎞⎜⎜⎝
⎛ −−⎟⎟⎠
⎞⎜⎜⎝
⎛ −=
⎥⎥
⎦
⎤
⎢⎢
⎣
⎡⋅−⋅=
:
::::
..1
..
..
(Tarea 4.- Calcular la formula para calcular la reserva al año t de un seguro Dotal Mixto contratado a edad x)
Para aplicar en la práctica lo visto en este repaso el siguiente tema es: 2. ASSET SHARE: Se pueden encontrar muchas definiciones de Asset Share e incluso la traducción al castellano es algo ambigua pero, para efectos de este curso lo definiremos como: la simulación de la rentabilidad que se espera tener por la venta de un seguro .En este caso, un seguro de vida, para simular dicha rentabilidad nos apoyaremos de la teoría actuarial que ya vimos y en una hoja de cálculo de Excel, de tal manera que la finalidad de este ejercicio nos ayudara a dominar esta herramienta tan usada en el mercado laboral y nos dará un ejemplo práctico de cómo usar los conocimientos adquiridos en nuestra carrera. Para simular dicha rentabilidad es necesario partir de ciertas hipótesis como por ejemplo el número de asegurados que tendrá, tasas de inversión, gastos de administración y operación. En base a esto la Aseguradora pronosticará las ganancias en dinero que tendría por la venta de algún seguro en específico. FACTORES DE CANCELACIÓN: Estos son factores de ajustes y como su nombre lo dice, corresponden a la frecuencia con la cual los asegurados "cancelan" el seguro, este factor lo calcula la CIA aseguradora en base a su experiencia i.e. analiza el número de asegurados que cancelan su seguro al pasar la vigencia de la póliza, en base a eso se calculan los factores de cancelación. Por ejemplo, supongamos que el factor de cancelación en el año 3 de la vigencia de la póliza es del 0.38, podemos decir entonces que en el tercer año el 38% de los asegurados cancelan su póliza. FACTOR DE RESCATE: Análogamente como la CIA aseguradora calcula los factores de cancelación en base a su experiencia, los factores de rescate se calculan tomando en cuenta el numero de asegurados que hacen uso de los valores de rescate (Seguro Saldado, Seguro Prorrogado, etc), i.e. analiza cuantos asegurados usan el valor de rescate y en base a eso calcula el factor de rescate.
TASAS DEL FONDO DE INVERSIÓN. )(ti No es más que la tasa a la que la CIA aseguradora cree invertirá todo el dinero que le entra ya sea de reserva ó de prima. Que generalmente son mayores al interés técnico. SEGURO A PRIMA UNICA. Consiste en calcular un seguro a prima única dependiendo del tipo del seguro que se va a vender, por ejemplo si queremos calcular un seguro temporal a "n" años a prima única, con una Suma Asegurada (SA) se calcularía de la siguiente manera:
SADMM
PUAx
nxxnx *:
+−==

6
ANUALIDAD ANTICIPADA. No es mas que calcular la anualidad anticipada de un seguro, como ejemplo si tenemos un seguro temporal a "n" años con una Suma Asegurada (SA) se calcularía de la siguiente manera:
x
nxxnx D
NNä +−
=:
PRIMA NETA NIVELADA. Es la prima que siempre pagara el asegurado en todas sus anualidades, por ejemplo para un seguro temporal a "n" años.
SANNMM
äPUPNP
nxx
nxx
nxnx *
::
+
+
−
−===
PRIMA DE TARIFA. Esta es la prima que sale al mercado, o prima comercial, en esta prima ya se recargan gastos de gestión externa (GGE) y los gastos de gestión interna (GGI). Se calcula de la siguiente manera:
)1( ggiggePNPTarifa−−
=
TABLA SELECTA (Qt). Esta tabla se calcula a partir de la proporción que existe entre las tasas de mortalidad de la aseguradora y las tasas de la tabla de mortalidad utilizada, es decir, son probabilidades de muerte ajustadas por la Aseguradora en base a su propia experiencia. Generalmente las tasas de mortalidad de la tabla selecta son más grandes que las de una tabla de mortalidad. CALCULO DE LAS FUNCIONES DEL ASSET SHARE: #Aseg: en esta función se calculan los números estimados de asegurados tendrá la aseguradora, para calcular esta columna se osan los factores de cancelación para estimar cuantos asegurados al paso del tiempo van ir cancelando su seguro, se calcula de la siguiente manera:
)1(*## 111 −−− −−= tttt CanQAsegAseg
PRIMA. En esta colma se calcula, cuanto dinero le entra a la aseguradora en primas i.e.
Prima )(#*)( tt AsegPtarifa= G.G.E. Estos Son los gastos de gestión externa, en esta columna la aseguradora calcula cuanto dinero desembolsará por gastos como pago de Agentes de Seguros,
=tGGE Prima GGEt* G.G.I. Estos Son los gastos de gestión interna, en esta columna la aseguradora calcula cuanto dinero desembolsará por Gastos de Administración (Ej. Pago de Nomina de empleados):
=tGGI Prima GGIt* MORTALIDAD. En esta columna se calcula el dinero el cual espera pagar la aseguradora en sumas aseguradas, para ello se tiene que calcular el número esperado de muertos que tendrá.
)0,*#(_ ttt QAsegRoundesperadosMuertos =
En general este producto no da un número entero, de tal forma que se tiene que redondear al entero más próximo. Entonces el dinero que espera pagar la Aseguradora esta dado de la siguiente manera:
SAQAsegMortalidad ttt *)*(#=
RESERVA T. En esta columna se calcula la reserva terminal por asegurado, consiste en calcular la reserva al tiempo "t" por asegurado, para este efecto se usara el método prospectivo. i.e. La reserva terminal por asegurado de un seguro temporal a "n" años al año "t" ó en el año "t" es:
[ ]tx
nxtxnxnxtxt DNNPMMSAnxV
+++++ −−−=
1*)()(*: :
'
La reserva terminal por asegurado de un seguro ordinario de vida (vida entera) al año "t" ó en el año "t" es:

7
[ ]tx
txxtxt DNPMSAxV
+++ −=
1***
La reserva terminal por asegurado de un seguro dotal al año "t" ó en el año "t" es:
[ ]tx
nxtxnxnxnxtxt DNNPDMMSAnxV
++++++ −−+−=
1*)()(*: :
VALOR DE RESCATE. En esta columna se calcula el dinero esperado que piensa pagar la aseguradora por el concepto de Valor de Rescate, dicho en otras palabras, la Aseguradora hace un estimado de cuanto dinero piensa desembolsar por que un asegurado decida cancelar su póliza, la forma de calcular es la siguiente; suponiendo que le devolverá el 95% de su reserva matemática una ves aplicándole el factor de rescate que le corresponde:
95.0****#_Re__ ttttt RcteRvaCanAsegEsperadoscatedeValor = RESERVA TERMINAL. En esta columna la aseguradora calcula cuanto dinero tendrá en reserva por todos sus asegurados. i.e.
ttt RvaAsegalTerserva *#min_Re = DIVIDENDOS. Una ves que la aseguradora crea reservas ese dinero lo invierte a una tasa i(t) mayor a la del Interés Técnico, formando así los llamados "dividendos", la forma de calcularlos es:
)90.0*(**# )(1 itiRvaAsegDividendos tttt −= − Suponiendo que dará el 90% de dividendos. FONDO. Esta es una de las funciones más importantes de un Asset Share pues hace uso de la mayoría de las columnas del Asset Share ya que a todas las entradas de dinero a la aseguradora le resta todas las salidas obteniendo así las ganancias. Se calcula de la siguiente manera: Nótese que los GGI y Mortalidad fueron llevados a valor futuro o invertidos medio periodo eso suponiendo que el dinero que gasto la compañía en nomina de empleados y muertes
ocurridas fueron entregados a mitad de año. VP PRIMAS. En esta columna se llevan a valor presente el dinero en primas que le entraron a la aseguradora, se calcula de la siguiente manera:
)1(1
)1(2
)1(1 )1(*.....*)1(*)1(*PrPr −
−−− +++= ttt iiiimaimasVP
CONSTRUCCIÓN DE LA TABLA DE VALORES GARANTIZADOS PARA EL ASEGURADO
Las siguientes columnas si bien no forman parte del Asset Share si son muy importantes verlas de manera didáctica y se calculan para mostrar un especie de catalogo al asegurado, en donde se le explique qué puede hacer con su dinero en reserva si decide cancelar su seguro. VALOR DE RESCATE. Forma parte de los "valores garantizados", cuando el asegurado decide no continuar con el seguro entonces la Aseguradora le devuelve "parte" de la Reserva Matemática, cabe aclarar que este como todos los valores garantizados solo se tomaran en cuenta cuando el asegurado ya haya permanecido al menos dos años con la aseguradora. Se calcula de la siguiente manera:
95.0**__ ttt RcteRvaAsegporValRcte = El 0.95 corresponde al porcentaje que la aseguradora dará de la reserva que a creado el asegurado una ves aplicado el factor de rescate que le corresponde. SEGURO SALDADO Si el asegurado decide no seguir pagando la prima y desea continuar protegido, el valor de rescate puede ser utilizados para pagar el plazo que falte de transcurrir de la vigencia del Contrato.
De esta forma, el asegurado utiliza el Valor de Rescate para pagar una cobertura a prima única, por le mismo plazo que contrató originalmente, pero con menor suma asegurada. Supongamos un Seguro Temporal n años, entonces la formula se deduce de la siguiente manera:
ttttt
ttttt
DivdendosVRscateiMortalidadGGIiGGEimaFondoFondo
−−++−
+−+= −
])1(*)[(
)]1(*)Pr[(2/1
1

8
AseguradaSumaNueva
t
SegurodelCosto
tntxAseguradodelserva
t SaldadoSeguroAAsegporValRcte ___:
Re
⋅=−+
ttx
nxtxt SaldadoSeguro
DMM
AsegporValRcte _)(
__+
++ −=
tx
nxtx
tt
DMM
AsegporValRcteSaldadoSeguro
+
++ −=
)(__
_
(Tarea 5, Construir la formula para calcular el Seguro Saldado en el tiempo t para un seguro Ordinario de Vida) SEGURO PRORROGADO
Si el asegurado decide no seguir pagando la prima y desea continuar protegido con la misma Suma Asegurada, el valor de rescate podrá ser utilizado para este fin.
De esta forma, el asegurado utiliza el Valor de Rescate para pagar una cobertura a prima única, por la misma suma asegurada que contrató originalmente, pero por un plazo menor (plazo prorrogado). La deducción de la formula es la siguiente:
⎟⎠
⎞⎜⎝
⎛⋅=
+ 365_
__1:
Re
t
añounenSegurodelCostotx
Aseguradodelserva
tprorrogadoSeguro
AAsegporValRcte
Entonces:
1
_ __ *365*
tt
x t x t
x t
ValRcte por AsegSeguro prorrogado M M SAD
+ + +
+
⎛ ⎞⎜ ⎟⎜ ⎟=
−⎜ ⎟⎜ ⎟⎝ ⎠
CUADRO DE RENTABILIDAD. Finalmente es hora de saber que rentabilidad (que tan rentable fue el seguro que vendió la aseguradora) tubo la aseguradora con el seguro que vendió. Para ello necesitamos calcular el Valor Presente del Fondo VPF (cuanto dinero obtuvo al invertir la aseguradora) y el valor presente de las primas VPP (cuanto dinero en primas entro a la aseguradora traído a valor presente.)
∑=
=n
ttimasVPVPP
1Pr
1
)(1
)2(1
)1( )1(*......*)1(*)1(* −−−+ +++= tnt iiiFondoVPF
PORCENTAJE DE UTILIDAD.
VPPVPFutilidaddePorcentaje =__ %
(Tarea 6, Calcular un Asset Share se anexara Asset en Excel para un temporal 10 años) (Tarea 7, Calcular un Asset Share se anexara Asset en Excel para un temporal 20 años) (Tarea 8, Calcular un Asset Share se anexara Asset en Excel para un Ordinario de Vida) 3.- PROBABILIDAD DE VIDA CONJUNTA Y DE ÚLTIMO SOBREVIVIENTE Recordemos la probabilidad de dos o más independientes que se presentan juntos o en sucesión es el producto de sus probabilidades marginales:
)()()( BPAPByAP ⋅=
Así pues, ¿Cuál es la probabilidad de que dos personas, una de edad “x” y otra de edad “y” ambas lleguen con vida al siguiente año?, si suponemos que se trata de dos eventos independientes, es decir, que la muerte de una persona en nada afectará a la otra, tendríamos que:
yxyx ppp ⋅=:
Ó dicho de otra manera:
yx
yx
y
y
x
xyx l
lll
llp
:
1:111:
++++ =⋅=
Es decir, por notación:

9
• 111:1 ++++ ⋅= yxyx lll
• yxyx lll ⋅=: Pongamos un ejemplo de lo antes descrito: ¿Cuál es la probabilidad de que 2 personas una de edad 18 y otra de edad 20 ambas lleguen con vida al siguiente año?
20:18
20:19
20
21
18
1920:18 l
lll
ll
p =⋅=
Probabilidad de vida conjunta de m participantes: Se conoce así por que el grupo se destruye si alguno de los integrantes fallece, ó dicho de otra manera todos los participantes deben de continuar con vida.
En general supongamos que las vidas para edades ix para i=1,2,...,m son independientes, entonces la probabilidad de que un grupo vida conjunta de “m” vidas todas sobrevivan n años más:
m
m
mxxx
nxnxnxxxxn l
lp
:...::
:...:::...::
21
21
21
+++=
Ejemplo: ¿Cuál es la probabilidad de que un grupo de 3 personas de edades 18, 19 y 20 todas lleguen con vida dentro de 3 años:
20:19:18
320:319:31820:19:183 l
lp +++=
Probabilidad de destrucción de un grupo de m participantes Ya vimos la probabilidad de que de un grupo de m participantes todos sobrevivan, pero cuál es la probabilidad de que de un grupo de m participantes todos mueran (destrucción del grupo). Para encontrar dicha probabilidad partamos de lo siguiente: ¿Cuál sería la probabilidad de que en un grupo de 2 personas, una de edad “x” y otra de edad “y” ninguna llegue con vida al siguiente año:
yxyxyxyxyx pppppqqq :: 1)1()1( +−−=−⋅−=⋅=
Ahora bien, supongamos que las vidas para edades ix con i=1,2,...,m son independientes, entonces la probabilidad de que un grupo vida conjunta de “m” vidas muera a la edad
nxi + se puede expresar por:
m
m
mmxxx
xxxnxnxnxnxxxn l
dqqqq
:...::
:...:::...::
21
21
2121)()()( =⋅⋅⋅= …
Ejemplo: ¿Cuál es la probabilidad de que de un grupo de 3 personas con edades 18, 20 y 22 todas mueran dentro de 3 años?
22:20:18
22:20:18322320318322:20:183 )()()(
ldqqqq =⋅⋅=
Otra pregunta interesante podría ser:
¿Cuál es la probabilidad de que de un grupo de m participantes de edades ix todos mueran entre los años n y r con n < r?
m
m
mmxxx
nxnxnxnrxnrnxnrnxnrnxxxnrn l
dqqqq
:...::
:...:::...::
21
21
2121)|()|()|(| +++−
−−−− =⋅⋅⋅= …
Ejemplo: ¿Cuál es la probabilidad de que de un grupo de 3 personas de edades 18, 20, y 22 todas mueran entre los años 6 y 8?
22:20:18
28:26:242
22:20:18
622:620:618222262026182622:20:1826
22686206861868622:20:18686
)|()|()|(|
)|()|()|(|
ld
ld
qqqq
qqqq
==⋅⋅=
⋅⋅=
+++
−−−−
Como hemos visto hasta ahora hemos calculado probabilidad de sobrevivencia y destrucción de un grupo de m participantes los cuales todos en su conjunto deben sobrevivir o desaparecer. Ahora veremos el caso donde no a todos les tenga que ocurrir la contingencia: Probabilidad de vida conjunta de último sobreviviente. Si se recuerda en el capitulo anterior, vida conjunta de m participantes, este era destruido cuando cualquier participante falleciera, es decir todos los participantes debían continuar con vida. Por lo tanto el grupo de último sobreviviente, se destruye a la muerte del último sobreviviente.

10
¿Cuál es la probabilidad de que en un grupo de 2 personas de edades 1x y 2x al menos una llegue con vida el siguiente año?
∑=
+−+=
−+=
−−−=
−=
−=
2
1:
12
:
.
:
1
:
21
2121
21
21
2121
)1(
)1)(1(1
))((1
1
ixxx
xxxx
xx
xx
mueranambosquedeprob
xxxx
pp
ppp
pp
qp
i
Ahora, ¿Cuál es la probabilidad de que en un grupo de 3 personas de edades 1x , 2x y 3x al menos una llegue con vida el siguiente año?
∑ ∑=
+
<=
−+−=
+−−−++=
−−−−=−=−=
3
1::
133
1:
:::::
::
1
::
321
321323121321
321321321321
)1(
)1)(1)(1(1))()((11
ixxx
jii
xxx
xxxxxxxxxxxx
xxxxxxxxxxxx
ppp
ppppppp
pppqqqqp
jii
Ahora, ¿Cuál es la probabilidad de que en un grupo de 4 personas de edades 1x , 2x , 3x y
4x al menos una llegue con vida el siguiente año?
∑ ∑∑=
+
<<=
<=
−++−=
−++++
−−−−−−
+++=
−−−−−=
−=−=
4
1:::
144
1::
4
1:
:::::::::::
::::::
:::
1
:::
4321
4321432431421321
434232413121
4321
4321
432143214321
)1(
)1)(1)(1)(1(1
))()()((11
ixxxx
kjii
xxx
jii
xxx
xxxxxxxxxxxxxxxx
xxxxxxxxxxxx
xxxx
xxxx
xxxxxxxxxxxx
pppp
ppppp
pppppp
pppp
pppp
qqqqqp
kjijii
Finalmente, Cuál es la probabilidad de que en un grupo de m personas de edades 1x , 2x ,
3x ,…, mx al menos una llegue con vida el siguiente año?
∑ ∑∑=
+
<<=
<=
−+++−=m
ixxx
mm
kjii
xxx
m
jii
xxxxxx mkjijiimppppp
1:::
1
1::
1:
1
::: 2121)1( …… …
Cuál es la probabilidad de que en un grupo de m personas de edades 1x , 2x , 3x ,…, mx al menos una sobreviva n años más?
∑ ∑∑=
+
<<=
<=
−+++−=m
ixxxn
mm
kjii
xxxn
m
jii
xxnxnxxxn mkjijiimppppp
1:::
1
1::
1:
1
::: 2121)1( …… …
Ejemplo: Cuál es la probabilidad de que en un grupo de 3 personas de edades 18, 20 y 22 al menos una sobreviva 3 años más?
∑ ∑=
+
<=
−+−=3
122:20:183
133
1:33
1
22:20:183 )1(i
jii
xxx ppppjii
22:20:18322:20322:18320:183223203183 ppppppp +−−−++= Ahora nos enfrentamos a otro problema: ¿ Cuál es la probabilidad de que en un grupo de 3 personas de edades 18, 20 y 22 al menos dos sobreviva 3 años más?, o más aún:
¿ Cuál es la probabilidad de que en un grupo de m personas de edades 1x , 2x , 3x ,…,
mx al menos r sobrevivan n años más? Para resolver estas preguntas introduciremos el concepto de:
][
::: 21
r
xxxn mp …
Que denota la probabilidad de que en un grupo de m personas con edades 1x , 2x , 3x ,…,
mx exactamente r sobrevivan n años más. Si conociéramos esta probabilidad nuestra pregunta principal:

11
Cuál es la probabilidad de que en un grupo de m personas de edades 1x , 2x , 3x ,…,
mx al menos r sobrevivan n años más sería: ][
:::
]1[
:::
][
:::::: 21212121
m
xxxn
r
xxxn
r
xxxn
r
xxxn mmmmpppp ………… +++=
+
Centrémonos entonces en calcular: ][
::: 21
r
xxxn mp …
¿Cuál es la probabilidad de que en un grupo de 2 personas una edad 1x y otra de edad
2x exactamente una llegue con vida al siguiente año? En este caso recordemos que para dos eventos independientes:
)()()( BPAPBóAP +=
Entonces la probabilidad de que en un grupo de 2 personas una edad 1x y otra de edad
2x una llegue con vida al siguiente año, sería lo mismo que decir que ( 1x ) llegue con vida
al siguiente año y la otra muera ó ( 2x ) llegue con vida al siguiente año y la otra muera:
§ 21121 :)1( xxxxx pppp −=−
§ 21212 :)1( xxxxx pppp −=−
Finalmente la probabilidad que queríamos encontrar seria:
( ) ( )
21
212121221121
:12
2
1
:::
]1[
:
)1(2
2
xxi
x
xxxxxxxxxxxx
pp
pppppppp
i
+
=
−+=
−+=−+−=
∑
¿Cuál es la probabilidad de que en un grupo de 3 personas una edad 1x , otra de edad
2x y otra de edad 3x exactamente una llegue con vida al siguiente año? Usando lo que vimos en el ejemplo anterior tendríamos ahora 3 casos:
• Solo llegue con vida 1x ó
• Solo llegue con vida 2x ó
• Solo llegue con vida 3x Es decir:
• 32131211321 ::::)1)(1( xxxxxxxxxxx ppppppp +−−=−−
• 32132212312 ::::)1)(1( xxxxxxxxxxx ppppppp +−−=−−
• 32132313213 ::::)1)(1( xxxxxxxxxxx ppppppp +−−=−− Sumando:
321
321
223121
221321
::13
3
1:
3
1
::
:::
]1[
::
)1(32
3
222
xxx
jii
xxi
x
xxx
xxxxxx
xxxxxx
ppp
p
ppp
pppp
jii
+
<==
−++=
+
−−−
++=
∑∑
¿Cuál es la probabilidad de que en un grupo de 4 personas una edad con edades 1x ,
2x , 3x y 4x exactamente una llegue con vida al siguiente año? Usando lo que vimos en el ejemplo anterior tendríamos ahora 4 casos:
• Solo llegue con vida 1x ó
• Solo llegue con vida 2x ó
• Solo llegue con vida 3x ó
• Solo llegue con vida 4x Es decir:
4321431421321
41312114321
:::::::::
:::)1)(1)(1(
xxxxxxxxxxxxx
xxxxxxxxxxx
pppp
pppppppp
−+++
−−−=−−−
4321
43241231242322124312
:::
:::::::::)1)(1)(1(
xxxx
xxxxxxxxxxxxxxxxxxxx
p
ppppppppppp
+
+++−−−=−−−
4321
42341321343231334213
:::
:::::::::)1)(1)(1(
xxxx
xxxxxxxxxxxxxxxxxxxx
p
ppppppppppp
+
+++−−−=−−−

12
4321
32431421434241443214
:::
:::::::::)1)(1)(1(
xxxx
xxxxxxxxxxxxxxxxxxxx
p
ppppppppppp
+
+++−−−=−−−
Finalmente la probabilidad que buscamos es:
4321431432421321
43423241312143214321
:::::::::::
::::::
]1[
:::
43333
222222
xxxxxxxxxxxxxxxx
xxxxxxxxxxxxxxxxxxxx
ppppp
ppppppppppp
−++++
−−−−−−+++=
O bien:
43214321 :::14
4
1::
4
1:
4
1
]1[
::: )1(432 xxxx
kjii
xxx
jii
xxi
xxxxx pppppkjijii
+
<<=
<==
−+++= ∑∑∑
De acuerdo a todo lo anterior. ¿Cuál es la probabilidad de que en un grupo de “m” personas de edades
mxxxx ,...,,, 321 , respectivamente exactamente una llegue con vida al siguiente año?
mkjijiim xxxm
m
kjii
xxx
m
jii
xx
m
ixxxx Pmpppp :...::
1
1::
1:
1
]1[
::....:: 2121)1)((....32 +
<<=
<==
−+−+−= ∑∑∑
Pero seguimos sin encontrar ][
::: 21
r
xxxn mp … , por lo que el último resultado evidencia lo
complejo que es encontrar dicha probabilidad. Ahora analicemos otro resultado....
¿Cuál es la probabilidad de que de un grupo de tres personas de edades 321 ,, xxx iguales exactamente dos lleguen con vida? Para resolver la pregunta hay que analizar los casos posibles:
• Que x1 y x2 lleguen con vida y x3 muera ó • Que x1 y x3 lleguen con vida y x2 muera ó • Que x1 y x3 lleguen con vida y x1 muera
Dicho de otra manera:
• 321 xxx qpp ó
• 331 xxx qpp ó
• 132 xxx qpp Y dado que x1=x2=x3=x (pues las edades son iguales) la probabilidad que buscamos es:
( ) ( )
( ) ( ) ( ) ( ) 232232
12]2[
:::
)!23(!2!3
112123
3)(3321
−−
−=
⋅⋅⋅⋅
=
==++=
xxxx
xxxxxxxxxxxxxxxxx
qpqp
qpqppqppqppqppp
Finalmente tenemos que:
( ) ( ) 23232
]2[
::: 321
−= xxxxx qpCp
Ahora bien, ¿qué pasa para un grupo de 4 personas de la misma edad x , exactamente 2 lleguen con vida? Analicemos los casos:
• xxxx qqpp ó
• xxxx qpqp ó
• xxxx pqqp ó
• xxxx qppq ó
• xxxx pqpq ó
• xxxx ppqq Entonces tenemos que:
( ) ( ) ( ) ( ) 24242
242]2[
:::: )!24(!2!46
4321
−− =−
== xxxxxxxxxxxx qpCqpqqppp
Ahora que pasa si de ese mismo grupo de personas queremos que exactamente 3 sobrevivan:
• xxxx qppp ó
• xxxx pqpp ó
• xxxx ppqp ó
• xxxx pppq Finalmente tendríamos que:

13
( ) ( ) ( ) ( ) 34243
343]3[
:::: )!34(!3!44
4321
−− =−
== xxxxxxxxxxxx qpCqpqpppp
Lo que podemos concluir es que la probabilidad de que de un grupo de m personas de la misma edad exactamente r lleguen con vida es:
( ) ( ) rmx
rx
mr
r
xxx qpCpm
−=][
:...:: 21
Este último resultado nos sirve para encontrar la probabilidad de que de un grupo de m personas de la misma edad al menos r lleguen con vida:
][
:...::
]1[
:...::
][
:...:::...:: 21212121...
m
xxx
r
xxx
r
xxx
r
xxx mmmmpppp +++=
+
Este último resultado solo funciona si las edades de los integrantes del grupo son las mismas, pero qué pasa si no lo son? Método Z Para resolver este problema vamos utilizar un Método conocido como “Z” para aproximar dicha probabilidad para ello vamos a definir:
mrmtrtrrr
r
xxx ZkZkZkZkZpm −+++ ++++++= ……2211
][
:...:: 21…(1)
Donde:
• sZ : simboliza la suma de las combinaciones de probabilidades de supervivencia al final del año de m participantes tomados de s maneras
• sk : simboliza una constante de ponderación Encontremos los Valores de Z y de K. Para ello recordemos uno de los resultados que obtuvimos:
( ) ( ) rmx
rx
mr
r
xxx qpCp −=][
:...::
Y por otro lado recordemos el teorema del binomio:
( ) ∑=
−=+n
k
kknnk
n yxCyx0
O bien:
( ) ∑=
−−=−n
k
kknnk
kn yxCyx0
)1(
Entonces:
( ) ( )
( ) ( )
( )
rmx
rmrm
rmrx
mr
xrmr
xmrx
rmrx
mrx
rmrx
mr
rm
k
kx
rmk
krx
mr
rm
k
kx
krmrmk
krx
mr
rmx
rx
mr
rmx
rx
mr
r
xxx
pCpCpCpCpCpCpCpC
pCpC
pCpC
ppC
qpCp
−−−
−
−−−
−
=
−
−
=
−−−
−
−
−++
−+−+−=
−=
−=
−=
=
∑
∑
)1(
)1()1()1(
)1(
1)1(
1
22
211
100
00
0
][
:...::
…
O bien: mx
mr
rmrx
rmmr
rx
rmmr
rx
mr
r
xxx pCpCCpCCpCp −+−+− −+++−= )1(22
11
][
:...:: … …(2)
Por otro lado dado que Zs Simboliza la suma de las combinaciones de probabilidades de supervivencia de m participantes tomados de s maneras. Entonces podemos suponer que:
sx
ms
m
s
Pss pCCZ sxxx ==∑
=1
:...:2:1
Si sustituimos esto en (1):
1222
111
][
:...:: 21
−−
++
++
++ ++++++= m
xrmtr
xmtrt
rx
mr
rx
mr
rx
mr
r
xxx pkpCkpCkpCkpCpm
……
Llamemos este ultimo resultado Ecuación (3) Para encontrar los valores K igualamos miembro a miembro la Ecuación 2 y 3, es decir, qué valor debe tomar K para que la ecuación 3 sea igual a la ecuación 2? El primero miembro es exactamente igual:
rx
mr
rx
mr pCpC =
El segundo miembro: 1
111
1+
++− =− r
xmr
rx
rmmr pCkpCC
Entonces:
11
1
11
1
11
1+
+
−
++
+−
−=−
=−
= rmr
rmmr
rx
mr
rx
rmmr C
CCC
pCpCCk
22
2
22
2
22
2+
+
−
++
+−
=−
=−
= rmr
rmmr
rx
mr
rx
rmmr C
CCC
pCpCCk

14
O bien:
srsm
sr
rms
mr
srx
msr
srx
rms
mr
s CCCC
pCpCCk +
+
−
++
+−
=−
=−
=
Si sustituimos los valores K que acabamos de encontrar en la ecuación 1 hasta m-r tenemos que:
122
211
1
][
:...:: )1()1(21 −−
−+
++
++
+ −++−+++−= mmrm
rmtr
trt
tr
rr
rr
r
xxx ZCZCZCZCZpm
……
trtr
t
rm
t
tr
xxx ZCpm +
+−
=∑ −=0
][
:...:: )1(21
Con esto podemos encontrar la probabilidad de que en un grupo de m participantes con
edades ix con i=1,2,..,m diferentes exactamente r lleguen con vida. Ejemplo: ¿Cuál es la probabilidad de que en un grupo de 4 personas con edades
321 ,, xxx y 4x exactamente 2 lleguen con vida el siguiente año?
( )4321
432431421321
434232413121
4321
:::
::::::::
::::::
432
2222
21212
1202
022
24
0
]2[
:::
6
3
63
)1(
xxxx
xxxxxxxxxxxx
xxxxxxxxxxxx
tt
tt
txxxx
p
pppp
ppppppZZZ
ZCZCZCZCp
+
+++−
+++++=
+−=
+−=−= ++
+++
++
−
=∑
Ejemplo: ¿Cuál es la probabilidad de que en un grupo de 4 personas con edades
321 ,, xxx y 4x exactamente 2 sobrevivan 5 años más?
( )4321
432431421321
434232413121
4321
:::5
::5::5::5::5
:5:5:5:5:5:5
432
2222
21212
1202
022
24
0
]2[
:::5
6
3
63
)1(
xxxx
xxxxxxxxxxxx
xxxxxxxxxxxx
tt
tt
txxxx
p
pppp
ppppppZZZ
ZCZCZCZCp
+
+++−
+++++=
+−=
+−=−= ++
+++
++
−
=∑
En ese sentido podemos suponer que
trtr
t
rm
t
tr
xxxn ZCpm +
+−
=∑ −=0
][
:...:: )1(21
Ya hemos resuelto casi todas nuestras preguntas, y solo nos falta una:
∑∑∑=
−
=+
+
=
−==m
rs
rm
tts
tst
tm
rs
s
xxxn
r
xxxn ZCppmm
0
][
:...:::...:: )1(2121
Pero resolver esta suma aún suena complicado por lo que veremos si hay manera de reducirla, para ello intentemos calcular la siguiente probabilidad:
]4[
:::
]3[
:::
]2[
:::
4
2
][
:::
2
::: 43214321432143214321 xxxxxxxxxxxxs
s
xxxxxxxx ppppp ++==∑=
Calculemos por separado cada una de las probabilidades:
444
44
0
]4[
:::
44133
334
0
]3[
:::
4423
3122
224
0
]2[
:::
)1(
)1(
)1(
4321
4321
4321
ZZCp
ZCZZCp
ZCZCZZCp
tt
tt
txxxx
tt
tt
txxxx
tt
tt
txxxx
=−=
−=−=
+−=−=
++
−
=
++
−
=
++
−
=
∑
∑
∑
Finalmente:

15
( ) ( ) ( )
( ) ( )
( ) ( ) ( )
( )∑=
−−
−
−−
−−−
−−−
−
−=
−+−+−=
+−=
+−=+−=
+−+−−=
+−++−=
+−++−=
++=
4
2
12
2
41424
243
1323
232
1212
224
323
212
10
4323
212
324
2132
40
41
424
30
3132
44414
4233
312
444134
423
312
]4[
:::
]3[
:::
]2[
:::
2
:::
1
111
4321432143214321
ss
ss
s
xxxxxxxxxxxxxxxx
ZC
ZCZCZC
ZCZCZCZCZCZCZCZZ
CCCZCCZZZZCZCZZCZZZCZZCZCZ
pppp
Generalizando este resultado encontramos la probabilidad tan añorada:
∑=
−−
−−=m
rss
srs
rsr
xxx ZCpm
1:...:: )1(
21
Como en el valor Z va implícito el número de años de supervivencia:
∑=
−−
−−=m
rss
srs
rsr
xxxn ZCpm
1:...:: )1(
21
Ejemplo: Cuál es la probabilidad de que en un grupo de 4 personas de edades 321 ,, xxx y
4x al menos 2 sobrevivan n años más?
( )4321
432431421321
434232413121
4321
:::
::::::::
::::::
432
4323
2124
14243
13232
4
2
12
22
:::
3
2
32
)1(
xxxxn
xxxnxxxnxxxnxxxn
xxnxxnxxnxxnxxnxxn
ss
ss
sxxxxn
p
pppp
ppppppZZZ
ZCZCZZCZCZZCp
+
+++−
+++++=
+−=
+−=+−=−= −−
−−
=
−−
−∑
Como podemos ver el método “Z” nos ayuda a encontrar este tipo de probabilidades de manera rápida.
Anualidades para más de 2 personas 4.- Anualidades Vitalicias Recordemos que en el caso de 1 persona una anualidad vitalicia vencida a edad x se calculaba de la siguiente manera:
x
x
x
wxx
xx
ww
xx
xx
x
wxw
xxx
x
x
wxw
xx
x
wxw
x
x
x
x
xxwxw
xx
x
txt
tx
DN
DDDD
lVlVlVlV
llVlVlV
VV
llVlVlV
ll
Vll
Vll
V
pVpVpVpVa
121
22
11
22
11
22
11
2211
221
1
...
...
...
+++
++
++−
++
−++−++
−−
−
=
=+++
=
+++=
+++=
+++=+++=
+++==∑
……
…
ω
En el caso de dos personas, el valor presente de 1 u.m. de personas de edades x1 y x2 , mientras las dos estén con vida sería:
∑∞
=
=1
:: 2121t
xxtt
xx pVa
Definimos lo siguiente:
• xxxx lDD =
• xxxxxx llDD =
• ∑=
++=ϖ
0:
ttxtxxx DN
• yxxy lDD =
Entonces:

16
( )
21
21
21
21
21
2121
21
1
2121
1
21
:
1:11
2211
:
2:22
1:11
:
......
xx
xx
xx
ttxtx
xx
xxxx
xxx
xxxxx
xx
DN
lD
lD
lDlDlD
lVlVlVV
a
++
∞
=++
++++++++
==
++=
++=
∑
En el caso de tres personas:
321
321
321321::
1:1:1
1::::
xxx
xxx
txxxt
txxx D
NpVa +++
=∑ ==ω
En el caso de m personas:
m
m
mmxxx
xxx
txxxt
txxx D
NpVa
:..::
1:...:1:1
1:..:::..::
21
21
2121
+++
=∑ ==ω
Para el caso anticipado:
m
m
mmxxx
xxx
txxxt
txxx D
NpVä
:..::
:...::
0:..:::..::
21
21
2121===∑
=
ω
Anualidades Temporales n años: Recordemos que para el caso de una persona, la anualidad vencida temporal n años se calcula:
x
nxxn
txt
tnx D
NNpVa 11
1:
+++
=
−==∑
Dado los resultados anteriores una anualidad vencida temporal n años para dos personas sería:
21
2121
2121:
1:11:1
1:::
xx
nxnxxxn
txxt
tnxx D
NNpVa ++++++
=
−==∑
Para el caso de m personas:
m
mm
mmxxx
nxnxnxxxxn
txxxt
tnxxx D
NNpVa
:..::
1:...:1:11:...:1:1
1:..::::..::
21
2121
2121
+++++++++
=
−==∑
Para el caso anticipado:
m
mm
mmxxx
nxnxnxxxxn
txxxt
tnxxx D
NNpVä
:..::
:...:::...::1
0:..::::..::
21
2121
2121
+++−
=
−==∑
Recordemos que hasta ahora solo hemos trabajado con edades iguales, trabajemos con otros casos: Por ejemplo cual es la anualidad vitalicia vencida para un grupo de dos personas de edades diferentes si se desea que exactamente alguna de ellas sobreviva:
( )
∑ ∑∑
∑∑
= ==
==
−+=−+=
=−+==
ϖ ϖϖ
ϖϖ
1:
1:
1
11
]1[
:
]1[
:
21212121
21212121
2
2
txxxx
txxt
txt
t
txt
t
txxxxt
t
txxt
txx
aaapVpVpV
ppppVpVa
Para el caso de tres personas:
( )
321323121321
321323121321
321321
3222
3222
:
1
1
]1[
::
]1[
::
xxxxxxxxxxxx
txxxxxxxxxxxxt
t
txxxt
txxx
aaaaaaa
ppppppppppppV
pVa
+−−−++=
+−−−++=
==
∑
∑
=
=
ϖ
ϖ
Finalmente para m personas:
mkjijiim xxxm
m
kjii
xxx
m
jii
xx
m
ixxxx amaaaa :...::
1
1::
1:
1
]1[
::....:: 2121)1)((....32 +
<<=
<==
−+−+−= ∑∑∑
Para el caso de que exactamente r personas lleguen vida:
][
:...::1
][
:...:: 2121
r
xxxtt
tr
xxx mmpVa ∑
∞
=
=
Ahora bien, cuál es la anualidad vitalicia vencida para un grupo de m personas de edades diferentes si se desea que exactamente al menos r sobrevivan sobreviva:
][
:...::
]1[
:...::
][
:...:::...:: 21212121...
m
xxx
r
xxx
r
xxx
r
xxx mmmmaaaa +++=
+

17
O dicho de otra manera:
r
xxxtt
tr
xxx mmpVa :...::
1:...:: 2121 ∑
∞
=
=
Se recomienda usar el Método Z
∑=
−−
−−=m
rs
as
srs
rsr
xxxs
mZCa 1
:...:: )1(21
Ejemplo: Calcula el valor presente de 1 u.m. de un anualidad vitalicia siempre que al menos 2 de 4 integrantes de un grupo de edades x1, x2, x3, y x4 estén vivos:
( )4321
432431421321
434232413121
432
432432
4321
:::
::::::::
::::::
432
4323
2124
14243
13232
4
2
12
22
:::
3
2
32
)1(
xxxx
xxxxxxxxxxxx
xxxxxxxxxxxx
aaa
aaaaaa
s
as
ss
sxxxx
a
aaaa
aaaaaaZZZ
ZCZCZZCZCZZCa s
+
+++−
+++++=
+−=
+−=+−=−= −−
−−
=
−−
−∑
5. Primas Netas Únicas (Costo del Seguro) Recordemos que para el caso de una sola persona, la prima neta única para un seguro ordinario de vida es:
x
x
x
ttx
txt
tx D
MD
CqVA ===
∑∑ =
+
=−
ω
ω0
01
Definamos:
• yxyx dCC =:
• ∑=
++=ω
0:
ttytxyx dCM
Entonces la prima neta única de un seguro ordinario de vida para dos personas sería:
21
2121
2121:
:0
0:1:
xx
xx
x
ttxtx
txxt
txx D
MD
dCqVA ===
∑∑ =
++
=−
ω
ω
Para 3 personas:
321
321
321
321
321321::
::
::
0:
0::1::
xxx
xxx
xxx
ttxtxtx
txxxt
txxx D
MD
dCqVA ===
∑∑ =
+++
=−
ω
ω
Para m personas:
m
m
m
m
mmxxx
xxx
xxx
ttxtxtx
txxxt
txxx D
MD
dCqVA
:...::
:...::
:...::
0:...:
0:...::1:...::
21
21
21
21
2121===
∑∑ =
+++
=−
ω
ω
En el caso de un seguro temporal n años recordemos que para una sola persona:
x
nxxn
txt
tnx D
MMqVA +
=−
−==∑
11:
En el caso de dos personas:
21
2121
2121:
::
0:1::
xx
nxnxxxn
txxt
tnxx D
MMqVA ++
=−
−==∑
Para m personas:
m
mm
mmxxx
nxnxnxxxxn
txxxt
tnxxx D
MMqVA
:..::
:..:::..::
1:..::1::..::
21
2121
2121
+++
=−
−==∑

18
Ejemplos: Cual sería el costo de un seguro con una suma asegurada de 1 u.m. si dicha suma se entrega si y solo si exactamente 2 participantes de 4 de edades x1, x2, x3 y x4 mueren antes de n años (utilizando el método Z).
( )nxxxx
nxxxnxxxnxxxnxxx
nxxnxxnxxnxxnxxnxx
AAA
AAAAt
tt
t
t
n
txxxxn
t
tnxxxx
A
AAAA
AAAAAAZZZ
ZCZCZCZC
qVA
t
::::
::::::::::::
::::::::::::
432
422
2312
1202
022
24
0
1
]2[
:::1
]2[
::::
4321
432431421321
434232413121
432
4322
43214321
6
3
63
)1(
+
+++−
+++++=
+−=
+−=−=
=
++++
+−
=
= −
+∑
∑
Si se quiere que al menos 2 lleguen con vida:
( )nxxxx
nxxxnxxxnxxxnxxx
nxxnxxnxxnxxnxxnxx
AAA
AAAAAA
s
As
ss
s
n
txxxxn
t
tnxxxx
A
AAAA
AAAAAAZZZ
ZCZCZZCZCZZC
qVA
s
::::
::::::::::::
::::::::::::
432
4323
2124
14243
13232
4
2
12
2
1
2
:::1
2
::::
4321
432431421321
434232413121
432
432432
43214321
3
2
32
)1(
+
+++−
+++++=
+−=
+−=+−=−=
=
−−
−−
=
−−
−
= −
∑
∑
PRIMAS NETAS NIVELADAS ANUALES Prima Nivelada para un seguro ordinario de vida Recordemos que para una persona:
x
xx ä
AP =
En el caso de dos personas caso vida conjunta:
21
21
21
21
21
21
21:
:
1:
1:1
:
::
xx
xx
txxt
t
txxt
t
xx
xxxx N
M
pV
qV
äA
P ===
∑
∑
=
=−
ω
ω
Para m personas:
m
m
m
m
m
m
mxxx
xxx
txxxt
t
txxxt
t
xxx
xxxxxx N
M
pV
qV
äA
P:..::
:..::
1:..::
1:..::1
:..::
:..:::..::
21
21
21
21
21
21
21===
∑
∑
=
=−
ω
ω
En el caso donde exactamente r llegan con vida:
][
:...::
][
:...::][
:...::
21
21
21 r
xxx
r
xxxr
xxx
m
m
m
ä
AP =
En el caso donde al menos r llegan con vida:
r
xxx
r
xxxr
xxx
m
m
m
ä
AP
:...::
:...:::...::
21
21
21=
Prima Nivelada para un Seguro Temporal n años
Recordemos que para una persona:
nx
nxnx ä
AP
:
:: =
Para el caso de dos personas:

19
nxnxxx
nxnxxxn
txxt
t
n
txxt
t
nxx
nxxnxx NN
MM
pV
qV
ä
AP
++
++
=
=−
−
−===
∑
∑
2121
2121
21
21
21
21
21::
::
1:
1:1
::
::::
Para m personas:
nxnxnxxxx
nxnxnxxxxn
txxxt
t
n
txxxt
t
nxxx
nxxxnxxx
mm
mm
m
m
m
m
m NNMM
pV
qV
ä
AP
+++
+++
=
=−
−
−===
∑
∑
:..:::..::
:..:::..::
1:..::
1:..::1
::..::
::..::::..::
2121
2121
21
21
21
21
21
En el caso donde exactamente r llegan con vida:
][
::...::
][
::...::][
::...::
21
21
21 r
nxxx
r
nxxxr
nxxx
m
m
m
ä
AP =
En el caso donde al menos r llegan con vida:
r
nxxx
r
nxxxr
nxxx
m
m
m
ä
AP
::...::
::...::::...::
21
21
21=
Para ejemplificar todo lo antes visto, resolvamos el siguiente ejercicio: Calcular la Prima Nivelada de un seguro temporal 3 años para el grupo de vida conjunta de dos personas de edades 37 y 38 años respectivamente que desean recibir una Suma Asegurada de $150,000 considerando una tasa de interés técnico del 4%. Solución:
40:392
39:381
38:370
40:393
39:382
38:371
3
138:37
3
138:371
3:38:37
3:38:373:38:37
)04.1()04.1()04.1()04.1()04.1()04.1(lllddd
pV
qV
äA
P
ttt
ttt
−−
−−−
=
=−
+
+=
===
∑
∑
Considerando que:
nyxxyxy lld ++−= :1 , Entonces tendríamos que:
( ) ( ) ( )40:39
239:38
138:37
041:4040:39
340:3939:38
239:3838:37
140:39
239:38
138:37
040:39
339:38
238:37
1
3:38:37
)04.1()04.1()04.1()04.1()04.1()04.1(
)04.1()04.1()04.1()04.1()04.1()04.1(
lllllllll
llldddP
−−
−−−
−−
−−−
+
−−+−=
=+
+=
Como se ve, la Parte II del curso de Matemáticas Actuariales en general, es lo mismo que la parte I pero extrapolado a 2 o más personas, dado lo complejo que puede llegar a ser se recomienda usar el método de aproximación Z para encontrar resultados más rápidos. A continuación veremos el tema de Tabla de Decrementos múltiples para ello hay que dominar un tópico muy importante: 6. Gompertz-Makeham. Recordemos que en el repaso anterior, se vio a la tabla de mortalidad, que como recordaremos era un cuadro estadístico que resume el impacto de la mortalidad en un grupo cerrado de personas a través del tiempo, dicho estudio lo hacia en el mejor de los casos de
manera anual, es decir, nosotros conocíamos a la serie xl de manera discreta, pues el valor “x” solo podía tomar valores enteros (x=1,2,3,4,5.....), la cuestión aquí es saber por ejemplo, cuantos vivos tengo yo a la edad x= 12.00045, ó a la edad x=19.234676, la tabla de mortalidad no nos lo puede decir, pues sus observaciones son discretas y no continuas. Gompertz intento resolver este tipo de preguntas y lo que hizo simplemente fue asociarle una
función (un modelo matemático) continua a la función discreta xl de la tabla de mortalidad, dicha función tenía que cumplir con emular de la manera más exacta a la función discreta.

20
Es así que se presenta su desarrollo. Recordemos una serie muy particular de la tabla de mortalidad: “Tasa Central de Mortalidad”:
xn
xnxn L
dm =
Es decir, el número de muertos en determinado tiempo, respecto al total de personas “presentes”, Partiendo de esta igualdad y recordando que:
xhxxh dhlhL2
−⋅=
Si suponemos que h es un número muy pequeño podemos decir entonces que:
xxh lhL ⋅= Por lo que tendríamos:
))(( x
hxx
xh
xhxh lh
llLd
m +−==
Gracias a esto definimos a la Tasa Instantánea de Mortalidad xµ :
hll
lhll
llhll
m xhx
hx
hxx
hxx
hxx
hxhhx−
−=−
=−
== +
→
+
→
+
→→ 0000)( lim1lim1))((
limlimµ
Que por definición de Derivada:
( )dxld
dxld
lx
cadenaladereglapor
x
xx
)ln()(1)( −=⋅−=µ
Como x es variable muda:
( )dyld y
y
)ln()( −=µ
Intentemos despejar a yl de la ultima expresión,
( )
( )
( )
0
ln
000
0)(
00)(
)(
00)(
ln)ln()ln()ln(
)ln(
)ln(
ll
ee
ll
llldy
dylddy
lddy
xll
dy
xx
x
y
x
y
x
y
x
y
yy
xxy
==
⎟⎟⎠
⎞⎜⎜⎝
⎛=−==−
=−
=−
⎟⎟⎠
⎞⎜⎜⎝
⎛∫−
∫
∫∫
µ
µ
µ
µ
Finalmente tenemos que: ∫−
⋅=
xy dy
x ell 0)(
0
µ
A esta última ecuación se le conoce como Ecuación Fundamental de la Ciencia Actuarial Hasta ahora ya hemos encontrado un modelo matemático, una función lx continua, pero solo conocemos el “radix” y desconocemos la forma que puede tener la tasa instantánea de mortalidad. Es así que Gompertz también respondió esta pregunta haciendo el siguiente razonamiento: El dijo: “la resistencia del hombre a la muerte, disminuye a una tasa proporcional a ella misma y decrece con el paso del tiempo”. i.e.
Ø )(yµ la podemos ver como la No resistencia a la muerte a morir de tal manera que si )(yµ es muy grande entonces la NO resistencia del hombre a la muerte es muy grande, esto quiere decir que la SI resistencia del hombre al morir es pequeña.
Entonces:

21
Ø )(1 yµ la podemos ver como la SI Resistencia a la muerte o bien la resistencia del
hombre a morir ya que si )(yµ es muy grande entonces, )(1 yµ , es muy pequeña.
Lo que hizo Gompertz entonces es decir que la resistencia del hombre al morir es )(1 yµ la cual es proporcional a ella misma, y esta decrece al paso del tiempo. I.e. entre más tiempo pase la resistencia del hombre es menor. Sea entonces:
Ø h = constante de proporcional que asegura la hipótesis de Gompertz Ø )(1 yµ = resistencia del hombre a la muerte
Ø ⎟⎟⎠
⎞⎜⎜⎝
⎛
)(1ydy
dµ
= tasa de cambio de la resistencia del hombre a morir
⎟⎟⎠
⎞⎜⎜⎝
⎛=−⇒
)(1
)(1
ydyd
yh
µµ
Nótese que el factor "h" esta multiplicado por un signo negativo, esto se debe a que la resistencia del hombre al morir decrece con el paso del tiempo. De esta última expresión ya podemos despejar a )(yµ , entonces:
⎟⎟⎠
⎞⎜⎜⎝
⎛=−
)(1
)(1
ydyd
yh
µµ
⎟⎟⎠
⎞⎜⎜⎝
⎛⎟⎟⎠
⎞⎜⎜⎝
⎛=
⎟⎟⎠
⎞⎜⎜⎝
⎛
=−⇒)(
1ln
)(1)(
1
ydyd
y
ydyd
hµ
µ
µ
Resolviendo la Ecuación Diferencial tenemos que:
∫∫ ⎟⎟⎠
⎞⎜⎜⎝
⎛⎟⎟⎠
⎞⎜⎜⎝
⎛=−⇒ dy
ydydhd
)(1ln
µ
1)(1ln By
hdy +⎟⎟⎠
⎞⎜⎜⎝
⎛=−⇒ ∫ µ
12 )(1ln By
Byh +⎟⎟⎠
⎞⎜⎜⎝
⎛=+⋅−⇒
µ
21)(1ln BBy
yh −+⎟⎟⎠
⎞⎜⎜⎝
⎛=⋅−⇒
µ
Sea BBB ln21 =−
By
yh ln)(
1ln +⎟⎟⎠
⎞⎜⎜⎝
⎛=⋅−⇒
µ
⎟⎟⎠
⎞⎜⎜⎝
⎛=⋅−⇒
)(ln
yByh
µ
⎟⎟⎠
⎞⎜⎜⎝
⎛==⇒
⎟⎟⎠
⎞⎜⎜⎝
⎛
⋅−
)()(
ln
yBee y
Byh
µµ
Bey yh =⇒ ⋅−)(µ
yheBy ⋅⋅=⇔ )(µ
Sea he = C yCBy ⋅=⇒ )(µ
Donde:
Ø B = Deterioro biológico Ø C = Proporción en la que se están muriendo
Sustituyendo este último resultado en:
∫ ⋅−∫−
==
xy
xdyCBdyy
x elell 000
)(
0
µ
Resolvemos primero la integral:
∫∫ −=⋅−x
yx
y dyCBdyCB00

22
Recordemos que: ( ) y
y
Cdy
CCd=
ln
⎥⎦⎤
⎢⎣⎡−
=⎥⎦
⎤⎢⎣
⎡−=−=⋅−⇒ ∫∫
xyxyx
yx
y CCB
CCBdyCBdyCB
0000 lnln
Sea CB
ln−
= gln
[ ] [ ] gCCCgCgdyCB xxxyx
y ln1lnln 0
00
⋅−=−=⎥⎦⎤
⎢⎣⎡=⋅−⇒ ∫
[ ] [ ]10
lnln1 −=⋅−=⋅−⇒ ∫xCx
xy ggCdyCB
[ ]10
ln −=⋅−⇒ ∫xC
xy gdyCB
[ ]10
ln00
)(
0
100 −∫ ⋅−∫−
⋅=⋅===⇒⎥⎦⎤
⎢⎣⎡ − xxC
xy
x
CgdyCBdyy
x glelelellµ
[ ] [ ] xx
xx CC
CCx g
gl
gglgglgll ⋅=
⎥⎥⎦
⎤
⎢⎢⎣
⎡=⋅=⋅=⇒ −− 0
01
01
0
Sea Kgl=0
xx CC
x gKggll ⋅=⋅=⇒ 0
xCx gKl ⋅=⇒
Recapitulando Gompertz propuso que yCBy ⋅=)(µ , y al sustituir este valor obtuvo que
xCx gKl ⋅=
Tiempo después Makeham propuso que yCBAy ⋅+=)(µ , donde A, era el factor de "azar"
( )∫ ⋅+−∫−
==⇒
xy
xdyCBAdyy
x elell 000
)(
0
µ
Resolvemos primero la integral:
⎥⎦⎤
⎢⎣⎡ −
∫∫∫ −−=⋅+−
1ln
000
)(
xCg
xy
xxy dyBCAdydyCBA
( ) [ ] [ ]110
0
lnln)( −− +⋅−=+=⋅+−⇒ ∫xx CCx
xy gxAgyAdyCBA
Sea SA ln−=−
[ ] [ ] [ ]111
0
lnlnlnln)( −−− ⋅=+⋅=+⋅−=⋅+−⇒ ∫xxx CxCC
xy gSgSxgxAdyCBA
[ ]10
ln)( −⋅=⋅+−⇒ ∫xCx
xy gSdyCBA
[ ]10
ln0
)(
0
)(
0
100 −⋅∫ ⋅+−∫−
⋅⋅====⇒⎥⎦⎤
⎢⎣⎡ − xxCx
xy
x
CxgSdyCBAdyy
x gSlelelellµ
[ ] xx
x CxC
xCxx gS
gl
ggSlgSll ⋅⋅=⋅⋅=⋅⋅=⇒ − 0
01
0
Sea gl
K 0=
xCxx gSKl ⋅⋅=⇒
Esta ultima formula es conocida como la ley de Gompertz –Makeham

23
Hasta aquí, hemos descubierto aquel modelo matemático que nos describe a la función lx en forma continua, pero, cómo se calculan los parámetros K, S, G y C? Esta pregunta la resolveremos usando el “Método de los Grupos no Superpuestos” Calculo de los parámetros de la ley de Gompertz-Makeham.
Método de los Grupos Superpuestos.
Se parte del hecho de tener i = 16 observaciones de la serie xl de la tabla de mortalidad distribuidas de igual forma en el tiempo.
m i x lx
1
1 5 95774 2 10 95659 3 15 95573 4 20 95391
2
5 25 95153 6 30 94792 7 35 94367 8 40 93638
3
9 45 92581 10 50 90870 11 55 87880 12 60 83975
4
13 65 78429 14 70 69603 15 75 57732 16 80 43043
Con las 16 observaciones se hacen m = 4 grupos de igual tamaño. Y se hace el siguiente
análisis: Partimos de la ley de Gompertz-Makeham xCx
x gSKl ⋅⋅=
Se hace una reetiquetación de la serie xl como se muestra en la columna "i" (Ej. Si i=1
entonces estaremos hablando de 5l ). Entonces la formula nos queda de la siguiente manera: iCi gSKil ⋅⋅=)(
)ln())(ln(iCi gSKil ⋅⋅=⇒
gCSiKil i lnlnln))(ln( ⋅+⋅+=⇒ Analizamos y sumando cada uno de los 4 grupos, tenemos que:
∑∑∑∑====
⋅+⋅+==⇒m
i
im
i
m
i
m
igCSiKilS
11110 lnlnln))(ln(
∑∑∑∑+=+=+=+=
⋅+⋅+==⇒m
mi
im
mi
m
mi
m
migCSiKilS
2
1
2
1
2
1
2
11 lnlnln))(ln(
∑∑∑∑+=+=+=+=
⋅+⋅+==⇒m
mi
im
mi
m
mi
m
migCSiKilS
3
12
3
12
3
12
3
122 lnlnln))(ln(
∑∑∑∑+=+=+=+=
⋅+⋅+==⇒m
mi
im
mi
m
mi
m
migCSiKilS
4
13
4
13
4
13
4
133 lnlnln))(ln(
Resolviendo estas sumas, tenemos que:
gcccSmmKmilSmm
iln
1ln
2)1(ln))(ln(
1
10 ⋅
−
−+⋅
++⋅==⇒
+
=∑
gccccsmmmKmilSm
mm
miln
1ln
2)1(ln))(ln(
12
2
11 ⋅⎟⎟
⎠
⎞⎜⎜⎝
⎛
−
−+⋅⎟
⎠
⎞⎜⎝
⎛ +++⋅==⇒
+
+=∑
gccccSmmmKmilSm
mm
miln
1ln
2)1(2ln))(ln(
122
3
122 ⋅⎟⎟
⎠
⎞⎜⎜⎝
⎛
−
−+⋅⎟
⎠
⎞⎜⎝
⎛ +++⋅==⇒
+
+=∑
Sacando diferencias tenemos que:
( ) gccccSmSSSm
m ln1
1ln1
2010 ⋅⎟⎟
⎠
⎞⎜⎜⎝
⎛
−
−−+⋅=−=Δ⇒
+
( ) gcccccSmSSSm
mm ln1
1ln1
2121 ⋅⎟⎟
⎠
⎞⎜⎜⎝
⎛
−−
−+⋅=−=Δ⇒+
( ) gcccccSmSSSm
mm ln1
1ln1
22232 ⋅⎟⎟
⎠
⎞⎜⎜⎝
⎛
−−
−+⋅=−=Δ⇒+
( ) gccccSSSm
m ln1
11
2010
2 ⋅⎟⎟⎠
⎞⎜⎜⎝
⎛
−−
−=Δ−Δ=Δ⇒+

24
( ) gcccccSSSm
mm ln1
11
2121
2 ⋅⎟⎟⎠
⎞⎜⎜⎝
⎛
−−
−=Δ−Δ=Δ⇒+
De 12SΔ se puede despejar "c"…
m
SSc
1
021
2
⎟⎟⎠
⎞⎜⎜⎝
⎛
ΔΔ
=⇒
De 02SΔ se puede despejar "g"…
⎪⎪
⎭
⎪⎪
⎬
⎫
⎪⎪
⎩
⎪⎪
⎨
⎧
⎟⎟⎠
⎞⎜⎜⎝
⎛
−−
−
Δ=⇒
+
cccc
Sgm
m
1)1(
exp1
2
02
De 0SΔ se puede despejar "a"…
⎪⎭
⎪⎬⎫
⎪⎩
⎪⎨⎧
⎥⎦
⎤⎢⎣
⎡⎟⎟⎠
⎞⎜⎜⎝
⎛
−−
−−Δ=⇒+
gccccS
mS
mm ln
1)1(1exp
1
02
De 0S se puede despejar "k"…
⎪⎭
⎪⎬⎫
⎪⎩
⎪⎨⎧
⎥⎦
⎤⎢⎣
⎡⎟⎟⎠
⎞⎜⎜⎝
⎛
−−
−⋅+
−=⇒+
gcccSmmS
mk
m
ln1
ln2
)1(1exp1
0
(Tarea, Dado lo anterior encuentre la formula para calcular los parámetros de la ley Gompertz) (Tarea, Dado el cuadro puesto al principio de este capitulo encuentre los parámetros de la Ley Gompertz-Makeham) Una de las tantas aplicaciones que se le puede dar a Gompertz es la Tabla de decrementos Múltiples.
7. TABLA DE DECREMENTOS MULTIPLES. En el repaso que se dio al principio se mencionaba el tema de “tabla de mortalidad”, la cual como recordaremos, estudiaba a un grupo cerrado de personas y cómo este grupo iba desapareciendo a través del tiempo por una causa, la de morir. En general un grupo de personas puede estar expuesto a salir del grupo por muchas causas, como por ejemplo, supongamos que tenemos a un grupo cerrado de personas en México, y se quiere estudiar cómo va desapareciendo dicho grupo de personas a través del tiempo, a saber hay dos causas por las cuales este grupo puede desaparecer, una es que las personas dejen el grupo por mortalidad, y la otra es que dejen el grupo por migración. Una Tabla de Decrementos Múltiples es, un cuadro estadístico que estudia a un grupo cerrado de personas y como éste desaparece a través del tiempo por k causas de salida del grupo. Para poder hacer dicho análisis es necesario definir lo siguiente:
• )(T
xl : Número de personas vivas de edad exacta “x” sujetas a salir del grupo por cualquiera de las “m” causas de salida.
• )(k
xd : Número de personas que dejan el grupo la causa “k” entre las edades x y x+1
• )(T
xd : Número de personas que dejan el grupo por cualquier causa entre las edades x y x+1, es decir:
•
∑=
=++++=m
k
kx
mxxxx
Tx dddddd
1
)()()3()2()1()(
Por otro lado tenemos que:
)()()(1
Tx
Tx
Tx dll −=+
• )(T
xq : Probabilidad de que una persona deje el grupo entre las edades x y x+1 por cualquier causa.
∑∑
=
= =+++===m
k
kxT
x
mx
Tx
xTx
xTx
m
k
kx
Tx
Txk
x qld
ld
ld
l
d
ld
q1
)()(
)(
)(
)2(
)(
)1(
)(1
)(
)(
)()(
Todos estos resultados son ciertos siempre y cuando se cuenten con tablas de decrementos simples “limpias”, es decir, siempre y cuando estemos seguros que todas las probabilidades

25
de salida del grupo no estén sobre estimadas o subestimadas, para poner en claro supongamos este ejemplo: De 100 personas que hay en México, supongamos que 10 de ellas fallecen, 5 migran de manera legal, y 5 de ellas migran de manera ilegal, es decir, nadie se entera que dejaron el país, al fin y al cabo nosotros tendríamos que de 100 personas en un determinado tiempo solo quedaron 80, y supondríamos que 15 fallecieron (10 que realmente fallecieron más 5 que migraron ilegalmente) y solo 5 migraron, de esta manera estaremos sobre estimando la probabilidad de muerte y subestimando la probabilidad de migración. Dado que en la práctica no hay tablas de decrementos simples limpias, es necesario hacer un ajuste a las probabilidades de salida del grupo, este ajuste se hace de dos formas: en base a la tasa instantánea de mortalidad (visto con Gompertz), y en base a la tasa centrales de mortalidad. AJUSTE DE LAS PROBABILIDADES DE SALIDA DEL GRUPO PARA UNA TABLA DE DECREMENTOS MULTIPLES POR MEDIO DEL MÉTODO DE LAS TASAS INSTANTANEAS (GOMPERTZ) Recordemos:
dxld
ldxld
l
Tx
Tx
Tx
x
xx
)(1)(1 )(
)()(
)( ⋅−=⇒⋅−= µµ
Por otro lado es importante hacer notar que para asegurar que no vamos a subestimar o sobreestimar alguna probabilidad es necesario que:
)()3()2()1(
1
)()( ... mxxxx
m
k
kx
Tx llllll ++++==∑
=
Substituyendo esto:
)()3()2()1(
)(
)(
)2(
)(
)1(
)(
1
)(
)(
)(
)()(
...
)(1.....)(1)(1
)(1)(1
mxxxx
mx
Tx
xTx
xTx
m
k
kx
Tx
Tx
Tx
Tx
dxld
ldxld
ldxld
l
dx
ld
ldxld
l
µµµµ
µ
++++=
⋅−−−⋅−⋅−=
=⋅−=⋅−=∑=
Por otro lado...
( )
( ) ( ))()3()2()1(
1)2(
1)1(
1)()2()1()(
1)()(
)()(
)(1
1)(
)(
)(1)()(
1
1)(
1)(
1)(
)()(
)()(
...
...expexp
...exp
exp
exp
ln)ln()ln(
))(ln(
))(ln()(1
mXXXX
x
xy
x
xy
x
x
myyy
TX
x
x
Ty
TX
TXT
X
TX
x
x
Ty
TX
TXT
XTX
x
x
Ty
x
x
Ty
x
x
Ty
Ty
Ty
Ty
Ty
PPPP
dydy
dyP
dyP
Plldy
lllldy
dylddy
dyld
dyld
l
⋅⋅⋅⋅=
⋅⎭⎬⎫
⎩⎨⎧−⋅
⎭⎬⎫
⎩⎨⎧−=
⎭⎬⎫
⎩⎨⎧
+++−=⇒
⎭⎬⎫
⎩⎨⎧−=⇒
==⎭⎬⎫
⎩⎨⎧−⇒
⎟⎟⎠
⎞⎜⎜⎝
⎛=−=−⇒
=−⇒
−=⋅−=
∫∫
∫
∫
∫
∫
∫∫
++
+
+
++
++
+
++
µµ
µµµ
µ
µ
µ
µ
µ
De esta última igualdad tenemos:
( ) ( ) ( )( ) ( ) ( ) ( ))'()'2()'1()()2()1(
)()2()1()(
)()3()2()1()(
1...11...1
1...111
...
mXXX
mXXX
mXXX
TX
mXXXX
TX
qqqqqqqqqq
PPPPP
−⋅⋅−⋅−=+++−⇒
−⋅⋅−⋅−=−⇒
⋅⋅⋅⋅=
Donde:
• )(k
xq : son las probabilidades ajustadas
• )'(k
xq : son las probabilidades observadas Por poner un ejemplo supongamos que m=3
( ) ( ) ( ) ( ))'3()'2()'1()'3()'2()'3()'1()'2()'1()'1()'1()'1(
)'3()'2()'1()3()2()1(
1
1111
XXXXXXXXXXXX
XXXXXX
qqqqqqqqqqqqqqqqqq
−+++−−−=
−⋅−⋅−=++−

26
Es decir:
)'3()'2()'1()'3()'2()'3()'1()'3(
)'3()'2()'1()'3()'2()'3()'1()'2(
)'3()'2()'1()'3()'1()'2()'1()'1(
)'3()'2()'1()'3()'2()'3()'1()'2()'1()'1()'1()'1()3()2()1(
31
21
21
31
21
21
31
21
21
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXXXXXXXXX
qqqqqqqq
qqqqqqqq
qqqqqqqq
qqqqqqqqqqqqqqq
+−−+
+−−+
+−−=
+−−−++=++
Finalmente distribuyendo esta suma unifórmenle:
)'3()'2()'1()'3()'2()'3()'1()'3()3(
)'3()'2()'1()'3()'2()'3()'1()'2()2(
)'3()'2()'1()'3()'1()'2()'1()'1()1(
31
21
21
31
21
21
31
21
21
XXXXXXXXX
XXXXXXXXX
XXXXXXXXX
qqqqqqqqq
qqqqqqqqq
qqqqqqqqq
+−−=
+−−=
+−−=
(Tarea: Encontrar la relación entre las tasas ajustadas y observadas para 4 causas de salida del grupo) (Tarea: construir una tabla de decrementos múltiples) (Tarea: Encontrar una formula general de la relación entre tasas ajustadas y observadas) AJUSTE DE LAS PROBABILIDADES DE SALIDA DEL GRUPO PARA UNA TABLA DE DECREMENTOS MULTIPLES POR MEDIO DEL MÉTODO DE LAS TASAS CENTRALES. Usando las mismas definiciones:
• )(T
xl : Número de personas vivas de edad exacta “x” sujetas a salir del grupo por cualquiera de las “m” causas de salida.
• )(k
xd : Número de personas que dejan el grupo la causa “k” entre las edades x y x+1
• )(T
xd : Número de personas que dejan el grupo por cualquier causa entre las edades x y x+1, es decir:
∑=
=++++=m
k
kx
mxxxx
Tx dddddd
1
)()()3()2()1()(
Por otro lado tenemos que: )()()(
1Tx
Tx
Tx dll −=+
• )(k
xq : Probabilidad de que una persona deje el grupo entre las edades x y x+1 por la causa “k”.
∑∑
=
= =+++===m
k
kxT
x
mx
Tx
xTx
xTx
m
k
kx
Tx
Txk
x qld
ld
ld
l
d
ld
q1
)()(
)(
)(
)2(
)(
)1(
)(1
)(
)(
)()(
Pero ahora definiremos nuevas funciones:
• )( k
xd−
: Número de personas que dejan el grupo por una causa diferente de “k” entre las edades x y x+1.
∑≠=
−− =m
kii
ix
kx dd
1
)()(
• )( k
xq−
: Probabilidad de que una persona deje el grupo entre las edades x y x+1 por una causa diferente de “k”.
Tx
kxk
x ld
q)(
)(−
− =
Ahora bien recordemos que en el caso anterior, esto solo funciona en teoría, es decir, puede darse el caso de que las probabilidades de decrementos simples estén sobreestimada o subestimada, por lo que para construir una tasa de decremento simple mas apegada a la realidad se tendría que tener:
)(
)()(' k
x
kxk
x ld
q =
Es decir, las muertes ocurridas por la causa “k” entre el total de personas expuestas a salir
del grupo solo por la causa k, pero, ¿quién es )(k
xl ?. Bueno, esta se puede estimar restándole
a )(T
xl todas aquellas personas que salieron del grupo por causa distinta de “k”:
)()()(
21 k
xTx
kx dll −−=

27
Nótese que a las personas que dejaron el grupo por causa diferente de “k” se multiplicaron por un medio, esto suponiendo que se da una distribución uniforme de salida del grupo en el lapso de un año. Con esto último podemos obtener una relación entre tasas ajustadas y observadas. Es decir:
)(
)(
)(
)(
)(
)(
)(
)(
)()(
)(
)(
)()(
211
21
21
'k
x
kx
Tx
kx
Tx
Tx
Tx
kx
kx
Tx
kx
kx
kxk
x
q
q
ld
ll
ld
dl
dld
q−
−− −
=
−
=−
==
Por lo tanto:
)(
)()(
211
'k
x
kxk
x
q
−−=
En donde como en el caso anterior las tasas que tienen apostrofe son las tasas observadas y las que no tienen apostrofe son las ajustadas. Ahora bien para ejemplificar lo anterior, supongamos que tenemos solo 3 causas de salida del grupo, es decir m = 3, entonces:
( ))3()2(
)1()1(
211
'xx
xx
+−=
; ( ))3()1(
)2()2(
211
'xx
xx
+−=
;
( ))2()1(
)3()3(
211
'xx
xx
+−=
O dicho de otra manera si trabajamos para la causa 1:
( ) )3()1()2()1()1()3()2()1()1( '21'
21'
211' xxxxxxxxx qqqqqqqqq −−=⎟
⎠
⎞⎜⎝
⎛ +−=
Finalmente:
)3()1()2()1()1()1( '21'
21' xxxxxx qqqqqq ++=
Y para las otras dos causas:
)2()3()1()3()3()2(
)3()2()1()2()2()2(
'21'
21'
'21'
21'
xxxxxx
xxxxxx
qqqqqq
qqqqqq
++=
++=
Ahora bien hay que notar que tenemos entonces un sistema tres ecuaciones con tres incógnitas, es decir:
)2()3()1()3()3()2(
)3()2()1()2()2()2(
)3()1()2()1()1()1(
'21'
21'
'21'
21'
'21'
21'
xxxxxx
xxxxxx
xxxxxx
qqqqqq
qqqqqq
qqqqqq
++=
++=
++=
Tal ves no es claro ver el sistema de ecuaciones, por lo que hay que acomodarlo:
)3()2()3()1()3()2(
)3()2()2()1()2()2(
)3()1()2()1()1()1(
'21'
21'
'21'
21'
'21'
21'
xxxxxx
xxxxxx
xxxxxx
qqqqqq
qqqqqq
qqqqqq
++=
++=
++=
En donde desconozco las tasas ajustadas )3()2()1( ,, xxx qqq , y todo lo demás si lo conozco por
lo que solo resta resolver el sistema de ecuaciones:
1'21'
21
'211'
21
'21'
211
1'21'
'211'
'21'
21'
)3()3(
)2()2(
)1()1(
)3()3(
)2()2(
)1()1()1(
)1(
xx
xx
xx
xx
xx
xxx
x
qqq
q = ;
1'21'
21
'211'
21
'21'
211
1''21
'21''
21
'21'1
)3()3(
)2()2(
)1()1(
)3()3(
)2()2()2(
)1()1(
)2(
xx
xx
xx
xx
xxx
xx
x
qqq
q =
Y finalmente:

28
1'21'
21
'211'
21
'21'
211
''21'
21
'1'21
''211
)3()3(
)2()2(
)1()1(
)3()3()3(
)2()2(
)1()1(
)3(
xx
xx
xx
xxx
xx
xx
x
qqq
q =
Faltaría solo resolver los determinantes para llegar a una formula general que relacione las tasas ajustadas y observadas de una tabla de decrementos múltiples para tres causas. (Tarea: Encontrar la relación entre las tasas ajustadas y observadas para 4 causas de salida del grupo) (Tarea: construir una tabla de decrementos múltiples) (Tarea: Encontrar una formula general de la relación entre tasas ajustadas y observadas)






![Aeropuerto Arr[1][1][1][1][1][1][1][1].](https://static.fdocuments.es/doc/165x107/58f32d261a28ab9c018b45a3/aeropuerto-arr11111111.jpg)

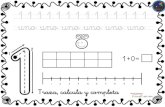



![La%252525252520 selección%252525252520española[1][1][1][1][1][1]](https://static.fdocuments.es/doc/165x107/555b87d2d8b42acd238b497c/la252525252520-seleccion252525252520espanola111111.jpg)



![CINCO RECO DS MUNDIALEShemeroteca-paginas.mundodeportivo.com/./EMD02/HEM/... · 3treoIes, 1 d fetxero de I91;1] MatacicCJdma;0] CINCO RECO DSMUNDIALES 1 1 1 1 1 1 1 1 1 1 1 1 1 1](https://static.fdocuments.es/doc/165x107/5f80ffd681d4d0156c04141b/cinco-reco-ds-mundialeshemeroteca-3treoies-1-d-fetxero-de-i911-mataciccjdma0.jpg)
![Suficienteparavivir 1 _1__1_[1][1][1][1][1].](https://static.fdocuments.es/doc/165x107/55a00c741a28ab44568b484c/suficienteparavivir-1-1111111.jpg)
