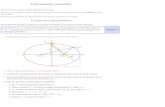
Elipse
4
Historia La elipse, como curva geométrica, fue estudiada por Menecmo, investigada por Euclides, y su nombre se atribuye a Apolonio de Perge. El foco y la directriz de la sección cónica de una elipse fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era ovalada, aunque más tarde descubrió que se trataba de una elipse con el Sol en un foco. De hecho, Kepler introdujo la palabra «focus» y publicó su descubrimiento en 1609.Halley, en 1705, demostró que el cometa que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol. 2 Elipse La elipse es una línea curva, cerrada y plana cuya definición más usual es: La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante. Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de revolución. 1 Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras que una elipse que gira alrededor de su eje principal genera un esferoide alargado. Ecuaciones de la elipse En coordenadas cartesianas Forma cartesiana centrada en el origen La ecuación de una elipse en coordenadas cartesianas , con centro en el origen, es: donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de las abscisas y b al eje de las ordenadas la elipse es horizontal, si es al revés, entonces es vertical. El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2εa, siendo ε la excentricidad y a el semieje mayor . Forma cartesiana centrada fuera del origen Si el centro de la elipse se encuentra en el punto (h,k), la ecuación es:
Transcript of Elipse
Historia La elipse, como curva geométrica, fue estudiada por Menecmo, investigada por Euclides, y su
nombre se atribuye a Apolonio de Perge. El foco y la directriz de la sección cónica de una elipse
fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era ovalada, aunque
más tarde descubrió que se trataba de una elipse con el Sol en un foco. De hecho, Kepler introdujo
la palabra «focus» y publicó su descubrimiento en 1609.Halley, en 1705, demostró que el cometa
que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol.2
Elipse La elipse es una línea curva, cerrada y plana cuya definición más usual es:
La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias
a otros dos puntos fijos llamados focos es constante.
Una elipse es la curva simétrica cerrada que resulta al cortar la superficie de un cono por un plano
oblicuo al eje de simetría –con ángulo mayor que el de la generatriz respecto del eje de
revolución.1 Una elipse que gira alrededor de su eje menor genera un esferoide achatado, mientras
que una elipse que gira alrededor de su eje principal genera un esferoide alargado.
Ecuaciones de la elipse En coordenadas cartesianas
Forma cartesiana centrada en el origen
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse, donde si a corresponde al eje de
las abscisas y b al eje de las ordenadas la elipse es horizontal, si es al revés, entonces es vertical.
El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia
focal y vale 2c = 2εa, siendo ε la excentricidad y a el semieje mayor.
Forma cartesiana centrada fuera del origen
Si el centro de la elipse se encuentra en el punto (h,k), la ecuación es:
En coordenadas polares
Forma polar centrada en origen
En coordenadas polares, con origen en su centro, la ecuación de la elipse es:
(epc 1)
Una ecuación más elegante que la anterior (pero que obliga a pre-calcular la
excentricidad ), es:
(epc 2)
Para ambas ecuaciones a es el semieje mayor, b es el semieje menor de la elipse, θ es el ángulo
polar y para la (epc 2) ε es la excentricidad.
Si no se quiere pre-calcular la excentricidad convendrá utilizar la ecuación (epc 1), en
caso contrario utilizar la ecuación (epc 2).
Formas polares centradas en un foco
Coord. polares sobre un foco.
En coordenadas polares, con el origen en el foco F2, la ecuación de la elipse es:
(501)
Para el foco F1:
(502)
"Semi-latusrectum" (en verde) de la elipse.
En el caso un poco más general de una elipse con el foco F2 en el origen y el otro foco en la
coordenada angular , la forma polar es:
(503) }
El ángulo de las ecuaciones (501),(502) y (503) es la llamada anomalía verdadera del punto y el
numerador de las mismas es el llamado semi-latusrectum de la elipse, normalmente
denotado . El semi-latusrectum es la distancia entre un foco y la misma elipse sobre una línea
perpendicular al semieje mayor que pasa por el foco.
Formas paramétricas
La ecuación paramétrica de una elipse con centro en y siendo el semieje mayor y el
menor, es:
con no es el ángulo θ del sistema de coordenadas polares con origen en el
centro de la elipse, sino la anomalía excéntrica de la elipse. La relación entre y θ es
.
La ecuación paramétrica de una elipse con centro en en la que el parámetro sea
concordante con el ángulo polar respecto al centro desplazado es:
con . El parámetro es el ángulo de un sistema polar cuyo origen está centrado
en .
Área interior de una elipse
El área de la superficie interior de una elipse es:
Siendo a y b los semiejes.4
Perímetro de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda
especie.
Sin embargo, el matemático Ramanujan dio una expresión sencilla que se aproxima
razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante
integrales elípticas. Ramanujan, en su fórmula, utiliza el “semieje mayor” (a) y el “semieje
menor” (b) de la elipse. Expresión aproximada del perímetro de una elipse:
Propiedades notables
La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver
en Analogía de Michelson y Morley.
