Espacio deFormaciónMultimodal

Tinoco, G. (2013). Ecuación de la elipse dados ciertos elementos. [Manuscrito no publicado]. México: UAEM.

Elipse: Ecuación de la elipse dados ciertos elementos

!!

!

! !!

"!"!

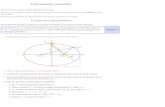
Elipse vertical !Si la elipse tiene centro en el origen y sus focos están sobre el eje y , las

coordenadas de ellos son ( )0,F c y

( )' 0,F c! . De manera similar se

denomina 2a a la suma de las

distancias de un punto ( ),P x y de la

elipse a los focos. Si se hace un análisis semejante al caso de la elipse horizontal, o simplemente se

intercambian los papeles de las variables, se llega a la siguiente ecuación: 2 2

2 2 1x yb a

+ =

En donde, al igual que en el caso anterior 2 2 2b a c= !

Los vértices son, en este caso ( ) ( )' 0, , 0,A a A a! . Esto es, el eje mayor de la elipse se

encuentra sobre una recta vertical (el eje focal) y el eje menor se encuentra sobre una recta horizontal (eje secundario).

Excentricidad

Si se comparan las gráficas de dos elipses, por ejemplo:

2 2

116 4x y

+ =

2 2

181 9x y

+ =

Se observa que una de ellas es más “alargada” que la otra. Este alargamiento de la elipse se mide mediante un cociente

denominado cea

= .

En la primera ecuación, 4a = y 2b = , 16 4 12c = ! = , entonces:

12 0.864

cea

= = !

!!

!

! !!

#!#!

En segunda ecuación, 9a = y 3b = , 81 9 72c = ! = , entonces:

72 0.949

cea

= = !

En la elipse que es más “alargada” el cociente e es mayor. Este cociente que mide el “alargamiento” de una elipse se denomina excentricidad, la cual se define como la razón

entre la distancia focal y el eje mayor, esto es: 22c cea a

= =

En el caso de la elipse c a< siempre, entonces 0 1e< < . Cuanto más cercano a cero sea el valor de la excentricidad, la elipse será más parecida a un círculo, y cuanto más se acerque a 1, la elipse será más “alargada”. Cuando 0e = es porque 0c = , esto significa que los dos focos están en el mismo lugar y los dos semiejes son iguales, por lo tanto, se tiene un círculo.

Elipse con centro fuera del origen

Elipse horizontal Si el centro de la elipse no es el origen del sistema de coordenadas, sino un punto ( ),C h k

y el eje focal es paralelo al eje x , dado que llamamos 2c a la distancia focal, entonces las

coordenadas de los focos son ( ),F h c k+ y

( )' ,F h c k! .

Para determinar la ecuación se toma como base la ecuación de la elipse centrada en el origen, y se utiliza un segundo sistema de ejes cuyo origen 'O coincide con el centro de la elipse.

En el nuevo sistema de coordenadas, la ecuación

de la elipse es: ( ) ( )2 2

2 2

' '1

x ya b

+ = . En esta

ecuación se sustituyen 'x y 'y por sus equivalentes de acuerdo a las fórmulas de la traslación, ' 'x x h y y k= ! = ! . El resultado es la forma estándar de la ecuación de una elipse horizontal con centro fuera del origen.

!!

!

! !!

$!$!

( ) ( )2 2

2 2 1x h y ka b! !

+ =

Elipse vertical En el caso de que el eje focal sea vertical, la forma estándar de la ecuación es similar a la ecuación de la elipse horizontal, simplemente se intercambian los denominadores.

( ) ( )2 2

2 2 1x h y kb a! !

+ =

Los vértices son, en este caso ( )' ,A h k a! y ( ),A h k a+ . El eje mayor de la elipse se

halla ahora sobre una recta vertical (eje focal), y el eje menor sobre una recta horizontal (eje secundario).

Forma estándar de la ecuación Para determinar la ecuación de una elipse se requiere saber si la elipse es horizontal o vertical, conocer las coordenadas de su centro y la medida de sus semiejes (semieje mayor a y semieje menor b ).

Ejemplo: Determinar la ecuación de la elipse horizontal que tiene su centro en el punto

( )3, 10C ! , su semieje mayor es: 6a = y su semieje menor es: 11b = .

Se sustituyen los datos en la forma estándar de la ecuación, y se simplifica.

( ) ( )

( )( ) ( )( )( )

( ) ( )

2 2

2 2

2 2

22

2 2

1

3 101

6 11

3 101

36 11

x h y ka b

x y

x y

! !+ =

! ! !+ =

! ++ =

Nota: La tarea de determinar la forma estándar de la ecuación de una elipse se puede practicar en la aplicación "Ecuación de la elipse (1)" del capítulo "Elipse", disponible en la dirección:

http://www.geogebratube.org/student/c6961/m67380/ylyy

!!

!

! !!

%!%!

Elementos de la elipse dada su ecuación. A partir de la forma estándar de la ecuación se pueden determinar todos los elementos de una elipse y trazar su representación gráfica.

Ejemplo: Determinar los elementos de la elipse ( ) ( )2 21 6

116 100x y+ +

+ = .

1x h x! = + , por lo tanto: 1h! = y entonces 1h = ! .

6y k y! = + , por lo tanto: 6k! = y entonces 6k = ! .

por lo que, el centro es: ( )1, 6C ! ! .

2 100a = , por lo tanto: 100 10a = = .

2 16b = , por lo tanto: 16 4b = = .

La semidistancia focal es:

2 2 2

2 2 100 16 84 2 21

a b c

c a b

= +

= ! = ! = =

El valor de la excentricidad es: 2 21 2110 5

cea

= = =

La medida del lado recto es: ( )2 2 162 32 1610 10 5

bLra

= = = =

Los vértices son: ( ) ( )1, 6 10 , ' 1, 6 10A A! ! + ! ! !

Simplificando: ( ) ( )1, 4 , ' 1, 16A A! ! !

Los covértices son: ( ) ( )1 4, 6 , ' 1 4, 6B B! + ! ! ! !

Simplificando: ( ) ( )3, 6 , ' 5, 6B B! ! !

Los focos son los puntos: ( ) ( )1, 6 2 21 , ' 1, 6 2 21F F! ! + ! ! !

Nota: La tarea de determinar los elementos y la representación gráfica de una elipse, dada la forma estándar de su ecuación, se puede practicar en la aplicación interactiva "Gráfica y elementos de una elipse (1)"

del capítulo "Elipse" disponible en la dirección: http://www.geogebratube.org/student/c6961/m67380/ylyy