Capıtulo 1

Grafos

1.1. Definiciones Basicas y Ejemplos

Definicion 1.1.1. Un grafo simple G es un par (V, E) donde

V es un conjunto finito cuyos elementos se denominan vertices. Llamaremos ordende G al numero de vertices y lo denotaremos por |V |.

E es un subconjunto finito de V × V , tal que si (a, b) ∈ E, entonces a 6= b y(b, a) ∈ E. Los elementos de E se denominan aristas.

Si (a, b) ∈ E, debido a que (a, b) ∈ E ⇐⇒ (b, a) ∈ E, denotamos la arista que conectaa y b como {a, b}. Se dice que los vertices a y b son adyacentes cuando estan conectadospor una arista y los vertices a y b se denominan extremos de la arista.

Graficamente representaremos los vertices por puntos y las aristas por lıneas que losunen. En los grafos simples, dos vertices, si son adyacentes, estan unidos por una unicaarista

Ejemplo:El siguiente grafico representa un grafo con tres vertices y tres aristas:

Nosotros hemos dado la definicion de un grafo simple, pero tambien existen otro tipode grafos como:

3

4 CAPITULO 1. GRAFOS

Multigrafo Grafo en donde dos vertices distintos pueden estar unidos por mas de unaarista. Dos o mas aristas que unen el mismo par de vertices distintos se denominanmultiaristas.

Pseudografo Una arista puede conectar un mismo vertice. Una arista que conecta unmismo vertice se denomina lazo.

Digrafo Un grafo en el cual las aristas son pares ordenados. Es decir, (a, b) 6= (b, a).Graficamente, la arista (a, b) se representa con una flecha dirigida de a a b.

Ejemplo:El grafo de la derecha es un multigrafo, y el de la izquierda es un pseudografo.

Otra

x y

Multiarista

lazo

Cuadro 1.1: Grafos no simples

A lo largo de este curso nos centraremos en los grafos simples, por lo tanto, la palabragrafo implicara grafo simple si no se indica lo contrario.

Definicion 1.1.2. Llamaremos grado de un vertice al numero de aristas de las que esextremo. Se dice que un vertice es ’par’ o ’impar’ segun lo sea su grado.

Ejemplo:En este grafo, el vertice 5 tiene grado cuatro, y los demas grado uno.

Dado un conjunto, podrıamos hablar de subconjuntos; dado un retıculo, podrıamoshablar de retıculos, y dado un grafo, tambien podremos hablar de subgrafos.

Definicion 1.1.3. Sea G = (V,E) un grafo. Un subgrafo de G es otro grafo G′ = (V ′, E ′),tal que V ′ ⊆ V , E ′ ⊆ E y si {a, b} ∈ E ′, entonces a, b ∈ V ′.

A la hora de representar un grafo simple, existen mas herramientas que su grafico,como la matriz de adyacencia

1.1. DEFINICIONES BASICAS Y EJEMPLOS 5

2

13

4

5

Cuadro 1.2:

Definicion 1.1.4. Sea G un grafo de orden n. La matriz de adyacencia de G es una lamatriz con n filas y n columnas, denotada A = (aij), donde aij = 1 si los vertices i y json adyacentes y aij = 0 en otro caso.

La matriz de adyacencia de un grafo simple siempre es simetrica, es decir, aij = aji, ysu diagonal es nula.

Ejemplo:La matriz de adyacencia del grado de la figura 1.2 es:

v1 v2 v3 v4 v5

v1

v2

v3

v4

v5

0 0 0 0 10 0 0 0 10 0 0 0 10 0 0 0 11 1 1 1 0

1.1.1. Caminos y conexidad

Supongamos que tenemos un grafo G y dos de sus vertices x, y. Una de las preguntasque se pueden plantear es si a traves de las aristas del grafo, se puede ir desde el verticex al vertice y, es decir, si hay un camino que conecta x con y.

Otra

x y

6 CAPITULO 1. GRAFOS

Definicion 1.1.5. Sean x, y ∈ V , se dice que hay un camino en G de x a y si existe unasucesion finita no vacıa de aristas

{x, v1}, {v1, v2}, ..., {vn, y}.

Si hay camino de x a y, entonces

los vertices x a y se llaman los extremos del camino,

el numero de aristas del camino se denomina la longitud del camino,

si los vertices no se repiten el camino se dice propio o simple,

llamaremos sendero a un camino que nunca pasa dos veces por la misma arista,aunque pueda repetir vertices,

cuando los dos extremos de un camino son iguales, el camino se llama circuito ocamino cerrado,

llamaremos ciclo a un circuito simple, es decir, un camino con extremos igualesdonde el unico vertice que se repite es el inicial como punto de llegada,

llamaremos sendero cıclico a un sendero que es cerrado, es decir, un camino conextremos iguales donde no se repiten aristas,

el vertice y se dice accesible desde el vertice x si existe un camino entre ellos. Todovertice es accesible respecto a si mismo

Un ciclo de longitud k se llama k–ciclo.

Observad que si hay un camino entre 2 vertices, tambien habra un camino simple entreellos.

Definicion 1.1.6. Un grafo G es conexo si cada par de vertices esta unido al menos porun camino.

Un grafo que no es conexo se denomina desconexo. Cada grafo desconexo se puededesglosar en un numero de subgrafos conexos, cada unos de los cuales es una componenteconexa del grafo.

1.1. DEFINICIONES BASICAS Y EJEMPLOS 7

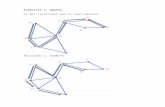
Ejemplo:En el grafo de la izquierda, observad que no hay camino entre el vertice x y el vertice y,por lo tanto no es conexo.

x

y

grafo noconexo

grafo conexo

2 componentesconexas

Definicion 1.1.7. Una arista de un grafo G se dice de separacion si G es conexo pero alsuprimir la arista, se divide en dos componentes conexos

Como ejemplo, el grafo del cuadro 1.2 es conexo y todas las aristas son de separacion.

′ f : G → G′ E′. En este caso, diremos queG y G′ V y los de V′