1

MÉTODO MATRICIAL

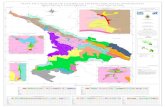
Introducción Utilizaremos el ejemplo de la figura como referencia para la exposición del Método Matricial. Aunque se trata de un caso bidimensional (2D), es suficiente para la explicación de los fundamentos del método. Al final del tema se expondrán las peculiaridades del caso tridimensional (3D). En los recuadros aparecen numerados los nudos (puntos de unión de dos o más barras). Y en cada nudo los tres grados de libertad correspondientes al plano. Los grados de libertad pueden referirse a desplazamientos y giros, o bien a fuerzas y momentos. A efectos de simplificar el lenguaje y la notación, en adelante diremos desplazamientos, entendiendo desplazamientos o giros indistintamente, y fuerzas, entendiendo fuerzas o momentos indistintamente. Tanto los desplazamientos como las fuerzas en los nudos, están referidos a los ejes X-Y (coordenadas globales). La expresión que relaciona las fuerzas con los desplazamientos es de la forma:

F=KU

donde K es la matriz de rigidez del sistema. El objetivo final del método es llegar a conocer todos los desplazamientos y, en función de los mismos, las solicitaciones en los extremos de cada barra. .

XL YL

X

Y

12

5 4

1

2

4

3

2

3

1

8

9

7 14

15

13

6

11

105

2

Para cada barra, consideraremos unos ejes XL-YL (coordenadas locales). La relación entre las fuerzas y los desplazamientos en los extremos de cada barra es de la forma:

FL=KLUL

donde KL es la matriz de rigidez de la barra en coordenadas locales. Posteriormente habrá que ensamblar barras; es decir, componer la estructura a partir de sus barras. Para ello es necesario que todas las fuerzas y todos los desplazamientos estén referidos a un mismo sistema de ejes. Para ello, una vez calculada la matriz de rigidez de cada barra en coordenadas locales, hemos de realizar una rotación para referir dicha matriz a coordenadas globales. De igual forma, las fuerzas y los desplazamientos han de quedar referidos a coordenadas globales. En cada nudo se han de cumplir las condiciones de equilibrio; para ello, la fuerza total en el nudo ha de ser la suma de las fuerzas que actúan sobre cada una de las barras que concurren en él. También se han de cumplir las condiciones de compatibilidad, por lo que el desplazamiento del nudo debe ser único, e igual al desplazamiento en ese punto de cada una de las barras concurrentes. Matriz de rigidez de una barra en coordenadas locales Los términos de la matriz KL son los coeficientes de rigidez kij, que relacionan la fuerza aplicada según el grado de libertad i con el desplazamiento según el grado de libertad j, en el supuesto de que los desplazamientos en los grados de libertad ≠j sean nulos. Así:

fi = kij uj expresa la fuerza que se produce en el grado de libertad i cuando realizamos un desplazamiento unitario según el grado de libertad j. Veámoslo sobre la barra de la figura, en la que consideramos los seis grados de libertad posibles: Consideremos j=1, produciendo un desplazamiento unidad según el eje X en el extremo izquierdo de la barra, uj=1. La barra experimenta un acortamiento, con lo que aparecen unas fuerzas de compresión.

XL

YL

1

2

3

5

6

4

1 2

3

Para deducir k11, de la ley de Hooke:

EAFLL =∆ ; L

LEAF ∆= ;

LEAk =11

De la expresión f4= k41u1 , considerando que es en 1 donde se produce el desplazamiento, resulta:

LEAk −=41

en concordancia con el criterio de signos elegido. El resto de las ki1 serán cero. Considerando ahora el grado de libertad 2 (j =2): j = 2, u2=1

En la figura se puede apreciar como se deformaría la barra, apareciendo unos momentos asociados la deformación, que son fácilmente calculables mediante las fórmulas de deformaciones en vigas. De:

∆= 2

6LEIM

para ∆=1, resulta:

f4f1= k11 u1

u1=1

u2=1

4

2326LEIk = y 262

6LEIk =

Con sólo esos momentos la barra no está en equilibrio. Considerando los demás grados de libertad, aparece un par que ha de equilibrar a los momentos.

∆== 3

122LEI

LMT

de donde:

32212

LEIk = y 352

12LEIk −=

Considerando grado de libertad j=3: Con esta deformada se producen unos momentos en los extremos:

M6= k62 u2M3= k32 u2

L

f2 = k22 u2 f5= k52 u2

MB MA

u3=1

5

Mediante las fórmulas de deformaciones en vigas:

∆=LEIM A

4 ∆=LEIM B

2

Y comparando con la notación empleada para el método matricial: Resulta:

LEIk 4

33 = y LEIk 2

63 =

Igual que en el caso anterior, vemos que no es una situación de equilibrio. Considerando los demás grados de libertad: De las expresiones de los momentos:

∑ ∆=LEIM 6

con lo cual, el valor de cada fuerza es:

LM

T ∑=

de donde:

2236LEIk = y 253

6LEIk −=

M6= k63 u3M3= k33 u3

L

f2 = k23 u3 f5= k53 u3

6

Como puede apreciarse, el término k23 es igual al k32, calculado antes. Esto es consecuencia de la simetría de la matriz KL (teorema de reciprocidad). Las consideraciones para el grado de libertad 4 son iguales que las del 1, excepto en los signos: resultando:

LEAk =44 y

LEAk −=14

El grado de libertad 5 es similar al 2, con la siguiente deformada: Y el 6 es análogo al 3: Finalizado el análisis de los grados de libertad de la barra considerada, resulta:

f4= k44 u4 f1= k14 u4

u4=1

u5=1

u6=1

7

KL

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

−

−−−

−

−

−

−

=

LEI

LEI

LEI

LEI

LEI

LEI

LEI

LEI

LAE

LAE

LEI

LEI

LEI

LEI

LEI

LEI

LEI

LEI

LAE

LAE

460260

61206120

0000

260460

61206120

0000

22

2323

22

232

De la simple inspección de esta matriz se puede apreciar que es singular de grado 3. Las fuerzas del vector FL no son independientes; por la forma en que se han obtenido, están relacionadas por las 3 condiciones de equilibrio en el plano. La barra considerada carece de ligaduras externas, por lo que será posible fijar arbitrariamente 3 de los términos de UL (por ejemplo, los desplazamientos en un extremo), por lo que UL, además de contener los desplazamientos relativos entre los dos extremos de la barra, incluye un desplazamiento de sólido rígido de la misma. Los inconvenientes que pudieran derivarse de estas circunstancias, quedarán resueltos como veremos más adelante. Rotación a ejes globales De la rotación de ejes en coordenadas cartesianas:

θθ senuuu L 211 cos += θθ cos212 usenuu L +−=

33 uu L =

X u1

u1L

u2LXL

u2

θ

Y

YL

8

Matricialmente:

⎥⎥⎥

⎦

⎤

⎢⎢⎢

⎣

⎡

⎥⎥⎥

⎦

⎤

⎢⎢⎢

⎣

⎡−=

⎥⎥⎥

⎦

⎤

⎢⎢⎢

⎣

⎡

3

2

1

3

2

1

1000cos0cos

uuu

sensen

uuu

L

L

L

θθθθ

Considerando los seis grados de libertad: la expresión completa de la rotación es:

⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

−

−

=

⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

6

5

4

3

2

1

6

5

4

3

2

1

1000000cos0000cos0000001000000cos0000cos

uuuuuu

sensen

sensen

uuuuuu

L

θθθθ

θθθθ

;

Matriz de rotación R De forma abreviada: UL=RU, y análogamente: FL=RF Sustituyendo estas expresiones en: FL=KLUL Resulta: RF=KLRU Premultiplicando esta expresión por RT, y considerando que: RT=R-1 (por ser 1 el valor del determinante de la matriz R), se verifica:

RTRF = RTKLRU

F = RTKLRU La relación entre fuerzas y desplazamientos en los extremos de la barra, en coordenadas globales es de la forma: F = KU. Comparándola con la expresión obtenida, resulta finalmente:

XL

YL

1

2

3

5

64

9

K = RTKLR.

donde K es la matriz de rigidez de la barra considerada, expresada en coordenadas globales. Nótese que la rotación de ejes no modifica el carácter singular de la matriz de rigidez. Ensamblaje de barras Una vez obtenida la matriz de rigidez de cada barra en coordenadas globales habrá que proceder a la operación de ensamblaje de barras, hasta definir la estructura a partir de las barras que la componen. Para facilitar la comprensión del método, comenzaremos por ensamblar dos barras. Consideremos las barras 1-2 y 2-3, representadas en la figura. En el nudo 2, común a ambas, el desplazamiento es único: u4, u5, u6. Las fuerzas que aparecen en el nudo como consecuencia de dicho desplazamiento son las que han de deformar la barra 1-2 más las que han de deformar la 2-3 (de acuerdo con la idea del método, recordemos: suponiendo nulos los desplazamientos en los nudos 1 y 3). Para la barra 1-2, de matriz de rigidez K12, dichas fuerzas vienen definidas por la submatriz de filas 4,5,6 y columnas 4,5,6 (producto de dicha submatriz de K12 por el vector: u4, u5, u6). Análogamente, para la barra 2-3, de matriz de rigidez K23, las fuerzas correspondientes vienen definidas por la submatriz de filas 4,5,6 y columnas 4,5,6 de la matriz K23. Para expresar las fuerzas F4, F5, F6 en el conjunto de ambas barras, bastará sumar los términos comunes a las dos submatrices anteriores (zona cuadriculada en la figura). Queda así definida una matriz de orden 9×9 que relaciona los desplazamientos según los 9 grados de libertad del conjunto con las fuerzas correspondientes. Dicha matriz es la matriz de rigidez del conjunto de las dos barras.

3

1

2

1

5 4 2

6

3

8

9

7

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

=

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

9

8

7

6

5

4

3

2

1

9

8

7

6

5

4

3

2

1

uuuuuuuuu

FFFFFFFFF

K12

K23

1

2

3

1

2

3

10

A efectos de terminología, a la operación de superponer matrices y sumar los términos que ocupan lugares comunes, la llamaremos ensamblaje de matrices. Nótese que las submatrices nulas que resultan en el ensamblaje del caso expuesto, tienen el significado de que los desplazamientos en el nudo 1 no generan fuerzas en el 3 y viceversa. La operación de ensamblaje no ha resuelto el problema de la singularidad de K, citado en apartados anteriores. Por la forma de proceder, resulta que al combinar las dos matrices no se ha duplicado el grado de singularidad. La matriz ensamblada sigue siendo singular de grado 3. Matriz de Rigidez completa de la estructura A efectos de generalizar el procedimiento, se expone a continuación el ensamblaje de barras en el ejemplo de referencia planteado al principio del tema.

XL YL

X

Y

12

5 4

1

2

4

3

3

1

8

9

7 14

15

13

6

11

105

11

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

−−

−−

−−−−−−

−−−−−−

−−−−

=

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

5353

4242

5353,31,323231

423242,32,2121

312131,21

uuuuuuuuuuuuuuu

FFFFFFFFFFFFFFF

Matriz de Rigidez completa de la estructura

A esta matriz de rigidez la llamamos completa ya que se refiere a todos los nudos que forman parte de la estructura. Matriz reducida. Cálculo de las incógnitas En los nudos 1, 2 y 3 son dato las fuerzas e incógnita los desplazamientos, mientras que en los nudos 4 y 5 los datos son los desplazamientos (cero en caso de empotramiento perfecto, o valores especificados si se produce, por ejemplo, un asiento en la sustentación) y las incógnitas las fuerzas (reacciones). Se puede hacer una partición en la matriz, de la forma: donde los órdenes de las submatrices son:

3x3 3x2 2x3 2x2

⎥⎦

⎤⎢⎣

⎡⎥⎦

⎤⎢⎣

⎡=⎥⎦

⎤⎢⎣

⎡

II

I

IIIIIII

IIIII

II

I

UU

KKKK

FF

,,

,,datos

incógnitas

incógnitas

datos

12

(entiéndase que son órdenes con referencia a los nudos; a su vez, cada término es una submatriz de 3x3) Desarrollando la primera fila de la expresión matricial:

FI = KI,I UI + KI,II UII De esta expresión todo es conocido salvo UI, que se puede despejar, ya que KI,I

es invertible, al no ser singular. A esta matriz KI,I la denominaremos matriz reducida de la estructura.

UI = KI,I-1 (FI -KI,II UII)

Una vez conocida UI, se puede calcular FII:

FII= KII,I UI + KI,II UII Así, ya son conocidos todos los términos de F y de U. La inversión de la matriz reducida ha sido posible gracias a que procede de suprimir algunas filas y columnas de la matriz completa, desapareciendo así la singularidad que veníamos arrastrando desde el principio. La supresión de filas y columnas se corresponde con la aplicación de ligaduras externas, que inmovilizan la estructura. Observemos que, como la singularidad era de grado 3, ésta desaparece suprimiendo al menos 3 filas y columnas; es decir, aplicando a la estructura una sustentación que sea al menos isostática. Generalización: Forma general de obtención de la matriz reducida. Condiciones de contorno (En los ejemplos que siguen, los grados de libertad se numeran: 1, 2, 3, … únicamente a efectos de simplificación. Entiéndase que su numeración sería la que les correspondiera en la numeración general de la estructura). En el ejemplo de referencia se ha supuesto empotramiento en los nudos 4 y 5. Supongamos ahora una sustentación con apoyo fijo.

Ahora f1 y f2 son incógnitas y f3 sería dato. De no existir momento aplicado en el extremo de la barra, consideraríamos f3 = 0. En cuanto a los desplazamientos, u1 = u2 = 0 (o dato) y u3 incógnita. La separación en submatrices ya no sería posible igual que en el ejemplo de referencia. Lo mismo sucedería si, en dicho ejemplo, en la numeración de los nudos no hubiéramos dejado los empotramientos en último lugar.

2

3

1

13

Tratar de buscar una numeración de g.d.l. que permita la separación en submatrices como en el ejemplo anterior, resultaría engorroso, tanto más en el caso de estructuras más complejas. Notemos que la matriz reducida no tiene por qué ser una submatriz en el sentido de partición de la matriz completa. De forma más general, puede obtenerse suprimiendo las filas y columnas que corresponden a las fuerzas incógnita y desplazamientos dato. Se obtiene la misma submatriz que resultaría de numerar los g.d.l. de la forma antes indicada, pero sin llegar a hacerlo. Para el caso del apoyo fijo, eliminaríamos las filas y columnas correspondientes a los grados de libertad 1 y 2, y mantendríamos las correspondientes al grado de libertad 3. Análogamente, para el caso de un apoyo móvil: Datos: u2 , f1 , f3 Incógnitas: u1 , u3 , f2

Eliminaríamos la fila y la columna correspondientes al g.d.l. 2.

Si son dos las barras que concurren en un apoyo, los giros en las mismas son, en general, distintos, requiriendo dos g.d.l. independientes. Datos: u1 , u2 , f3 , f4 Incógnitas: f1 , f2 , u3 , u4

Eliminaríamos la filas y las columnas correspondientes a los g.d.l. 1 y 2.

Si las dos barras están unidas rígidamente entre sí, y es el conjunto de ambas el que se une al apoyo, ambas tendrán el mismo giro. Sólo hay que considerar un g.d.l. para el giro.

En el caso de una articulación interna también son dos los g.d.l. de giro a considerar Incógnitas: u1 , u2 , u3 , u4

2

3

1

4

4

1

3

2

3

1

2

2

1

3

14

Algunos casos más:

2

1

3

4

3

2

1

5

4

3

2

1

15

Como ejemplo de lo expuesto:

Incógnitas. Tras eliminar las filas y columnas correspondientes a los desplazamientos dato (fuerzas incógnita) resulta un sistema de ecuaciones que permite determinar los desplazamientos incógnita. Finalmente, el cálculo de las fuerzas incógnita puede hacerse con:

1 2 3 4 5 6 7 8 9

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

=

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

9

8

7

6

5

4

3

2

1

9

8

7

6

5

4

3

2

1

uuuuuuuuu

fffffffff

3

1

2

5

6

4

8

9

7

16

2 3 6 9 1 4 5 7 8 UI

UD

KI,I KI,II

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢

⎣

⎡

=

⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢

⎣

⎡

8

7

5

4

1

9

6

3

2

9

6

3

2

uuuuuuuuu

ffff

donde, sub-D: datos, sub-I: incógnitas. De forma abreviada:

FD=KI,I UI + KI,II UD Nótese que la reordenación de filas y columnas, y la partición efectuadas son innecesarias. Bastaría efectuar:

F=K U con la matriz completa, aunque algunas de las fi así calculadas fueran dato. Sumandos del vector F Hasta el momento se ha supuesto implícitamente que todas las fuerzas actúan sobre los nudos de la estructura; no obstante, las fuerzas pueden actuar también a lo largo de las barras, bien como cargas puntuales o como cargas repartidas. Notemos también que la situación inicial supuesta para la estructura es con los nudos sin giros ni desplazamientos, hallando después el sistema de éstos que consigue el equilibrio de la estructura. Consideremos la barra de la figura, entre dos nudos que suponemos sin giro ni desplazamiento, sometida a unas cargas:

17

Las condiciones son las mismas de una barra biempotrada, en la que aparecen además unas reacciones de empotramiento: Llamando FL

B al sistema de fuerzas que actúan sobre uno de los extremos de la barra, en el nudo correspondiente actuará el sistema: – FL

B. Se ha puesto el subíndice L para señalar que dichas fuerzas se obtienen habitualmente en las coordenadas locales de la barra; transformadas a coordenadas globales serían FB. Por otra parte, sobre el nudo puede actuar además un sistema de fuerzas externo FN. En total, las fuerzas a considerar en el nudo serían:

F = FN - FB Los dos sumandos representan las fuerzas que llegan al nudo directamente: FN, más las fuerzas que llegan al nudo a través de la barra: -FB. Solicitaciones en los extremos de las barras Una vez obtenidos los desplazamientos en los nudos y, por tanto, en los extremos de las barras, la relación F=KU entre fuerzas y desplazamientos en los extremos de cada barra proporciona las fuerzas debidas a dichos desplazamientos en coordenadas globales, siendo K la matriz de rigidez global de la barra considerada. Para que dichas fuerzas coincidan con las solicitaciones (esfuerzo normal, esfuerzo cortante y momento flector) deben venir expresadas en coordenadas locales. Recordando que: FL=RF, y sustituyendo la expresión anterior:

FL=RKU También puede hacerse primero el cambio de los desplazamientos a coordenadas locales: UL=RU, y sustituir después en: FL = KLUL , resultando:

FL = KL R U

FLB

- FLB

18

Por supuesto, las dos expresiones obtenidas son idénticas. Recuérdese que: K = RTKLR y que: RTR = RRT = I. Veamos de forma más detallada la correspondencia entre los resultados del método matricial y las solicitaciones provocadas en los extremos de la barra por los desplazamientos de los nudos. A las solicitaciones anteriores, debidas únicamente a los desplazamientos, hemos de superponer las producidas en la situación inicial, cuando se hizo el supuesto de nudos sin desplazamiento; es decir, de barras biempotradas: FL

B. En total:

FL = KL R U + FLB

Debe prestarse especial atención al criterio de signos antes expuesto; es decir, los signos negativos del extremo primero de la barra. Numeración de nudos El orden en que se numeren los nudos tiene influencia en el tiempo de computación para la inversión de la matriz, que puede ser importante en el caso de estructuras con muchos nudos. Se define el ancho de banda de una matriz como el número de diagonales paralelas a la diagonal principal, incluida ésta, en las que no son ceros todos sus elementos. El tiempo necesario para la inversión es menor cuanto más pequeño sea el ancho de banda.

XL

YL

1

2

3

5

6

4

1 2

f1 = - Nx

f2 = - Ty

f3 = - Mz

f4 = Nx

f5 = Ty

f6 =Mz

19

Veamos en un ejemplo el ancho de banda que resulta para distintas numeraciones de nudos:

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

321 4 5 6

7 8 9 10 11 12 Numeración I

123456789

101112

1 2 3 4 5 6 7 8 9 10 11 12

Ancho de banda

20

.

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

321 4 5 6

789101112 Numeración II

123456789

101112

1 2 3 4 5 6 7 8 9 10 11 12

21

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

Como se puede apreciar, la numeración III es la mejor, ya que se obtiene un menor ancho de banda. El valor del ancho de banda para cada caso resulta:

NUMERACIÓN ANCHO DE BANDA I 8 II 12 III 3

La determinación de la numeración óptima sólo es sencilla para estructuras simples. Para estructuras más complicadas es necesario el uso de algoritmos específicos. Generalmente, los programas pueden realizar esta parte del proceso de manera que el usuario introduzca una numeración, el programa emplee la suya propia (óptima) y al final presente los resultados asociados a la numeración definida por el usuario.

3

2

1

4

5

6

7

8

9

10

11

12 Numeración III

123456789

101112

1 2 3 4 5 6 7 8 9 10 11 12

Ancho de banda

22

Método matricial para estructuras articuladas En general, en las estructuras articuladas el giro de las barras no tiene interés, lo que permite prescindir de los grados de libertad correspondientes a los giros, simplificando el procedimiento. Por lo demás, el desarrollo del método es análogo al seguido para las estructuras reticuladas. Ahora el número de grados de libertad de una barra es cuatro: De la misma manera que en las estructuras reticuladas, plantearemos: FL=KLUL, donde la nueva matriz de rigidez local es de la forma:

KL =

⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

−

−

0000

00

000

00

LEA

LEA

LEA

LEA

La matriz de rotación es:

R =

⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢

⎣

⎡

−

−−

θθθθ

θθθθ

cos00cos00

00cos00cos

sensen

sensen

Matriz de rotación R

Esta matriz se obtiene de misma la figura que ya se empleó para las estructuras reticuladas.

4

XL

YL

1

2

3

1 2

23

La relación UL=RU resulta:

⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢

⎣

⎡

⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢

⎣

⎡

−

−−=

⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢

⎣

⎡

4

3

2

1

4

3

2

1

cos00cos00

00cos00cos

uuuu

sensen

sensen

uuuu

L θθθθ

θθθθ

Los resultados a esperar serán los propios de este tipo de estructuras, es decir, las barras estarán sometidas únicamente a tracción o compresión. El vector local de fuerzas será de la forma:

FL =

⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢

⎣

⎡

0

0

3

1

F

F

Las expresiones que relacionan las coordenadas locales y globales de fuerzas y desplazamientos, así como el procedimiento de ensamblaje, la matriz reducida y el resto del método, son iguales que en las estructuras reticuladas. Efectos térmicos y errores de construcción Para la formación del vector de cargas:

F = FN-FB Y recordando la hipótesis de desplazamientos iniciales nulos en los nudos:

• Incremento de temperatura:

∆L = α L ∆T = EAFL

F = α ∆T EA Esta fuerza la introduciremos en el término FB

∆T F F

24

• Error de construcción:

EAFLL =∆ 0

LL

EAF 0∆=

Esta fuerza también la situaríamos en el término FB

Apoyo elástico

El efecto es similar al de situar un muelle en el apoyo. Por ejemplo, es una manera de representar un suelo que no pueda suponerse rígido. En el ejemplo de referencia, suponiendo apoyos elásticos según los grados de libertad 7 y 14: Se pueden seguir distintos procedimientos. Posiblemente el más sencillo consiste en añadir un nuevo nudo e interpretar el muelle como una biela. Se puede apreciar el paralelismo:

LL

EAF ∆= (biela)

ukF = (muelle)

∆L0

L

F F

F

F

25

Un muelle de constante elástica k se puede representar por una barra con valores E, A, L adecuados. La matriz de rigidez local del muelle es:

KL =

⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢

⎣

⎡

−

−

000000000000

kk

kk

La constante elástica de un terreno se puede determinar mediante un ensayo de carga, comparando el valor de P con el asiento δ producido.

δkP = ukF =

Método matricial 3D Para un caso tridimensional, el número de grados de libertad a considerar en cada nudo es 6: una traslación y una rotación sobre cada una de las direcciones X, Y, Z. Corresponden, por tanto, 12 grados de libertad en cada barra. Igual que ocurría en el caso 2D, produciendo un desplazamiento unidad sobre cada uno de los grados de libertad, a la vez que se impide el desplazamiento en los demás, se obtienen los términos de la matriz de rigidez de la barra. En la figura siguiente se esquematiza el efecto de los desplazamientos unidad.

δ

P

26

27

La matriz de rigidez de la barra es:

⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢

⎣

⎡

−

−

−

−

−−−

−

−

−

−

−−−

−

−

LIE4000

LI6E0

LIE2000

LI6E0

0L

IE40

LI6E

000L

IE20

LI6E

00

00LIG00000

LIG000

0L

I6E0

LI12E

00000L

I12E00

LI6E000

LI12E0

LI6E000

LI12E0

00000L

EA00000L

EAL

IE2000

LI6E0

LIE4

000L

I6E0

0L

IE20

LI6E

000L

IE40

LI6E

00

00LIG

00000LIG

000

0L

I6E0

LI12E

000L

I6E0

LI12E

00

LI6E000

LI12E0

LI6E000

LI12E0

00000L

EA00000L

EA

z2

zz2

z

y2

yy2

y

*0

*0

2y

3y

3y

2z

3z

2z

3z

z2

zz2

z

y2

yy2

y

*0

*0

2y

3y

2y

3y

2z

3z

2z

3z

*0I es el momento de inercia polar equivalente. En secciones circulares: 0

*0 II =

La matriz de rotación en 3D es:

R =

⎥⎥⎥⎥⎥⎥

⎦

⎤

⎢⎢⎢⎢⎢⎢

⎣

⎡

321

321

321

cosγcosγcosγ

cosβcosβcosβ

cosαcosαcosα

ZL

YL XL

XG

YG

ZG

B

A

28

Notemos que, tanto en 2D como en 3D, las expresiones de fuerzas y momentos utilizadas para el cálculo de los términos kij sólo son aplicables cuando los ejes Y-Z sobre la sección son los principales de inercia. En el ejemplo siguiente la estructura articulada representada pudiera parecer plana, pero realmente es tridimensional. Los ejes a considerar en la sección son los principales de inercia: Las articulaciones, que aparecen como dos círculos, realmente son:

XL

ZL

YL

X

Y

ZZ

X

Y

29

De acuerdo con las figuras anteriores, para considerar adecuadamente las fuerzas de ligadura, los ejes globales a considerar son:

Y

Z

X