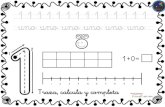
optimizacionpdf[1]

DEPARTAMENTO DE CIENCIAS-CAJAMARCA

OPTIMIZACIÓN

El objetivo de los problemas de optimización, es hallar el máximo o el mínimo absoluto

de una función.

Máximo y mínimo absoluto de una función.

Sea una función definida en un intervalo I que contiene el número c . Entonces

( )f c es el máximo absoluto de f en I si ( ) ( )f c f x para todo x en I .

( )f c es el mínimo absoluto de f en I si ( ) ( )f c f x para todo x en I .

En conjunto, los máximos y mínimos absolutos se denominan extremos absolutos

Cómo hallar los extremos absolutos de una función continua f en un intervalo

cerrado a x b

1º Hallar la coordenadas de x de todos los puntos críticos de f en el intervalo a x b

2º calcule ( )f x en estos valores críticos y en los extremos x a y x b .

3º Seleccione los valores mayor y menor de ( )f x obtenido en 2º. Estos son los

máximos y mínimos absolutos.

Ejemplo 1: Halle el máximo absoluto y el mínimo absoluto de la función 3 2( ) 2 3 12 7f x x x x , en el intervalo 3 0x

Solución:

La derivada ' 2( ) 6 6 12f x x x

6( 2)( 1)x x

Los puntos críticos son: 2, 1x x

De estos puntos solo 2x está en el intervalo 3 0x . Luego calcular ( )f x

cuando sea 2x y en los extremos del intervalo 3; 0x x .

( 3) 2f ( 2) 13f (0) 7f

Comparando los valores tenemos

( 2) 13f Máximo absoluto y

(0) 7f Mínimo absoluto


Ejemplo 2: Si tres lados de un trapecio miden cada uno 10 cm. ¿Cuánto debe medir la

base mayor para que el área sea máxima?

Solución:

La longitud de la base menor del trapecio ABCD, es 10 cm. La longitud de la base

mayor del trapecio ABCD, será 10 2x . Sea h la altura del trapecio ABCD.

En el triangulo rectángulo AMD y BNC, se cumple la relación 2 210h x

El área del trapecio será: [10 (10 2 )]

2

x hA

, luego reemplazando el valor de h :

2( ) (10 2 ) 100A x x x …………………..(1)

El área del trapecio será máxima, si y solamente si: '( ) 0A x y ' '( ) 0A x .

Derivando (1), obtenemos 2

'

2

100 10 2( )

100

x xA x

x

3' '

2 3

(1000 300 2 )( )

(100 )

x xA x

x

Hallando los puntos críticos

1. 2

'

2

100 10 2( ) 0

100

x xA x

x

2

2

2

100 10 2 0

50 5 0

5 50 0

( 10)( 5) 0

10 5

x x

x x

x x

x x

x x


2. Ver en qué puntos la derivada no existe:

2

2

100 0

100 0

(10 )(10 ) 0

10 10

x

x

x x

x x

Ahora (10) 0A

( 10) 0

(5) 75 3

A

A

Por lo tanto el área del trapecio será máxima, cuando 5x cm ; siendo el área máxima 275 3 cm .

Ejemplo 3: Se quiere hacer una caja abierta cortando pequeños cuadros congruentes en

las esquinas de una lamina de hoja que mide 12 por 12 pulgadas, y doblando los lados

hacia arriba. ¿Qué tan grandes deben ser los cuadrados que se corten de las esquinas

para que la caja tenga la máxima capacidad posible?

Solución:

El volumen de la caja será: (12 2 )(12 2 )v x x x . Como los lados de la lamina de

hojalata tienen solo 12 pulgadas de largo, 6x y el dominio de la función Volumen es

el intervalo 0 6x


Encontramos la primera derivada de la función Volumen '( ) 12(2 )(6 )V x x x

Los puntos críticos son: 6x y 6x . Luego se evalúa es la función los puntos críticos

y los extremos del intervalo.

(6) 0V

(2) 128V (Mayor)

(0) 0V

Por lo tanto el volumen será máximo cuando los cortes cuadrados deben medir 2

pulgadas por lado. El volumen máximo es 3128 lgpu .

Ejemplo 4: Dos edificios R y Q están situados a 150m y 100m respectivamente de los

puntos A y B más próximos a una línea de conducción eléctrica. Deben de conectarse

sus redes de suministro en una sub estación común P, siendo la distancia AB de 200m.

Calcular la menor longitud de cable posible que permita hacer instalación.

Solución:

Sea w la longitud del cable que se va a minimizar x x y .

Por el teorema de Pitágoras tenemos: 2 2150y x , 2 2(200 ) 100x x

2 2 2 2150 (200 ) 100w x x para 0 200x

Derivando w respecto a x

2 2 2 2

(200 )

150 (200 ) 100

dw x x

dx x x

Haciendo 0dw

dx , se obtiene:

2 2 2 2(200 ) 100 (200 ) 150x x x x

Elevando al cuadrado

2 2 2 2 2 2(200 ) 100 (200 ) 150x x x x

2 2 2 2 2 2 2(200 ) 100 (200 ) (200 ) 150x x x x x x

Desarrollando tenemos


2 720 72000 0

( 600)( 120) 0

600 120

x x

x x

x x

Pero 600 [0;200]x . Entonces

(0) 373.60w cm

(120) 320.15w cm

(200) 350w cm

Se puede concluir que la longitud mínima de cable es de 320.15cm .

Ejemplo 5: Si un lado de un campo rectangular va a tener como limite un rio, halla las

dimensiones del terreno rectangular más grande que puede cercarse usando 240m de

valla para los otros tres lados.

Solución:

Sea x el largo del lote que es paralelo al rio y sea y el ancho del lote. El área es

A xy y el perímetro es 2P x y . Veamos el dibujo:

Como el perímetro es 240m , entonces: 240 2x y , entonces 240

2

xy

.

Luego 240

2

xA xy x

21( ) 120

2A x x x

El area de la región rectangular será máxima, si y solamente si: '( ) 0A x y ' '( ) 0A x .

Veamos la primera derivada '( ) 120A x x

Puntos críticos: '( ) 0A x

120 0x

120x

El único punto crítico es 120x . La segunda derivada es: ' '( ) 1A x . Para 120x , ' '( ) 0A x , entonces se tiene un máximo.

Por lo tanto el área será máxima cuando, el largo del lote que es paralelo al rio sea

120m . El ancho del lote 240 120

602

y m

. Y el área máxima es de 27200m .


Ejemplo 6: Calcule el número de unidades x que maximiza la siguiente función de

ingresos: 2

2( )

21

xI x

x

. Y determine el valor máximo de los ingresos.

Solución:

Para determinar el máximo de la función I , calculamos en primer lugar sus puntos

críticos: 2 2

'

2 2

21 2 (2 ) 4 21( )

( 21) ( 21)

x x x x xI x

x x

' 2 2( ) 0 4 21 0 4 21 0I x x x x x

74 16 84 4 10

32 2x

Por lo tanto, la función tiene dos puntos críticos. Por no tener sentido económico,

desechamos el negativo.

Veamos si 3x , es un máximo: 2 2 2 2 3 2

''

2 4 2 3

( 2 4)( 21) 2( 21)2 ( 4 21) 2 12 126 84( )

( 21) ( 21)

x x x x x x x x xI x

x x

' ' 300 1(3) 0

27000 90I

' ' 700 1( 7) 0

343000 490I

Así pues, en 3x hay un máximo local de la función. El valor máximo de la misma es:

5 1(3)

30 6I


EJERCICIOS PROPUESTOS

1. Un fabricante de cajas de estaño desea piezas de 8 15 lgpu , cortando cuadrados

iguales en las cuatro esquinas y doblando. Calcule la longitud necesaria del lado del

cuadrado por cortar si desea que cada pieza de estaño una caja sin tapa del máximo

volumen posible.

2. El departamento de carreteras planea construir un área de excursión para

automovilistas al lado de una carretera principal. Esta área será rectangular y tendrá

5000 yardas cuadradas encerradas por un cercado en los tres lados no adyacentes a la

carretera. ¿Cuál es la cantidad mínima de cercado necesario para terminar el trabajo?

3. Durante varias semanas, el departamento de carreteras ha registrado la velocidad del

flujo de tráfico más allá de cierta salida de la ciudad. Los datos señalan que entre la 1:00

p.m. y las 6:00p.m. de un día normal de la semana, la velocidad del trafico a la salida es

de aproximadamente 3 2( ) 10.5 30 20S t t t t millas por hora, donde t es el número

de horas después del mediodía. ¿En qué instante entre la 1:00p.m. y las 6:00p.m. se

mueve más rápido el trafico y en que instante se mueve más lento ?

4. Una estación de radio que solo emite noticias realizo una encuesta sobre los hábitos

de escucha de los residentes locales entre las 5:00p.m. y la media noche. La encuesta

indica que el porcentaje de población adulta local que sintoniza la estación x después

de las 5:00p.m. es 3 21( ) ( 2 27 108 240)

8f x x x x . ¿A qué hora entre las 5:00p.m.

y la medianoche escucha la emisora el mayor número de personas?¿qué porcentaje de la

población representa los oyentes en ese momento?. ¿Y el menor número de oyentes?

5. La suma de dos números es constante. Demostrar que la suma de sus cuadrados es

minima cuando los dos números son iguales a la mitad de la suma.

6. Un granjero desea cercar un terreno rectangular, uno de cuyos lados coincide con la

orilla de un rio rectilíneo, por consiguiente, este lado no necesita cerca. El trabajo de

hechura de la cerca paralela al rio tiene un costo de $200 por cada metro lineal y para

los dos extremos es de $300 por cada metro lineal. el grajero dispone de $900000 para

efectuar la obra. Hallar las dimensiones del cercado para poder encerrar la mayor area

posible. ¿Cuál es el perímetro?

7. Una empresa tipográfica contrata la impresión de hojas sueltas que deben contener 2500cm de tema escrito con márgenes de 40cm en sus partes superior e inferior y

20cm en sus lados. Calcular las dimensiones que debe tener la hoja para emplear la

menor area de papel es decir, para lograr el costo mínimo del trabajo contratado.

8. ¿Cuál es el número tal que el cociente de su logaritmo neperiano y el número es

máximo?

9. Determinar la ecuación de la línea recta que pasa por el punto (3;4) y forma con los

ejes coordenados del primer cuadrante un triángulo de area minima.


10. Se desea construir un depósito metálico para agua, en forma de cilindro circular

recto con dos tapas. Se dispone de una lámina rectangular de superficie dada S . Sin

tener en cuenta las sobrantes de material, determinar el radio y la altura del cilindro que

permitan obtener un tanque de capacidad máxima.

11. Una ventana rectangular coronada por un semicírculo, tiene un perímetro dado.

Determinar las dimensiones que dejan pasar el máximo de luz.

12. La suma de dos números enteros es 10. Calcular los dos números, de tal manera que

la raíz cuadrada de su producto sea máxima.

13. Se tiene un triangulo escaleno, de base 12 cm. y de altura 6cm. Hallar el área del

mayor rectángulo inscrito, cuya base coincida con la base del triangulo.

14. Dada la parábola 2 16y x , calcular el área del mayor rectángulo que se puede

inscribir en la parábola, entre el vértice y su lado recto.

15. Dos edificios R y Q están situados a 150m y 100m respectivamente de los puntos

A y B más próximos a una línea de conducción eléctrica. Deben conectarse sus redes

de suministro en una sub-estación común P , siendo la distancia P de 200m . Calcular

la menor longitud de cable posible que permita hacer la instalación.

16. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo

alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el

cono engendrado de esta forma tenga volumen máximo.

17. Un depósito abierto de latón con base cuadrada y capacidad para 4 000 litros, ¿qué

dimensiones debe tener para que su fabricación sea lo más económica posible?

18. Dada la función 2( )f x x ax b . Hallar los valores de a y b , sabiendo que la

recta 5 14y x es tangente a la gráfica de f en (4;6)A .

optimizacionpdf[1]

Documents

Transcript of optimizacionpdf[1]