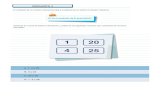
Criteriosde Diferenciacion Clinica de Kernberg Para Pregunta 4
Pregunta 4 Mate5
-
Upload
michael-castro-vasquez -
Category
Documents
-
view
216 -
download
2
description
Transcript of Pregunta 4 Mate5

Pregunta 4 Utilice el teorema de Cauchy para mostrar que las siguientes integrales son cero:
1. donde C es el círculo unitario.
Solución: Si F(z) es analítica, entonces se cumple:
Ec. De Cauchy-Riemann: ;
Entonces, Hallamos u(x,y) , v(x,y):
Donde obtenemos:
Verificamos la ecuación 1 para :

Como se puede observar, se cumple que:
Una vez que hemos comprobado que se cumplen las ecuaciones de C-R, podemos afirmar que:
Por lo tanto:
Por teorema de Cauchy-Riemann y C :
Podemos ver que el teorema de Cauchy se cumple, por lo tanto:
2. , donde C es el cuadrado con vértices: z1=1; z2=2; z3=2+i;z4=1+i.Solución:Si F (z) es una función analítica en la región R e γ una curva simple, además z0 es un polo interior, se cumple que:

Ahora verificaremos que la integral salga 0.
Observamos que z0=0, entonces:
Pero sabemos:
Entonces:

Por lo tanto, se obtiene que la función es 0.
3. , donde C es el círculo .
Solución:Si la función F(z) es analítica, entonces deben cumplir las ecuaciones de Cauchy-Riemann:
;
Hallamos u(x,y) , v(x,y):
Como en problema anterior,este es otra función demasiado grande, donde sus derivadas parciales serían aún más grandes, por lo que utilizaremos el teorema de la integral de Cauchy.
Sabemos que z0=1 ʌ C: ,
pero , entonces:

4. donde C es el círculo .
Solución:
Si la función F(z) es analítica, entonces deben cumplir las ecuaciones de Cauchy-Riemann:
;
Hallamos u(x,y) y v(x,y):
Como vemos, es una función demasiado grande, entonces utilizamos el teorema de integral de Cauchy: De la integral se obtiene que:
Y también se sabe que:
Pero:
Entonces: