Principios De Econometria - ARIMA

Principios de Econometríay modelación

Parte 10: Modelos autorregresivos

Por Lic. Gabriel Leandro, MBA

La Metodología Box – Jenkins

• El método Box-Jenkins de pronóstico es diferente de la mayoría de los métodos.

• Esta técnica no asume ningún patrón particular en los datos históricos de la serie a pronosticar. – Se utiliza un enfoque iterativo de

identificación de un modelo útil a partir de modelos de tipo general.

La Metodología Box – Jenkins

• El modelo elegido se verifica contra los datos históricos para ver si describe la serie con precisión.

• El modelo se ajusta bien si los residuos entre el modelo de pronóstico y los puntos de datos históricos son reducidos, distribuidos de manera aleatoria e independiente. – Si el modelo especificado no es satisfactorio, se

repite el proceso utilizando otro modelo diseñado para mejorar el origen.

– Este proceso se repite hasta encontrar un modelo satisfactorio.

Modelos ARIMA

• Los modelos ARIMA o modelos de promedio móvil autorregresivo integrado son un tipo general de los modelos de Box-Jenkins para series de tiempo estacionarias. – Recuerde que una serie histórica estacionaria

es aquella cuyo valor promedio no cambia a través del tiempo.

Modelos ARIMA

• Este grupo incluye a:– los modelos AR sólo con términos

autorregresivos, – los modelos MA sólo con términos de

promedio móvil y – los modelos ARIMA que comprenden tanto

términos autorregresivos como de promedio móvil.

Modelos ARIMA

• Para efectuar la selección del modelo apropiado:– Se compara la distribución de los coeficientes

de autocorrelación de la serie histórica que se está ajustando,

– con las distribuciones teóricas para los distintos modelos.

Modelos AR

• Los modelos autorregresivos se presentaron cuando se tocó el tema de las series de tiempo.

• Sin embargo, las ecuaciones que se plantearán ahora difieren en varias formas importantes.– Antes los coeficientes de regresión se estimaban

mediante el método lineal de mínimos cuadrados.– Ahora los coeficientes de regresión se encuentran por

medio de un método de mínimos cuadrados no lineal.

Modelos AR

• Por lo regular el método de mínimos cuadrados no lineal utiliza una técnica de solución iterativa para calcular los parámetros en vez de usar un cálculo directo. – Se emplean estimaciones preliminares como

puntos iniciales.– Luego estas estimaciones se mejoran

sistemáticamente hasta encontrar valores óptimos.

Modelos AR

• Además, ahora las varianzas para las ecuaciones se calculan de una forma distinta,– que toma el hecho de que las variables

independientes están relacionadas entre sí.– Por último, ahora las ecuaciones pudieran o

no contener un término constante.

Modelos AR

• La modelización ARIMA o Box-Jenkins parte de considerar que el valor observado de una serie (un dato de una variable económica) en un momento determinado de tiempo t es una realización de una variable aleatoria yt definida en dicho momento de tiempo. – Por tanto, una serie de t datos es una muestra de un

vector de t variables aleatorias ordenadas en el tiempo al que denominamos proceso estocástico.

Modelos AR

• En ocasiones pretendemos predecir el comportamiento de una variable y en un momento futuro t, a partir del comportamiento que la variable tuvo en un momento pasado, por ejemplo, en el período anterior, yt-1.– Formalmente notaríamos que

yt = f(yt-1)

– es decir, que el valor de la variable y en el momento t es función del valor tomado en el período t-1.

Modelos AR

• Puesto que en el comportamiento de una variable influyen más aspectos, debemos incluir en la relación anterior un término de error, et.– Este et es una variable aleatoria a la que

suponemos ciertas características estadísticas apropiadas.

• Es decir:

yt = f(yt-1, et)

Modelos AR

• Ahora debemos elegir una forma funcional concreta para esta expresión. – Por ejemplo, una forma lineal como

yt = 0 + 1yt-1 + et

– donde 0 es un término independiente y 1 es un parámetro que multiplica al valor de la variable y en el período t-1.

Modelos AR

• Utilizando métodos estadísticos adecuados podemos estimar los parámetros 0 y 1 de forma que estos cumplan propiedades estadísticas razonables y sean una buena (la mejor posible) estimación. – Con ello obtendríamos una expresión que

utilizaríamos a efectos de predicción.

Modelos AR

• Esta es la esencia de los modelos autorregresivos (o modelos AR).

• Se realiza una regresión de la variable yt sobre sí misma (autorregresión).– Es decir, se realiza una regresión sobre los

valores que la variable tomó en el período o periodos anteriores.

Modelos AR

• Un aspecto importante es el orden del modelo AR. – Por ejemplo, el modelo

yt = 0 + 1yt-1 + et

– es de orden 1, y se denota como AR(1).

• Si se toma en el modelo como explicativas los valores de la variable y en los 2 períodos anteriores, es decir:

yt = 0 + 1yt-1 + 2yt-2 + et

– entonces se ha especificado un AR(2).

Modelos AR

• De igual forma un AR(3) vendría dado por

yt = 0 + 1yt-1 + 2yt-2 + 3yt-3 +et

• En general, un AR(p) viene dado por

yt = 0 + 1yt-1 + 2yt-2 + …+ pyt-p +et

– Es frecuente encontrarnos con Modelos AR con un bajo orden (1 o 2).

– En series con componente estacional es habitual que el desfase sea coincidente con la periodicidad de los datos.

• En ese caso hablamos de modelos SAR.

Modelos AR en Gretl

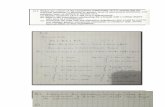
• Suponga que se tiene la siguiente serie de datos:

25, 28, 36, 34, 29, 20, 17, 21, 19, 28, 32, 25

• Y que se desea emplear un modelo AR(1) para efectuar un pronóstico de la serie.

Modelos AR en Gretl

• Primero se introduce la serie de datos.

• Es útil observar la gráfica de los datos.– Menú: Variable – Time series plot

• Para aplicar el modelo AR(1):– Menú: Model – Time series – ARIMA

• Dependent variable: Yt• AR order: 1• Difference: 0• MA order: 0

16

18

20

22

24

26

28

30

32

34

36

1950 1951 1952

Yt

Modelos AR en GretlARMA estimates using the 12 observations 1950:1-1952:4Estimated using Kalman filter (exact ML)Dependent variable: Yt

VARIABLE COEFFICIENT STDERROR T STAT P-VALUE

const 25,9867 2,69424 9,645 <0,00001 *** phi_1 0,522529 0,225317 2,319 0,02039 **

• Mean of dependent variable = 26,1667• Standard deviation of dep. var. = 6,10266

Modelos AR en Gretl

• Para efectuar pronósticos:– En la ventana del resultado del modelo:

• Menú: Analysis – Forecast• Seleccionar periodos del pronóstico

– Se obtienen dos ventanas:• Una es la del pronóstico• Otra es el gráfico

Modelos AR en Gretl

For 95% confidence intervals, z(.025) = 1,96

Obs Yt prediction std. error 95% confidence interval

1951:4 21,00 21,29 1952:1 19,00 23,38 1952:2 28,00 22,34 1952:3 32,00 27,04 1952:4 25,00 29,13 1953:1 25,47 4,839 15,99 - 34,96

14

16

18

20

22

24

26

28

30

32

34

36

1951.8 1952 1952.2 1952.4 1952.6 1952.8 1953

Ytforecast

95 percent confidence interval

Modelos SAR

• Cuando se modela una serie con estacionalidad,

• por ejemplo, la tasa de variación mensual de inflación, con 12 datos al año,

– la comparación adecuada no solo debe ser, por ejemplo, de la inflación de junio de 2004 con mayo y abril de 2004,

– sino con el mismo mes (junio) de los años anteriores, en nuestro ejemplo 2003 y 2002.

• Ello da lugar a los modelos SAR.

Modelos SAR

• La formulación sería la siguiente:– Un modelo SAR(1), también denotado como

ARs(1) viene dado por:

yt = 0 + 1yt-s + et

• donde s=4, si la serie a modelar es de frecuencia trimestral,

• o s=12, si la serie es mensual.

– Un modelo SAR(2) se especificaría como:

yt = 0 + 1yt-s + 2yt-2s + et

Modelos MA

• Una alternativa de modelización pasa por tratar de explicar el comportamiento de una variable y, no en función de los valores que tomó en el pasado (modelos AR) – sino a través de los errores al estimar el valor

de la variable en los períodos anteriores.

• Ello da lugar a los modelos de medias móviles.

Modelos MA

• Por ejemplo, un modelo MA(1) viene dado por la expresión

yt = + et + 1et-1

– donde es el valor constante alrededor del cual se mueve la variable, y ha de ser estimado igualmente con los coeficientes .

Modelos MA en Gretl

• Se introducen los datos.– Menú: Model – Time series – ARIMA– MA order: 1

Modelos MA en GretlARMA estimates using the 12 observations 1950:1-1952:4Estimated using Kalman filter (exact ML)Dependent variable: Yt


const 26,1191 2,13224 12,250 <0,00001 *** theta_1 1,00000 0,266606 3,751 0,00018 ***


Modelos MA

• En general un modelo MA(q) viene dado por la expresión:

yt = + et + 1et-1 + …+ qet-q

– Al igual que ocurría con los modelos AR, en series con componente estacional es frecuente que el retardo coincida con la periodicidad de los datos.

Modelos SMA

• En series con componente estacional (periodicidad inferior a la anual) es frecuente que en los modelos MA los retardos se establezcan no con los períodos inmediatamente anteriores, – sino que sean coincidentes con la

periodicidad de los datos.

Modelos SMA

• Así, un modelo SMA(1),o MAs(1) vendría dado por:

yt = + et + 1et-s

– donde s=4, si la serie a modelar es de frecuencia trimestral, o s=12, si la serie es mensual.

• Un modelo SMA(2) se especificaría como:

yt = + et + 1et-s + 2et-2s

Modelos ARMA

• Entre los modelos AR y los Modelos MA existe una relación que, bajo ciertas condiciones, es útil conocer.

• Los modelos ARMA integran a los modelos AR y a los modelos MA en una única expresión. – Por tanto, la variable y queda explicada en

función de los valores tomados por la variable en períodos anteriores y los errores cometidos en la estimación.

Modelos ARMA

• Una expresión general de un modelo ARMA (p, q) viene dada poryt = + 1yt-1 + …+ pyt-p + et + 1et-1 + …+ qet-q

– que, es la unión de un modelo AR(p) y un modelo MA(q).

– Obviamente, los modelos AR(p) se corresponden con modelo ARMA(p,0),

– mientras que los modelos MA(q) se corresponden con ARMA(0,q).

Modelos ARIMA

• Para la obtención de estimaciones con propiedades estadísticas adecuadas de los parámetros de un modelo ARMA, es necesario que la serie muestral que utilizamos para la estimación sea estacionaria en media y varianza.

• En un sentido laxo del término diríamos que precisamos que la serie:– no tenga tendencia, y – que presente un grado de dispersión similar en

cualquier momento de tiempo.

Modelos ARIMA

• A efectos prácticos, el cumplimiento de esta propiedad pasa por tomar logaritmos y diferenciar adecuadamente la serie original objeto de estudio.

• Con la serie ya tratada para convertirla en estacionaria ya es posible estimar un Modelo ARMA.

Modelos ARIMA

• Un Modelo Autorregresivo-Integrado de Medias Móviles de orden p, d, q – abreviadamente ARIMA(p,d,q),

• no es más que un modelo ARMA (p,q) aplicado a una serie integrada de orden d,– es decir, una serie a la que ha sido necesario

diferenciar d veces para eliminar la tendencia.

Modelos ARIMA

• Por lo tanto, la expresión general de un modelo ARIMA(p,d,q) viene dada por

dyt = 1dyt-1 + …+ pdyt-p + et + 1et-1 + …+ qet-q

– donde dyt , expresa que sobre la serie original yt, se han aplicado d diferencias.

Modelos ARIMA

• Por lo tanto, sobre una serie integrada de orden 2, necesitaría una doble diferenciación, lo cual se expresa como:

2yt = (yt) = (yt - yt-1) - (yt-1 - yt-2)

– Observe que en la expresión del ARIMA(p.d.q) desaparece el término

independiente, justamente por la aplicación de las diferencias sucesivas.

Modelos ARIMA

• Cuando la estimación del modelo ARMA se haya realizado con una serie diferenciada, a efectos de predicción, es necesario recalcularla integrando nuevamente la serie.– Por ejemplo, si mediante un modelo ARMA

(1,1) se obtuviera unos valores de predicción yt, se obtendrá la predicción final mediante:

yt = yt-1 + yt

Modelos ARIMA

• En la estimación de los modelos ARIMA el problema principal parte de identificar el modelo que mejor describe el fenómeno (la serie económica) a predecir

• Esto es, la clave de una buena predicción pasa por determinar el más adecuado de los órdenes del autorregresivo, de la media móvil, y el orden de integrabilidad.

Modelos ARIMA

• Para la determinación del orden de integrabilidad, – esto es, para determinar el número de veces

que será necesario diferenciar la serie para hacerla estacionaria en media,

– existen dos procedimientos fundamentales de detección del número de raíces unitarias,

• aparte de la simple representación gráfica, que no es más que un método intuitivo.

Modelos ARIMA

• Estos métodos para determinar el orden de integrabilidad son:– Test Dickey-Fuller o Test Dickey-Fuller

Aumentado (abreviadamente DF o ADF respectivamente) y

– el Test de Phillips-Perron (Test PP).

Modelos ARIMA

• Para la obtención del orden (p,q) se realiza una comparación entre:

1. las características que dos importantes funciones estadísticas presentan para los distintos modelos ARIMA teóricos y

2. las características que tales funciones, presentan en la serie objeto de estudio pero a nivel muestral.

Modelos ARIMA

• Tales funciones estadísticas son:– la función de autocorrelación (fac), y– la función de autocorrelación parcial (facp).

• Estas son los dos instrumentos básicos en la fase de identificación del ARIMA, al permitirnos inferir el verdadero mecanismo subyacente que han generado los datos.

Modelos ARIMA

• La fac y la facp estimadas para nuestra serie siempre se alejarán de cualquiera de las funciones de los modelos teóricos. – La clave está en la mayor aproximación de

nuestra serie a uno u otro modelo.

• Una vez identificado el modelo que subyace a nuestra serie, ya es posible la estimación de los parámetros del modelo.

Autocorrelaciones parciales

• Al principio, el analista pudiera no darse cuenta del orden apropiado del proceso autorregresivo para ajustarlo a una serie histórica. – A este mismo tipo de problema se enfrentó al

decidir el número de variables independientes a incluir en un modelo de regresión múltiple.

Autocorrelaciones parciales

• Las autocorrelaciones parciales se emplean para ayudar a identificar el grado de relación entre los valores reales de una variable y valores anteriores de la misma.– Esto mientras que se mantienen constantes

los efectos de las otras variables (períodos retrasados).

Distribuciones teóricas de los coeficientes de autocorrelación y autocorrelación parcial para algunos de

los modelos ARIMA más comunes

• Las figuras siguientes muestran las ecuaciones de un modelo AR(1), AR(2), MA(1), MA(2) y ARIMA(1,1).

• Se ilustra el comportamiento de las funciones teóricas de autocorrelación y autocorrelación parcial para estos modelos.



-1

1

0 k

-1

1

0 k

AR(1): yt = 0 + 1yt-1 + et

Autocorrelación Autocorrelación parcial



-1

1

0 k

-1

1

0 k

AR(2): yt = 0 + 1yt-1 + 2yt-2 + et




-1

1

0 k

-1

1

0 k

MA(1): yt = W0 + et - W1et-1




-1

1

0 k

-1

1

0 k

MA(2): yt = W0 + et - W1et-1 – W2et-2




-1

1

0 k

-1

1

0 k

ARIMA(1,1): yt = 0 + 1yt-1 + et - W1et-1




FAC FAP

MA(q)Se anula para retardos superiores a q

Decrecimiento rápido sin llegar a anularse

AR(p)Decrecimiento rápido sin llegar a anularse

Se anula para retardos superiores a p

ARMA(p,q) Decrecimiento rápido sin llegar a anularse

Decrecimiento rápido sin llegar a anularse



• Al seleccionar un modelo, recuerde que las distribuciones que se muestran son teóricas y que es muy improbable que las autocorrelaciones de datos reales sean exactamente idénticas a cualquiera de las distribuciones teóricas. – Se debe, mediante prueba y error, poder

ubicar en forma adecuada.

Modelos ARIMA en Gretl

• Considere la serie:

25, 28, 36, 34, 29, 20, 17, 21, 19, 28, 32, 25

• Construya un correlograma y determine cuál modelo ARIMA puede ser más apropiado.

Modelos ARIMA en GretlAutocorrelation function for Yt

LAG ACF PACF Q-stat. [p-value]

1 0,5597 * 0,5597 * 4,7850 [0,029] 2 0,0015 -0,4541 4,7851 [0,091] 3 -0,3550 -0,1871 7,1370 [0,068] 4 -0,5475 * -0,3489 13,4311 [0,009] 5 -0,3335 0,1742 16,1010 [0,007] 6 -0,0761 16,2631 [0,012] 7 0,1301 16,8320 [0,019] 8 0,1463 17,7312 [0,023] 9 -0,0071 17,7341 [0,038] 10 -0,0218 17,7741 [0,059] 11 0,0033 17,7760 [0,087]

-1

-0.5

0

0.5

1

0 2 4 6 8 10 12

lag

ACF for Yt

+- 1,96/T^0,5

-1

-0.5

0

0.5

1

0 1 2 3 4 5 6

lag

PACF for Yt

+- 1,96/T^0,5


-1

1

0 k

-1

1

0 k

ARIMA(1,1): yt = 0 + 1yt-1 + et - W1et-1



• Un modelo ARIMA(1,1) parece ser más adecuado que un modelo AR(1), AR(2), MA(1) o MA(2).

• A continuación se muestra el resultado de un modelo ARIMA(1,0,1).

Modelos ARIMA en GretlARMA estimates using the 12 observations 1950:1-1952:4Estimated using Kalman filter (exact ML)Dependent variable: Yt


const 26,1094 2,30529 11,326 <0,00001 *** phi_1 0,0926461 0,285451 0,325 0,74551 theta_1 0,999998 0,297745 3,359 0,00078 ***


Estacionalidad y Modelos ARIMA

• Los modelos ARIMA adquieren su mayor protagonismo en la predicción a corto plazo de series de frecuencia inferior a la anual (trimestral, mensual o incluso diaria).

• Por ello el tratamiento de la estacionalidad tiene un papel central en la metodología.


• En series con estacionalidad no sólo hay que modelar la componente regular (o no estacional) sino también la componente estacional.– En esos casos, lo normal es manejar un

modelo producto de dos:

ARIMA(p,d,q)*SARIMA(P,D,Q)• Donde la primera parte corresponde a la

parte regular, y la segunda a la estacional.


• A efectos de identificación del modelo estacional, se debe tener presente que la componente estacional también puede presentar una tendencia.

• Por ello, tal componente puede precisar de una o varias diferencias de orden estacional.


• Por ejemplo, para datos mensuales:12yt = (1 - B12)yt = yt - yt-12

12²yt = (1 - B12)²yt = (yt - yt-12) - (yt-12 - yt-24)


• En series con estacionalidad la identificación adquiere matices. – Junto a la identificación del orden del autorregresivo y

de la media móvil de la componente regular (ya comentado) se debe identificar los órdenes de la componente estacional.

– Para ello las reglas de identificación son similares a las comentadas para la parte estacional, pero adaptadas a la frecuencia de la serie.

• Es decir, en una serie mensual, se presta atención a los valores de las funciones para los retardos 12, 24, 36,...

• En una serie trimestral se fija la atención para los retardos 4, 8, 12,...

Fases de aplicación de la metodología ARIMA

• Aunque la identificación es la etapa sobre la que pivota toda la metodología ARIMA, lo cierto es que la aplicación de estos modelos necesita abordar un conjunto de fases entre las que existe un proceso continuo de mejora.

• Algunos detalles de estas fases ya se han ido analizando.


• Se pueden sintetizar las etapas de una aplicación ARIMA en las siguientes:1. Recogida de datos.

2. Representación gráfica.

3. Transformación previa.

4. Eliminación de tendencia.

5. Identificación del modelo.


6. Estimación de coeficientes.

7. Contraste de validez.

8. Análisis de errores.

9. Selección del modelo.

10. Predicción.

Ejercicio

• La tabla muestra los 55 promedios de cierre diario de un índice bursátil.

• Analice el comportamiento de los datos a través de la metodología expuesta en esta presentación.

n PCierre n PCierre n PCierre n PCierre

1 222,34 15 223,07 29 246,74 43 249,8

2 222,24 16 225,36 30 248,73 44 251,7

3 221,17 17 227,6 31 248,83 45 253,4

4 218,88 18 226,82 32 248,78 46 252

5 220,05 19 229,69 33 249,61 47 248,8

6 219,61 20 229,3 34 249,9 48 247,8

7 216,4 21 228,96 35 246,45 49 249,3

8 217,33 22 229,99 36 247,57 50 248

9 219,69 23 233,05 37 247,76 51 251,4

10 219,32 24 235 38 247,81 52 254,7

11 218,25 25 236,17 39 250,68 53 258,6

12 220,3 26 238,31 40 251,8 54 259,3

13 222,54 27 241,14 41 251,07 55 261,5

14 223,56 28 241,48 42 248,05

Solución

• El análisis puede iniciar observando el comportamiento de la serie a través de una gráfica.

• En Gretl:– Abrir datos.– Seleccionar PCierre– Variable – Time series plot

215

220

225

230

235

240

245

250

255

260

265

0 10 20 30 40 50

PC

ierr

e

Solución

• La gráfica parece mostrar una cierta tendencia en los datos.

• El primer paso para identificar un modelo tentativo es observar los coeficientes de autocorrelación de los datos.

• En Gretl:– Seleccionar PCierre– Variable – Correlogram – Maximum lag: 24

Autocorrelation function for PCierre

LAG ACF PACF Q-stat. [p-value]

1 0,9505 *** 0,9505 *** 52,4554 [0,000] 2 0,8999 *** -0,0376 100,3587 [0,000] 3 0,8471 *** -0,0488 143,6242 [0,000] 4 0,7954 *** -0,0171 182,5157 [0,000] 5 0,7480 *** 0,0159 217,5930 [0,000] 6 0,7075 *** 0,0441 249,6182 [0,000] 7 0,6582 *** -0,1194 277,9149 [0,000] 8 0,6092 *** -0,0269 302,6734 [0,000] 9 0,5608 *** -0,0178 324,1034 [0,000] 10 0,5051 *** -0,1020 341,8805 [0,000] 11 0,4405 *** -0,1350 355,7054 [0,000] 12 0,3810 *** 0,0028 366,2879 [0,000] 13 0,3275 ** 0,0346 374,2958 [0,000] 14 0,2773 ** -0,0178 380,1772 [0,000] 15 0,2150 -0,1968 383,8016 [0,000] 16 0,1515 -0,0612 385,6470 [0,000] 17 0,0931 0,0459 386,3626 [0,000] 18 0,0388 -0,0096 386,4900 [0,000] 19 -0,0083 -0,0025 386,4959 [0,000] 20 -0,0531 -0,0389 386,7486 [0,000] 21 -0,0966 0,0037 387,6090 [0,000] 22 -0,1470 -0,1314 389,6631 [0,000] 23 -0,1930 -0,0355 393,3107 [0,000] 24 -0,2333 * 0,0417 398,8153 [0,000]

-1

-0.5

0

0.5

1

0 5 10 15 20 25

lag

ACF for PCierre

+- 1,96/T^0,5

-1

-0.5

0

0.5

1

0 5 10 15 20 25

lag

PACF for PCierre

+- 1,96/T^0,5

Solución

• Al observarse que las primeras 12 autocorrelaciones parecen descender a cero, entonces podría decirse que la apreciación inicial de que existe tendencia era correcta.

• Para resolver este problema puede diferenciarse la serie.

Solución

• En Gretl:• Seleccionar PCierre• Add – First differences of selected variables

– Después graficar:• Seleccionar PCierre• Variable – Time series plot

– Analizar autocorrelograma:• Seleccionar PCierre• Variable – Correlogram – Maximum lag: 24

-4

-3

-2

-1

0

1

2

3

4

5

6

0 10 20 30 40 50

d_P

Cie

rre

• Autocorrelation function for d_PCierre

• LAG ACF PACF Q-stat. [p-value]

• 1 0,1853 0,1853 1,9594 [0,162]• 2 -0,0437 -0,0809 2,0707 [0,355]• 3 0,0927 0,1214 2,5801 [0,461]• 4 0,1358 0,0944 3,6955 [0,449]• 5 -0,1099 -0,1506 4,4408 [0,488]• 6 -0,0945 -0,0382 5,0036 [0,543]• 7 0,1102 0,1081 5,7846 [0,565]• 8 -0,0877 -0,1477 6,2898 [0,615]• 9 -0,1959 -0,1045 8,8690 [0,449]• 10 0,0690 0,1251 9,1961 [0,514]• 11 -0,0422 -0,1495 9,3214 [0,592]• 12 -0,0444 0,0797 9,4633 [0,663]• 13 -0,0093 0,0095 9,4698 [0,737]• 14 0,0948 0,0064 10,1493 [0,751]• 15 0,0246 0,0538 10,1961 [0,807]• 16 -0,0857 -0,0823 10,7810 [0,823]• 17 -0,0558 -0,1180 11,0359 [0,855]• 18 -0,2678 ** -0,2786 ** 17,0604 [0,519]• 19 -0,2473 * -0,1496 22,3434 [0,268]• 20 -0,0860 -0,0536 23,0019 [0,289]• 21 -0,0961 -0,0718 23,8475 [0,301]• 22 -0,0782 0,0047 24,4252 [0,325]• 23 -0,1513 -0,1472 26,6587 [0,271]• 24 0,0606 0,0616 27,0283 [0,303]

-1

-0.5

0

0.5

1

0 5 10 15 20 25

lag

ACF for d_PCierre

+- 1,96/T^0,5

-1

-0.5

0

0.5

1

0 5 10 15 20 25

lag

PACF for d_PCierre

+- 1,96/T^0,5

Solución

• La gráfica de las autocorrelaciones de los datos diferenciados muestra que los datos son estacionarios.

• En consecuencia se puede aplicar la metodología Box – Jenkins para modelar los datos.

SoluciónARIMA estimates using the 11 observations 1950:2-1952:4Estimated using Kalman filter (exact ML)Dependent variable: (1-L) Yt


const 8,31905 0,942006 8,831 <0,00001 *** phi_1 -0,387307 0,342364 -1,131 0,25794 theta_1 1,00000 0,572451 1,747 0,08066 *


Principios De Econometria - ARIMA

Travel

Transcript of Principios De Econometria - ARIMA