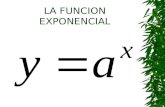DISTRIBUCION EN LA PROBABILIDAD: VARIABLE ALEATORIA DISCRETA:MULTINOMIALEn general, si un ensayo dado puede tener como consecuencia cualquiera de los k resultados posibles E1, E2, ... , Ek con probabilidades p1, p2,... , pk, la distribucin multinomial dar la probabilidad de que E1 ocurra x1veces,E2 ocurra x2 veces... y Ek ocurra xk veces en n ensayos independientes, dondex1+x2+ +xk=n.Denotaremos esta distribucin de probabilidad conjunta comof (x1, x2, ..., xk; p1, p2,... , pk,n) .Salta a la vista que p1+p2+ +pk=1, pues el resultado de cada ensayo debe ser uno de los k resultados posibles. Para derivar la frmula general procedemos como en el caso binomial. Puesto que los ensayos son independientes, cualquier orden especificado que produzca x1 resultados para E1, x2 para E2,, xk para Ek ocurrir con probabilidad. El n!mero total de ordenamientos que producen resultados similares para los nensayos es igual al n!mero de particiones den art"culos en k grupos conx1en el primer grupo, x2 en el segundo grupo,..., y xk en el ksimo grupo. Esto se puede #acer en nx1, x2, , xk=n!x1! x2! xk!formas. $omo todas las particiones son mutuamente e%cluyentes y tienen la misma probabilidad de ocurrir, obtenemos la distribucin multinomial multiplicando la probabilidad para un orden espec"fico por el n!mero total de particiones.Si un ensayo dado puede producir los k resultados E1, E2, ... , Ek con probabilidades P1, P2, , Pk, entonces la distribucin de probabilidad de las variables aleatorias x1, x2, ... , xk, que representa el n!mero de ocurrencias para E1, E2, ... , Ek en n ensayos independientes, es x(1, x2,... , xk; P1, P2, , Pk,n)=(nx1, x2, ... , xk) P1, P2, , PkX1& indica que el suceso '( aparezca %( veces )en el ejemplo, que el partido P*P* lo #ayan votado + personas,n& indica el n!mero de veces que se #a repetido el suceso )en el ejemplo, - veces,n!& es factorial de n )en el ejemplo& - . / . + . 0 . (,p1& es la probabilidad del suceso X 1 $oni=1kxi=n1i=1kpi=1.2a distribucin multinomial deriva su nombre del #ec#o de que los t3rminos de la e%pansin multinomial de )P1+P2++Pk,n corresponden a todos los posibles valores de x(1, x2,... , xk; P1, P2, , Pk,n).f EJEMPLO #14 las elecciones se presentaron / partidos pol"ticos& el P*P* obtuvo un /56 delos votos, el 7E7E el +56, el 8989 el 056 y el 2424 el (56 restante. :$ul esla probabilidad de que al elegir - ciudadanos al azar, + #ayan votado al P*P*, ( al 8989 y ( al 2424;x(1, x2,... , xk; P1, P2, , Pk,n)=n!x1! x2! xk! P1, P2, , PkEJEMPLO #2En una fiesta, el 056 de los asistentes son espa