Bases matemáticas y físicas para el estudio del movimiento

Bases matemáticas !  La media

!  Unidades de medida

!  Factores de conversión

!  Notación científica

!  Errores

!  Funciones trigonométricas

!  Magnitudes escalares y vectoriales

!  Representación geométrica de las magnitudes

!  Análisis vectorial

La medida

La medida se puede considerar como los atributos que se le asignan a las personas, las cosas o el efecto que ellas producen y que nos permite explicar los hechos de una forma precisa. !

Técnicas instrumentales

ADQUISICIÓN DE LA MEDIDA

Externas al sistema

Directas Indirectas

Internas al sistema

Unidades de medida

La medida de toda magnitud física exige compararla con cierto valor unitario de la misma.

Sistema internacional de unidades (SI): en éste sistema hay siete magnitudes fundamentales:

Magnitud Unidad (SI) Longitud Metros (m)

Masa Kilogramos (kg) Tiempo Segundos (s)

Intensidad eléctrica Ampere (A) Temperatura Kelvin (K)

Cantidad de sustancia mol Intensidad luminosa candela (cd)

Notación científica

El manejo de números muy grandes o muy pequeños se simplifica utilizando notación científica.

Ejemplos

12000000=1,2x107

15000000000=1,5x1010

0,1=10-1

0,00001=10-5

0,00003=3x10-5

Errores

"   Cifras significativas

"   Medidas experimentales

"   Tipos de errores

"   Expresión de resultados y errores

Cifras significativas Recibe el nombre de cifras significativas todo dígito (exceptuando el cero cuando se utiliza para situar el punto decimal) cuyo valor se conoce con seguridad. Ejemplos:

Número Cifras significativas 2,50 3

2,503 4 0,00103 3

Cifras significativas "   El número de cifras significativas del resultado de una

multiplicación o división no debe ser mayor que el menor número de cifras significativas de cualesquiera de los factores.

"   El resultado de la suma o resta de dos números carece

de cifras significativas más allá de la última cifra decimal en que ambos números originales tienen cifras significativas.

"   Ejemplo: 1,21342-1,040 = 0,173

Ejemplo: A=!r2; r=8 m

A=201,0619198 m2 X solo se conoce 1 cifra significativas para el radio,

por lo que A=200 m2 !

Medidas experimentales

Objetivo de la Física:

Hallar relaciones entre magnitudes físicas

¿ Qué tipos de errores hay?

¿ Cómo afectan al resultado?

¿ Cómo se expresa el resultado?

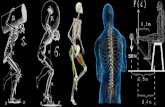
TABLA 1 TABLA 2

T (ºC) d (g/cm3) T (ºC) d (g/cm3)

40 0,8015 40 0,80

30 0,8017 30 0,80

20 0,8019 20 0,80

10 0,8021 10 0,80

Ejemplo: ¿cómo interpretar los datos?

Es importante el número de cifras al que le demos significado y es necesario algún indicador que nos garantice la fiabilidad de los resultados.

Tipos de errores

•  Errores sistemáticos Aparato de medida / Observador

SE PUEDEN ELIMINAR (aunque son difíciles de detectar)

•  Errores accidentales Condiciones experimentales / Objeto medido

SE PUEDEN REDUCIR PERO NUNCA ELIMINAR

(se pueden estimar con métodos estadísticos)

Características de las medidas

Exactitud

Cercanía al valor “exacto”

Sensibilidad Depende del

dispositivo de medida Precisión

Depende del

método experimental

Error sistemático

Error absoluto

Error relativo

Error absoluto (Ea):

estimación del error de la medida “V” (V: valor “verdadero” de la magnitud física)

V ± Ea (unidades)

Error relativo (Er):

arEEV

= ar

EE (%) 100V

=

MEDIA ARITMÉTICA V =V

i

ni=1

n

!

DESVIACIÓN MEDIA " =V

i# V

ni=1

n

!

ERROR ABSOLUTO Ea= máx S,"$% &'

Resultado final = magnitud ± error unidades

aV V E= ± unidades

Dada una medida física (V), tomamos n medidas y determinamos:

Errores en medidas indirectas

Reglas para las 4 operaciones aritméticas:

A B

A B A B

A B A B

A BA /B 2

A E ;B EE E EE B E A E

B E A EEB

±

!

± ±= += ! + !

! + !=

Ez =dzdxEx

Convención:

•  El error absoluto debe tener, en general, una cifra significativa.

•  EXCEPCIÓN: El error absoluto sólo puede darse con dos

cifras significativas si la primera de ellas es un 1, o en casos extremos, si siendo un 2, la segunda no llega a 5. En todos los otros casos debe darse un valor con una sola cifra significativa, aumentándose en una unidad si la segunda es " 5.

•  Además el valor de la magnitud debe tener sólo las cifras

necesarias para que la última cifra significativas sea del mismo orden que la ultima del error absoluto “cifra de acotamiento del valor”.

¿ Cuántas cifras significativas? En los resultados:

Hasta la 1ª cifra afectada por el error Valores incorrectos:

2.183 0.2215.412 0.07646.348 1.142248.163 0.291543 31572.35 0.045

±±±±

±±

8

3 2 0 0

Valores correctos:

2.18 0.225.41 0.0846.3 1.1248.2 0.31540 30572.35 0.05

±±±±±

±5

Funciones trigonométricas

2! = 360º 1 revolución (1 vuelta a la circunferencia)

sen! = ac= cateto opuesto

hipotenusa

cos! = bc= cateto adyacente

hipotenusa

tg! = ab= cateto opuesto

cateto adyacente= sen!

cos!

cosec! = ca= 1

sen! cot! = b

a= 1

tg!= cos!

sen! sec! = c

b= 1

cos!

!"

x

y

Circunferencia trigonométrica, radio=1

!

Magnitudes escalares y vectoriales Magnitudes escalares: quedan totalmente determinadas dando un sólo número real y una unidad de medida. Ejemplos de este tipo de magnitud son la longitud de un hilo, la masa de un cuerpo o el tiempo transcurrido entre dos sucesos. Magnitudes vectoriales: no se las puede determinar completamente mediante un número real y una unidad de medida. Por ejemplo, para dar la velocidad de un móvil en un punto del espacio, además de su intensidad se debe indicar la dirección del movimiento (dada por la recta tangente a la trayectoria en cada punto) y el sentido de movimiento en esa dirección (dado por las dos posibles orientaciones de la recta).

El valor concreto de una magnitud vectorial debe representarse mediante un vector o segmento que tiene una orientación concreta en el espacio y su origen coincide con su punto de aplicación.

a)  Su punto de aplicación, representado por O, coincide con el origen del vector.

b)  Su longitud, el módulo o magnitud escalar |a|.

c)  La recta sobre la que se halla situado el vector, la cual define la dirección.

d)  La flecha indica el sentido de aplicación en un espacio vectorial (R2)

Elementos de una magnitud vectorial:

a!

O

X

Y

Representación geométrica de las magnitudes

Representación geométrica unidimensional de un escalar

Representación geométrica bidimensional de un vector

a!= (ax,ay )

X

Y

ax

ay

a!

O

Para representar correctamente un vector es necesario:

a) Dos rectas perpendiculares entre sí, (X y Y).

b) Un punto O de intersección de las rectas que define el origen de coordenadas.

c) u1 y u2 son los vectores unitarios. u1=(1,0) y u2=(0,1).

Elementos que componen la r e p r e s e n t a c i ó n e n u n espacio bidimensional

Def

inir

un s

iste

ma

de c

oord

enad

as

X

Y

ax

ay a!

O u!x

u!y{

Vector unitario: Se define como un vector cuyo módulo es la unidad y tanto su dirección como su sentido son los del vector del que es unitario.

u!"a =

a!

a

De donde se deduce que el vector unitario puede expresarse como:

Representación gráfica de un vector con respecto a sus vectores unitarios

a!= u!"a + u!"a + u!"a + u!"a + u!"a = 5u!"a = a .u

!"a

a!

u!a

Las componentes ax y ay son perpendiculares entre sí y forman con el vector un triángulo rectángulo. Entonces se puede utilizar el Teorema de Pitágoras para calcular el módulo del vector a:

Componentes rectangulares que definen un vector

a = a x2+ a y

2

Módulo de a a!= (ax,ay )

X

Y

ax

ay

a!

O

En el espacio (R3)

a!= a x

2+ a y2+ a z

2

Representación geométrica de un vector en el espacio tridimensional

a!

Cosenos directores En una base ortonormal, se llaman cosenos directores del vector a = (x, y, z), a los cosenos de los ángulos que forma el vector con los vectores de la base.

cos! = x

x2 + y2 + z2

cos" = y

x2 + y2 + z2

cos# = z

x2 + y2 + z2

a!

Análisis vectorial "   Suma de vectores

Representación geométrica de la suma de vectores

X

Y

c!= a!+ b!

= (ax + bx )x + (ay + by )y

Problema 1

Se muestra la trayectoria de un balo después de haber sido golpeado. Calcula el desplazamiento resultante.

X

Y

Z

Ejemplo

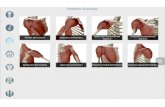
Representación gráfica de las fuerzas (músculos) que actúan sobre la rótula

Vasto externo

Vasto interno Recto femoral

Fibras largas del VI

Fibras oblicuas del VI

"   Producto de un número por un vector

! = 3

X

Z

Y

"   Producto escalar o producto punto de dos vectores Viene definido por la siguiente operación:

De donde se puede determinar el ángulo entre los vectores:

a !b = a b cos!

a !b = a1b1+a2b2+a3b3

cos! =a1b1+a2b2+a3b3

a b

El resultado es un escalar!

Interpretación: El valor absoluto del producto escalar de dos vectores no nulos es igual al módulo de uno de ellos por la proyección del otro sobre él.

bcos!!

Problema 2

Se definen los vectores de posición en el espacio del brazo a y antebrazo b: a=(0.2-0.3),(0.5-1),(2-1.6)=(-0.1,-0.5,0.4) b=(0.3-0.3),(0.8-1),(1-1.6)=(0,-0.2,-0.6)

Calcular el ángulo formado por dos segmentos contiguos que están unidos por una articulación determinada.

X

Z

Y

"   Producto vectorial de dos vectores

El módulo del vector c se define como:

La expresión analítica del producto vectorial de los vectores a=(a1,a2,a3) y b=(b1,b2,b3), se define como el desarrollo del determinante de la matriz formada de la siguiente forma:

c = a! b = a b sen!

a! b =i j ka1 a2 a3b1 b2 b3

El resultado es un vector!

Interpretación: geométricamente, el módulo del producto vectorial de dos vectores coincide con el área del paralelogramo que tiene por la dos a esos vectores.

Problema 3 Calcula el área del paralelogramo de la figura.

Cálculo diferencial X

Cálculo integral