TEMA V: FUNCIONES › 2015 › 04 › ... · 2015-04-22 · 3 Ejemplo: f ( ) 3 3x 2 6 D(f) = R f...
16
Tema: Funciones Matemáticas B – 4ºESO 1 TEMA: FUNCIONES: ÍNDICE: 1. Introducción. 2. Dominio y recorrido. 3. Gráficas de funciones elementales. Funciones definidas a trozos. 4. Continuidad. 5. Crecimiento y decrecimiento, máximos y mínimos. 6. Concavidad y convexidad. 7. Puntos de corte con los ejes. 8. Simetría. 9. Periodicidad. 10. Asíntotas. 11. Tasa variación media 1. INTRODUCCIÓN: Puntos y coordenadas Para representar en el plano se toman dos rectas perpendiculares OX y OY, llamadas ejes de coordenadas. El eje OX se llama eje de abscisa y el eje OY eje de ordenadas . El punto O es el origen de coordenadas . Cada uno de estos ejes se gradúa con números positivos y números negativos. De este modo, a cada punto P del plano le corresponde un par de números (x, y) que llamamos coordenadas del punto. El 1 er número o 1ª coordenada “x” corresponde al eje horizontal (abscisa). El 2º número ó 2ª coordenada “y” corresponde al eje vertical (ordenada) Cuadrantes 1 er cuadrante, 0 , 0 y x 2º cuadrante, 0 , 0 y x 3 er cuadrante, 0 , 0 y x 4º cuadrante, 0 , 0 y x Ejemplo: Representar en el plano los siguientes puntos (1, 2); (-3,4); (2,-5); (-4, -3) Qué es una función: “ ) ( x f y ” Una función es una relación entre dos magnitudes, de manera que a cada valor de la primera magnitud le corresponde un único valor de la segunda, que se llama imagen. Una función puede venir dada por una fórmula, por ejemplo: la relación y = 5x 2 + 1, expresa que la variable x depende de la variable y, por eso se llama a x variable independiente, y a y variable dependiente. Variable independiente Representa los distintos valores que se admiten y constituyen el dominio de la función. Variable dependiente Representa los distintos valores que resultan a partir de los valores de x. El conjunto de los valores de y constituye el recorrido o rango de la función.
Transcript of TEMA V: FUNCIONES › 2015 › 04 › ... · 2015-04-22 · 3 Ejemplo: f ( ) 3 3x 2 6 D(f) = R f...
Tema: Funciones
Matemáticas B – 4ºESO
1
TEMA: FUNCIONES: ÍNDICE:
1. Introducción.
2. Dominio y recorrido.
3. Gráficas de funciones elementales. Funciones definidas a trozos.
4. Continuidad.
5. Crecimiento y decrecimiento, máximos y mínimos.
6. Concavidad y convexidad.
7. Puntos de corte con los ejes.
8. Simetría.
9. Periodicidad.
10. Asíntotas.
11. Tasa variación media
1. INTRODUCCIÓN:
Puntos y coordenadas
Para representar en el plano se toman dos rectas perpendiculares OX y OY, llamadas ejes de coordenadas.
El eje OX se llama eje de abscisa y el eje OY eje de ordenadas. El punto O es el origen de coordenadas.
Cada uno de estos ejes se gradúa con números positivos y números negativos. De este modo, a cada punto P
del plano le corresponde un par de números (x, y) que llamamos coordenadas del punto.
El 1er número o 1ª coordenada “x” corresponde al eje horizontal (abscisa).
El 2º número ó 2ª coordenada “y” corresponde al eje vertical (ordenada)
Cuadrantes
1er cuadrante, 0,0 yx
2º cuadrante, 0,0 yx
3er cuadrante, 0,0 yx
4º cuadrante, 0,0 yx
Ejemplo: Representar en el plano los siguientes puntos (1, 2); (-3,4); (2,-5); (-4, -3)
Qué es una función: “ )(xfy ”
Una función es una relación entre dos magnitudes, de manera que a cada valor de la primera
magnitud le corresponde un único valor de la segunda, que se llama imagen.
Una función puede venir dada por una fórmula, por ejemplo: la relación y = 5x2 + 1, expresa que la
variable x depende de la variable y, por eso se llama a x variable independiente, y a y variable
dependiente.
Variable independiente
Representa los distintos valores que se admiten y constituyen el dominio de la función.
Variable dependiente
Representa los distintos valores que resultan a partir de los valores de x. El conjunto de los
valores de y constituye el recorrido o rango de la función.
2
2. DOMINIO Y RECORRIDO:
Dominio y recorrido:
El dominio “D(f)” de una función son los valores que puede tomar la x.
El recorrido o imagen “R(f)” o “Img(f)” de una función son los valores que toma la y.
Ejemplo: Para la función dada por la fórmula x
y4
:
El dominio son todos los números reales menos el 0 porque si x = 0, 0
4y , que no
tiene sentido. Es decir D(f) = R-{0}
El recorrido son todos los números reales menos el 0, pues la ecuación x
40 no tiene
solución. Ejercicio: Indica el Dominio y el recorrido de las siguientes funciones:
Cálculo del Dominio de una función.
a. Funciones Polinómicas: D( f ) = R . Ejemplo: 7532)( 24 xxxxf
b. Funciones Racionales: }min{)( adordenoelanulasedondepuntosRfD
Ejemplo: 3
6)(
3
x
xxf }3{)( RfD
32
123)(
2
2
xx
xxf }1,3{)( RfD
c. Funciones Radicales (Raíces) :
a. Índice Impar: D(f) = Dominio del radicando
b. Índice Par: D(f) = {Puntos donde el radicando es positivo o cero}
3
Ejemplo: 3 2 63)( xxf D(f) = R
63)( 2 xxf ),2U2,()f(D
5
2
3)(
x
xxf }2{)( RfD
2
3)(
x
xxf ),2(0,()( UfD
Ejercicio: Calcular el dominio de las siguientes funciones:
a. 52
73)(
2
x
xxf
b. 978)( 23 xxxg
c. 3 2 765)( xxxh
d. 532)( 2 xxxk
e. 1)( 2 xxl
f. 1
53)(
2
x
xxi
3. GRÁFICAS DE LAS FUNCIONES ELEMENTALES A cada expresión algebraica de una función le corresponde una gráfica. Mediante la gráfica de una
función podemos apreciar las características principales de dicha función.
a. Función constante. axfy )(
Su gráfica es una línea recta que pasa por el punto (0,a) y es paralela al eje OX
b. Funciones afines y lineales:
I. Función lineal. mxxfy )(
Su gráfica es una recta que pasa por el origen de coordenadas (0,0) y tiene de pendiente m. Se
representa muy fácilmente mediante una tabla de valores.
II. Función afín. nmxxfy )(
Su gráfica es una recta que pasa por el punto (0,n) y tiene de pendiente m. Se representa muy
fácilmente mediante una tabla de valores.
c. Funciones cuadráticas: cbxaxxfy 2)(
Su gráfica es una parábola.(Veamos como representarla)
Curvatura: si 00 asiperoa
Vértice: a
bVx
2
y
a
bfVfV xy
2
Puntos de corte con los ejes:
Corte con el eje 0Y tomo x = 0 y calculo “y”
Corte con el eje 0X tomo y =0 y calculo “x” (pueden ser 0,1 ó 2 valores)
Tabla de valores
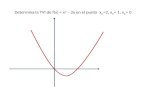
Ejemplo: 6)( 2 xxyxf
Curvatura: como a = 1 > 0 Convexa ( )
Vértice: 5̀02
1
xV y 25`6
4
25
2
1
fVy
Nota: x=2 no está en el dominio,
pues en ese punto se anula el
denominador
4
Por tanto el vértice es )25`6;5̀0()4
25;
2
1(
V
Puntos de corte con los ejes:
Eje 0Y tomo x = 0 entonces 6)0( fy el punto es (0, -6)
Eje 0X tomo y = 0 entonces 0 = 62 xx y calculo “x”
obtengo dos valores de x, x = -3 y x = 2 (-3,0) y (2,0)
Tabla de valores:
d. Funciones exponenciales.
I. 0
)(
a
axfy x
II. 0
)(
a
axfy x
III. xexfy )( ;
xexfy )( (análogo a las anteriores tomando a=e= 2´718…)
5
e. Valor Absoluto.
I. Ejemplo1: 3)( xxf
Estudio el signo de x + 3 303 xx
Por tanto
33
333)(
xsix
xsixxxf
II. Ejemplo2: 5)( 2 xxf
Estudio el signo de 55055 222 xxxx
Por tanto
55
555
55
)(
2
2
2
xsix
xsix
xsix
xf
Ejercicio: Representar las siguientes funciones:
a. 3)( xf
b. 74 xy
c. 432 xxy
d. tth 4)(
e. sesg )(
f. 143)( 2 xxxg
g. 52)( tth
h. 32)( 2 xxxf
Funciones Definidas a Trozos:
Ejercicio: Representa las siguientes funciones:
a.
35
3382
32
)( 2
xsi
xsixx
xsix
xf
b.
243
20
0
)(
2
tsit
tsit
tsit
tg
c.
112
10
12
)(
2 xsix
xsix
xsi
xh
x
d.
1)1log(
113
163
2
xsix
xsixx
xsix
xj
4. CONTINUIDAD.
Idea de continuidad en un punto:
Una función )(xfy es continua cuando puede dibujarse sin levantar el lápiz del papel.
6
Continuidad en un intervalo:
Una función f(x) es continua en un intervalo “(a, b)” cuando es continua en todos sus puntos.
a) Es continua
b) Es discontinua en el punto x=3, porque supone un salto de dos unidades en f(x). c) Es discontinua en el punto x=0 porque no está definida en el punto f (0).
Tipos de discontinuidad:
a) Discontinuidad evitable.
b) Inevitable de salto finito. (Ejemplo “b” anterior. En este caso el Salto de la función es 2)
c) Inevitable de salto infinito (Ejemplo “c” anterior)
Ejercicio: Dada la gráfica de la siguiente función:
Ejercicio. Dada las gráficas de las siguientes funciones:
Estudia:
a) Continuidad en x=3
b) Continuidad en x=0
c) Continuidad en el intervalo (-1, 0)
d) Continuidad en el intervalo (-1, 4)
e) Indica en que puntos es continua cada función.
Estudia:
a) Continuidad en el 0 b) Continuidad en el 1
c) Continuidad en el intervalo (0,2).
d) Continuidad en el intervalo (1,3)
7
5. CRECIMIENTO Y DECRECIMIENTO, MÁXIMOS Y MÍNIMOS.
Función creciente:
Una función f(x) es creciente en un intervalo si para todo par de valores hxx se verifica
que )()( hxfxf .
Si )()( hxfxfhxx
Función decreciente:
Una función f(x) es decreciente en un intervalo si para todo par de valores hxx se
verifica que )()( hxfxf .
.
Si )()( hxfxfhxx
Función constante:
Una función f(x) es constante en un intervalo si para todo par de valores hxx se verifica
que )()( hxfxf .
Si )()( hxfxfhxx
Máximo:
Una función tiene un máximo en el punto “c”, si existe un intervalo (c-h , c+h) donde se verifica
que f(c) > f(x) para todo valor “x” perteneciente al intervalo.
8
Mínimo:
Una función tiene un mínimo en el punto “c”, si existe un intervalo (c-h , c+h) donde se verifica
que f(c) < f(x) para todo valor “x” perteneciente al intervalo.
Ejemplo:
Ejercicio: Indica los intervalos de crecimiento y decrecimiento y los máximos y mínimos de las
siguientes funciones (Indicando en caso de que existan los máximos y mínimos absolutos)
6. CONCAVIDAD Y CONVEXIDAD.
Función convexa:
Una función es convexa en un intervalo si, al unir dos puntos cualesquiera del intervalo, el
segmento queda por encima de la gráfica de la función.
Función cóncava:
Una función es cóncava en un intervalo si, al unir dos puntos cualesquiera del intervalo, el
segmento queda por debajo de la gráfica de la función.
Puntos de inflexión:
Los puntos de inflexión son aquellos en los que la función cambia de curvatura.
9
Ejercicio: Indica los intervalos de crecimiento y decrecimiento, los intervalos de concavidad y
convexidad, así como los máximos, mínimos y puntos de inflexión de la siguiente gráfica:
Ejercicio: Estudia todo lo visto hasta ahora en la siguiente función:
7. PUNTOS DE CORTE CON LOS EJES.
Con el eje de abscisas (eje OX): buscamos los puntos “x” de la función )(xfy donde la
ordenada es “0” (y = 0) , luego resolvemos la ecuación 0)( xf
Con el eje de ordenadas (eje OY): buscamos los puntos “y” de la función )(xfy donde la
abscisa es “0” (x = 0), luego resolvemos la ecuación )0(fy
Ejemplo: Calcula los puntos de corte de las siguientes funciones:
a) 143)( 2 xxxf
b) 3
5)(
x
xxg
c) 1)( 2 xxxh
d) 22 21052)( xxxxi
Ejercicio: Indica en que intervalos las siguientes funciones son positivas, y en cuales son negativas:
10
a) xxf 210)(
b) 37)( xxg
c) 12)( 2 xxxh
d) 143)( 2 xxxi
e) 3)( 2 xxj
8. SIMETRÍA.
Una función es simétrica respecto del eje de ordenadas ( eje OY) cuando )()( xfxf . Se
llama también función par.
Una función es simétrica respecto del origen cuando )()( xfxf . Se llama también función
impar.
Ejercicio: Estudia la simetría de las siguientes funciones:
5
3)(;)(;
1)(;
)1(
1)(;5)(;3)(
3
2
33
2
2
43
x
xxh
xx
xxg
xx
xxf
xxhxxgxxf
9. PERIODICIDAD.
Una función es periódica cuando los valores que toma se repiten cada cierto intervalo fijo T;
que se llama periodo. Esto es, si:
)()( xfTxf
Ejemplo:
Ejemplos:
a. Funciones trigonométricas.
b. Altura de una noria en función del tiempo
c. Péndulo
d. Electrocardiograma.
10. ASÍNTOTAS.
Las asíntotas son rectas a las cuales la función se va aproximando indefinidamente sin llegar nunca a
cortarlas.
11
Asíntotas horizontales:
Ejemplo: Asíntota horizontal: y=3
Asíntotas verticales:
Ejemplo:
Asíntota vertical: x=0
Ejercicio: Estudia las asíntotas de las tres gráficas siguientes:
12
Ejercicios:
1. Indica el dominio y recorrido de las funciones:
2. Indica por qué las gráficas adjuntas no corresponden a las de una función:
3. Construye una tabla de valores asociada a cada una de las funciones:
a. A cada número le corresponde su mitad.
b. A cada cuadrado le corresponde su superficie:
4. Traza las gráficas del ejercicio anterior:
a.
5. Di si son continuas las siguientes funciones; en caso contrario, da los puntos de discontinuidad, y
el dominio:
6. Di si son continuas las siguientes funciones; en caso contrario, da los puntos de discontinuidad, y
el dominio:
7. Di si son continuas las siguientes funciones; en caso contrario, da los puntos de discontinuidad, y
el dominio:
13
8. Calcula los puntos de corte con los ejes en el ejercicio anterior:
9. Calcula los puntos de corte con los ejes en las siguientes funciones:
10. Indica entre que valores la función es creciente y entre cuáles decreciente:
11. Dibuja la gráfica de una función que sea decreciente entre 5 y 1; y entre 4 y 6, y creciente
entre 1 y 4; y entre 6 y 9.
12. Representa una función f con Dom(f)=[0,7] y R(f)=[1,5] y que, además, cumpla:
a. Crece en el intervalo (1,4) y decrece en el resto.
b. Crece en el intervalo (1,3), decrece en el intervalo (3,4) y se mantiene constante hasta
x=7.
13. Indica los intervalos de crecimiento y decrecimiento de las gráficas:
14. Indica los máximos y los mínimos de las funciones dadas en el ejercicio anterior
15. Indica los intervalos de crecimiento y decrecimiento, y los máximos y los mínimos de las
funciones dadas por las siguientes gráficas:
16. Indica los intervalos de crecimiento y decrecimiento, y los máximos y los mínimos de las
funciones dadas por las siguientes gráficas:
14
17. Indica los intervalos de concavidad y de convexidad en los ejercicios anteriores (25, 27, 28, 30,
31)
18. Dibuja una función que pase por los puntos A(1,3), B(0,1), C(2,0), D(4,3) y E(6,6), siendo A y E
máximos, C mínimo y B y D puntos de inflexión. Indica en qué intervalos es cóncava y en cuáles
convexa.
19. Completa estas gráficas para que sean simétricas:
20. Di de qué tipo de simetría presentan las siguientes funciones dadas por sus gráficas:
21. Di cuáles de las siguientes funciones son periódicas. En caso afirmativo, determina su periodo.
22. Interpreta la siguiente gráfica:
15
23. En una finca en la que se plantan dos tipos de hortalizas: tomates y lechugas, se van a utilizar “x” kilos
de abono. Las cantidades de kilos de tomates y lechugas obtenidos en función del abono utilizado vienen
dadas respectivamente por las dos funciones siguientes: 10
100300)(
x
xxT y
10
30120)(
x
xxL .
a. ¿Cuántos kilos de lechuga obtendré si uso 30 kilos de abono?
b. ¿Cuántos kilos de abono necesito para obtener 155 kilos de tomate?.
c. ¿Cuál es la función “h(x)” que nos da la cantidad de kilos de hortalizas obtenidas, en función del
abono utilizado?
d. ¿Cuántos kilos de hortalizas obtendré con 60 kilos de abono?
24. El dueño de un manantial de agua mineral llega a la conclusión de que, si el precio a que vende la botella
es “x” pesetas, sus beneficios vendrán dados por la fórmula 2110)( 2 xxxB en miles de pesetas
por día.
Representar la función precio-beneficio e indicar cuál será el precio de la botella para obtener el
beneficio máximo.
25. El día uno de mayo el precio del melón es de 200 pesetas el kilo. Cada día que pasa, el precio por kilo
disminuye en 2 ptas. Un agricultor tiene el uno de mayo 80 kilos de melones y estima producir cada día
10 kilos más. ¿Cuándo deberá vender el agricultor sus melones?
26. Algunos expertos estimaron, a comienzos de los años noventa, que el SIDA crecía a razón del 20%
anual. Si suponemos que en esa fecha, en una determinada ciudad, había 1000 enfermos de SIDA y la
fórmula del crecimiento viene dada por ttE 20,01·1000)( se pide:
a. ¿Cuántos habría a comienzos de 1993?. ¿Y en el año 2000?
b. ¿Cuánto tardará en duplicarse el número de afectados?
27. Las funciones de ingresos y costes anuales por la fabricación y venta de “q” unidades de un determinado
producto vienen dadas por: 204,02000)( qqqI y
2001,01001000000)( qqqC . Halla:
a. La función que da el beneficio anual.
b. ¿Cuántas unidades hay que producir y vender para que el beneficio sea máximo?
c. ¿Cuál es ese beneficio?
d. El coste de producción de “x” unidades diarias de un determinado producto es 2554
1 2 xx
y el precio de venta de una de ellas está en función de la producción total es
450
x euros
por cada unidad.
i. Hallar el precio de venta si se producen 12 unidades.
ii. Determinar los ingresos al producir 12 unidades.
iii. Determinar los beneficios al producir 12 unidades.
iv. Establecer la función que da los beneficios en función de las unidades vendidas.
v. Establecer el número de unidades que deben producirse diariamente para que el
beneficio sea máximo.
NOTA: BENEFICIOS = INGRESOS – GASTOS
16
