1

Hallar los elementos principales: Coordenadas

de los vértices del lado mayor y menor, las

coordenadas de los focos, los lados rectos, las

coordenadas de los extremos de los lados

rectos, las directrices, las asíntotas y las

gráficas de las siguientes ecuaciones:

𝟒𝒙𝟐 + 𝒚𝟐 − 𝟑𝒙 + 𝟒𝒚 − 𝟖 = 𝟏𝟎

2

3

4

SALIR

𝟏𝟔𝒙𝟐 + 𝟐𝟓𝒚𝟐 − 𝟒𝟖𝒙 + 𝟏𝟎𝟎𝒚 − 𝟐𝟔𝟒 = 𝟎

𝟗𝒙𝟐 + 𝟏𝟔𝒚𝟐 − 𝟏𝟒𝟒 = 0

𝟐𝟓𝒙𝟐 + 𝟏𝟔𝒚𝟐 = 𝟒𝟎𝟎

SOLUCIÓN 1

Datos del problema: 𝟗𝒙𝟐 + 𝟏𝟔𝒚𝟐 − 𝟏𝟒𝟒 =0

Dividimos ambos miembros entre el término

independiente, desarrollamos y operamos :

9𝑥2 + 16𝑦2 − 144 = 0 →9𝑥2

144+16𝑦2

144−144

144=

0

144

𝑥2

1449

+16𝑦2

14416

− 1 = 0 →𝑥2

16+𝑦2

9= 1 (𝑎)

La ecuación (a) es de la forma:𝑥2

𝑎2+

𝑦2

𝑏2= 1 ; que

representa la ecuación de una elipse horizontal

con centro C(0,0). Donde se tiene:

Semieje Mayor: 𝑎2 = 16 → 𝑎 = ±4

Semieje Menor: 𝑏2 = 9 → 𝑏 = ±3

A «c» que es la semidistancia focal lo obtenemos

con la aplicación del Teorema de Pitágoras para

elipses, es decir: 𝑎2 = 𝑏2 + 𝑐2 → 𝑐 = 𝑎2 − 𝑏2 →

𝑐 = ± 7

Luego las coordenadas de los vértices son:

El mayor es:

𝑉2 −𝑎, 0 𝑦 𝑉1 𝑎, 0 → 𝑉2 −4,0 𝑦 𝑉1 4,0

El menor es:

𝐵2 0,−𝑏 𝑦 𝐵1 0, 𝑏 → 𝐵2 0,−3 𝑦 𝐵1 0,3

IR AL MENÚ SIGUIENTE

Las coordenadas de los focos son:

𝐹2 −𝑐, 0 𝑦 𝐹1 𝑐, 0 → 𝐹2 − 7, 0 𝑦 𝐹1 7, 0

La excentricidad es: 𝑒 =𝑐

𝑎→ 𝑒 =

7

4→ 𝑒 = 0,7 < 1

El lado recto es: 𝐿𝑅 =2𝑏2

𝑎→ 𝐿𝑅 =

2(3)2

4→ 𝐿𝑅 =

9

2

Longitud del Lado mayor: 𝑉2𝑉1 = 2𝑎 → 𝑉2𝑉1 = 2 4 → 𝑉2𝑉1 = 8Longitud del Lado mayor: 𝐵2𝐵1 = 2𝑏 → 𝐵2𝐵1 = 2 3 → 𝐵2𝐵1 = 6Longitud de la distancia Focal: 𝐹2𝐹1 = 2𝑐 → 𝐹2𝐹1 = 2 7 → 𝐹2𝐹1 = 2 7

Las ecuaciones de las directrices son:

𝐷1: 𝑥1 = ℎ +

𝑎2

𝑐→ 𝐷1: 𝑥1 = 0 +

16

7→ 𝐷1: 𝑥1 =

16

7

𝐷2: 𝑥2 = ℎ −𝑎2

𝑐→ 𝐷2: 𝑥2 = 0 −

16

7→ 𝐷2: 𝑥2 = −

16

7

Los extremos de los lados rectos son:

𝐿𝑅1: 𝐿𝑅1𝐴 7,9

4𝐿𝑅1𝐵 7,−

9

4

𝐿𝑅2: 𝐿𝑅2𝐷 − 7,9

4𝐿𝑅2𝐸 − 7,−

9

4

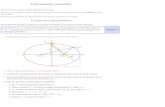
La gráfica es la siguiente:

IR AL MENUANTERIOR

SOLUCIÓN 2

Datos del

problema:

𝟐𝟓𝒙𝟐 + 𝟏𝟔𝒚𝟐 = 𝟒𝟎𝟎

𝟐𝟓𝒙𝟐 + 𝟏𝟔𝒚𝟐 = 𝟒𝟎𝟎 →𝟐𝟓𝒙𝟐

𝟒𝟎𝟎+

𝟏𝟔𝒚𝟐

𝟒𝟎𝟎=

𝟒𝟎𝟎

𝟒𝟎𝟎

𝒙𝟐

𝟏𝟔+

𝒚𝟐

𝟐𝟓= 𝟏, tiene la forma

𝒙𝟐

𝒃𝟐+

𝒚𝟐

𝒂𝟐= 𝟏, que

representa la ecuación de una elipse vertical con

centro en C(0,0).

Donde:

𝑏2 = 16 → 𝑏 = ±4; 𝑎2 = 25 → 𝑎 = ±5

El término «c» se halla mediante la relación

pitagórica, es decir: 𝑎2 = 𝑏2 + 𝑐2 → 𝑐2 = 𝑎2 − 𝑏2 =25 − 16

𝑐2 = 9 → 𝑐 = ±3

Las coordenadas de los vértices mayor y menor

son:

𝑉2 0,−𝑎 𝑦 𝑉1 0, 𝑎 → 𝑉2 0,−5 𝑦 𝑉1 0,5

𝐵2 −𝑏, 0 𝑦 𝐵1 𝑏, 0 → 𝐵2 0, −4 𝑦 𝐵1 0,4

Las coordenadas de los focos son:

𝐹2 0,−𝑐 𝑦 𝐹1 0, 𝑐 → 𝐹2 0,−3 𝑦 𝐹1 0,3

La excentricidad es 𝑒 =𝑐

𝑎→ 𝑒 =

3

5< 1

Las Directrices es:

𝐷: 𝑘 ±𝑎2

𝑐→

𝐷1: 𝑦1 = 𝑘 +𝑎2

𝑐→ 𝐷1: 𝑦1 = 0 +

25

3

𝐷2: 𝑦2 = 𝑘 −𝑎2

𝑐→ 𝐷2: 𝑦2 = 0 −

25

3

𝐷2: 𝑦1 =25

y 𝐷2: 𝑦2 = −25

SIGUIENTEIR AL MENU

La distancia del eje Mayor es:𝑉2𝑉1 = 2𝑎; 𝑉2𝑉1=10

La distancia del Eje Menor es: 𝐵2𝐵1 = 2𝑏;𝐵2𝐵1 =8

La distancia Focal es: 𝐹2𝐹1 = 2c; 𝐹2𝐹1 =6

Los lados rectos son:

Las coordenadas de los extremos del lado recto de arriba:

𝐿𝑅1𝐼𝑍𝑄(ℎ −𝑏2

𝑎, 𝑘 + 𝑐) y 𝐿𝑅1𝐷𝐸𝑅(ℎ +

𝑏2

𝑎, 𝑘 + 𝑐)

𝐿𝑅1𝐼𝑍𝑄 ℎ −𝑏2

𝑎, 𝑘 + 𝑐 → 𝐿𝑅1𝐼𝑍𝑄(0 −

4 2

5, 0 + 3)

𝑳𝑹𝟏𝑰𝒁𝑸(−𝟏𝟔

𝟓, 𝟑)

𝐿𝑅1𝐷𝐸𝑅 ℎ +𝑏2

𝑎, 𝑘 + 𝑐 → 𝐿𝑅1𝐷𝐸𝑅(0 +

4 2

5, 0 + 3)

𝑳𝑹𝟏𝑫𝑬𝑹𝟏𝟔

𝟓, 𝟑

Las coordenadas de los extremos del lado recto de abajo:

𝐿𝑅2𝐼𝑍𝑄(ℎ −𝑏2

𝑎, 𝑘 − 𝑐) y 𝐿𝑅2𝐷𝐸𝑅(ℎ +

𝑏2

𝑎, 𝑘 − 𝑐)

𝐿𝑅2𝐼𝑍𝑄 ℎ −𝑏2

𝑎, 𝑘 − 𝑐 → 𝐿𝑅2𝐼𝑍𝑄(0 −

16

5, 0 − 3)

𝑳𝑹𝟐𝑰𝒁𝑸(−𝟏𝟔

𝟓, −

𝟏𝟔

𝟓)

𝐿𝑅2𝐷𝐸𝑅 ℎ +𝑏2

𝑎, 𝑘 − 𝑐 → 𝐿𝑅2𝐷𝐸𝑅(0 +

(4)2

5, 0 − 3)

𝐿𝑅2𝐷𝐸𝑅16

5, −

16

5

SIGUIENTEANTERIOR

La gráfica es la siguiente:

ANTERIOR IR AL MENU

SOLUCIÓN 3

Datos del

problema:

𝟒𝒙𝟐 + 𝒚𝟐 − 𝟑𝒙 + 𝟒𝒚 − 𝟖 = 𝟏𝟎

𝟒𝒙𝟐 + 𝒚𝟐 − 𝟑𝒙 + 𝟒𝒚 − 𝟖 = 𝟏𝟎(𝟒𝒙𝟐 − 𝟑𝒙) + (𝒚𝟐+𝟒𝒚) = 𝟏𝟎 + 𝟖

𝟒(𝒙𝟐 −𝟑

𝟒𝒙) + (𝒚𝟐+𝟒𝒚) = 𝟏𝟖

𝟒 𝐱𝟐 −𝟑

𝟒𝐱 +

𝟗

𝟔𝟒−

𝟗

𝟔𝟒+ 𝐲𝟐 + 𝟒𝐲 + 𝟒 − 𝟒 = 𝟏𝟖

𝟒 𝒙 −𝟑

𝟖

𝟐−

𝟗

𝟏𝟔+ 𝒚 + 𝟐 𝟐 − 𝟒 = 𝟏𝟖

𝟒 𝒙 −𝟑

𝟖

𝟐+ 𝒚 + 𝟐 𝟐 = 𝟐𝟐 +

𝟗

𝟏𝟔=

𝟑𝟓𝟐

𝟏𝟔

𝟒 𝒙 −𝟑

𝟖

𝟐+ 𝒚 + 𝟐 𝟐 =

𝟑𝟔𝟏

𝟏𝟔

𝟒 𝒙−𝟑

𝟖

𝟐

𝟑𝟔𝟏

𝟏𝟔

+𝒚+𝟐 𝟐

𝟑𝟔𝟏

𝟏𝟔

=𝟑𝟔𝟏

𝟏𝟔𝟑𝟔𝟏

𝟏𝟔

→𝒙−

𝟑

𝟖

𝟐

𝟑𝟔𝟏

𝟔𝟒

+𝒚+𝟐 𝟐

𝟑𝟔𝟏

𝟏𝟔

= 𝟏 donde se

tiene que:𝟑𝟔𝟏

𝟏𝟔>

𝟑𝟔𝟏

𝟔𝟒por tanto, la ecuación es de

la forma𝒙−𝒉 𝟐

𝒃𝟐+

𝒚−𝒌 𝟐

𝒂𝟐= 𝟏, que representa una

ecuación de la elipse vertical de centro C(h,k), es

decir C(3/8;-2), donde además tenemos que los

ejes mayor y menor son:

𝒂𝟐 =𝟑𝟔𝟏

𝟏𝟔→ 𝒂 = ±

𝟏𝟗

𝟒; 𝒃𝟐 =

𝟑𝟔𝟏

𝟔𝟒→ 𝒃 = ±

𝟏𝟗

𝟖y «c» lo

obtenemos mediante el teorema de Pitágoras:

𝒂𝟐 = 𝒃𝟐 + 𝒄𝟐 → 𝒄𝟐 =𝟑𝟔𝟏

𝟏𝟔−

𝟑𝟔𝟏

𝟔𝟒=

𝟏𝟎𝟖𝟑

𝟔𝟒→ 𝒄 = ±

𝟏𝟗

𝟖𝟑

Desarrollamos y operamos, agrupamos términos de

una misma variable, se completa cuadrado perfecto

y se agrupan las constante hacia el otro miembro:

IR AL MENU SIGUIENTE

Las coordenadas de los vértices mayores y menores son:

𝑉2 ℎ, 𝑘 − 𝑎 𝑦 𝑉1 ℎ, 𝑘 + 𝑎 → 𝑉23

8; −2 −

19

4𝑦 𝑉1

3

8; −2 +

19

4

𝑉23

8; −

27

4𝑦 𝑉1

3

8;11

4

𝐵2(ℎ − 𝑏, 𝑘); 𝐵1 ℎ + 𝑏, 𝑘 → 𝐵2(−16

8, −2) y 𝐵1

3

8+

19

8, −2

𝐵2 −2,−2 y B111

4; −2

Las coordenadas de los focos son:

𝐹2 ℎ, 𝑘 − 𝑐 ; 𝐹1 ℎ, 𝑘 + 𝑐 → 𝐹23

8; −2 −

19

83 ; 𝐹1

3

8; −2 +

19

83

𝐹23

8; −

16+19 3

8; 𝐹1

3

8;19 3−16

8

Las directrices son:

𝐷: 𝑘 ±𝑎2

𝑐→

𝐷1: 𝑦1 = 𝑘 +𝑎2

𝑐→ 𝐷1: 𝑦1 =

19 3 − 12

6

𝐷2: 𝑦2 = 𝑘 −𝑎2

𝑐→ 𝐷2: 𝑦2 = −

19 3 + 12

6Los lados rectos son:

Lado recto superior: 𝐿𝑅𝐴𝐵 = 2𝑏2

𝑎→ 𝐿𝑅𝐴𝐵 =

219

8

2

19

4

=2·192·4

64·19=

19

8

Lado recto inferior: 𝐿𝑅𝐷𝐸 = 2𝑏2

𝑎→ 𝐿𝑅𝐷𝐸 =

2(19

4)

19

2

=2·19

2·19=

19

8

Las Coordenadas de los extremos de los lados rectos

𝐿𝑅1𝐼𝑍𝑄(ℎ −𝑏2

𝑎, 𝑘 + 𝑐) y 𝐿𝑅1𝐷𝐸𝑅(ℎ +

𝑏2

𝑎, 𝑘 + 𝑐)

𝐿𝑅1𝐼𝑍𝑄3

8−

19

4

2

19

2

, −2 +19 3

8→ 𝑳𝑹𝟏𝑰𝒁𝑸(−

𝟏𝟑

𝟏𝟔,𝟏𝟗 𝟑−𝟏𝟔

𝟖)

𝐿𝑅1𝐷𝐸𝑅3

8+

19

4

2

19

2

, −2 +19 3

8→ 𝑳𝑹𝟏𝑫𝑬𝑹

𝟐𝟓

𝟏𝟔,𝟏𝟗 𝟑−𝟏𝟔

𝟖

SIGUIENTEANTERIOR

La gráfica del problema planteado es:

𝐿𝑅2𝐼𝑍𝑄(ℎ −𝑏2

𝑎, 𝑘 − 𝑐) y 𝐿𝑅2𝐷𝐸𝑅(ℎ +

𝑏2

𝑎, 𝑘 − 𝑐)

𝐿𝑅2𝐼𝑍𝑄 −13

16, −

19 3+16

8→ 𝑳𝑹𝟐𝑰𝒁𝑸(−

𝟏𝟑

𝟏𝟔, −

𝟏𝟗 𝟑+𝟏𝟔

𝟖)

𝐿𝑅2𝐷𝐸𝑅25

16, −

19 3+16

8→ 𝑳𝑹𝟐𝑫𝑬𝑹

𝟐𝟓

𝟏𝟔, −

𝟏𝟗 𝟑+𝟏𝟔

𝟖

ANTERIOR IR AL MENU

SOLUCIÓN 4

Datos del

problema:

𝟏𝟔𝒙𝟐 + 𝟐𝟓𝒚𝟐 − 𝟒𝟖𝒙 + 𝟏𝟎𝟎𝒚 − 𝟐𝟔𝟒 = 𝟎

Desarrollamos y operamos, agrupamos términos de

una misma variable, se completa cuadrado perfecto

y se agrupan las constante hacia el otro miembro:

(𝟏𝟔𝒙𝟐 − 𝟒𝟖𝒙) + (𝟐𝟓𝒚𝟐+𝟏𝟎𝟎𝒚) = 𝟐𝟔𝟒𝟏𝟔(𝒙𝟐 − 𝟑𝒙) + 𝟐𝟓(𝒚𝟐 + 𝟒𝒚) = 𝟐𝟔𝟒

𝟏𝟔 𝒙𝟐 − 𝟑𝒙 +𝟗

𝟒−

𝟗

𝟒+ 𝟐𝟓 𝒚𝟐 + 𝟒𝒚 + 𝟒 − 𝟒 = 𝟐𝟔𝟒

𝟏𝟔 𝒙𝟐 − 𝟑𝒙 +𝟗

𝟒− 𝟑𝟔 + 𝟐𝟓 𝒚𝟐 + 𝟒𝒚 + 𝟒 − 𝟏𝟎𝟎 = 𝟐𝟔𝟒

𝟏𝟔 𝒙 −𝟑

𝟐

𝟐+ 𝟐𝟓 𝒚 + 𝟐 𝟐 = 𝟐𝟔𝟒 + 𝟏𝟎𝟎 + 𝟑𝟔

𝟏𝟔 𝒙 −𝟑

𝟐

𝟐+ 𝟐𝟓 𝒚 + 𝟐 𝟐 = 𝟒𝟎𝟎

𝟏𝟔 𝒙−𝟑

𝟐

𝟐

𝟒𝟎𝟎+

𝟐𝟓 𝒚+𝟐 𝟐

𝟒𝟎𝟎=

𝟒𝟎𝟎

𝟒𝟎𝟎→

𝐱−𝟑

𝟐

𝟐

𝟐𝟓+

𝐲+𝟐 𝟐

𝟏𝟔= 𝟏, que es de la

forma𝐱−𝒉 𝟐

𝐚𝟐+

𝐲−𝐤 𝟐

𝐛𝟐= 𝟏, es decir, la ecuación de la elipse

horizontal con centro C(h,k) = 𝐶(3

2, −2). 𝑎2 = 25; 𝑎 = ±5, 𝑏2 =

16; 𝑏 = ±4A «c» lo obtenemos mediante la relación Pitagórica para las

elipses, es decir: 𝒂𝟐 = 𝒃𝟐 + 𝒄𝟐 → 𝒄𝟐 = 𝒂𝟐 − 𝒃𝟐; 𝒄 = ±𝟑

La excentricidad es: 𝑒 =𝑐

𝑎→ 𝑒 =

3

5< 1

Las coordenadas de los vértices mayor y menor son:

𝑉2 ℎ − 𝑎, 𝑘 ; 𝑉1 ℎ + 𝑎, 𝑘 → 𝑉2 −7

2, −2 ; 𝑉1

13

2, −2

𝐵2 ℎ, 𝑘 − 𝑏 ; 𝐵1 ℎ, 𝑘 + 𝑏 → 𝐵23

2, −6 ; 𝐵1

3

2, 2

Las coordenadas de los focos:

𝐹2 ℎ − 𝑐, 𝑘 ; 𝐹1 ℎ + 𝑐, 𝑘 → 𝐹2 −3

2, −2 ; 𝑉1

9

2, −2

IR AL MENU SIGUIENTE

La gráfica del problema planteado es:

Las directrices de la elipse horizontal tienen las ecuaciones siguientes:

𝑥 = ℎ ±𝑎2

𝑐→

𝑥2 = ℎ −𝑎2

𝑐

𝑥1 = ℎ +𝑎2

𝑐

𝐷1: 𝑥 =3

2+

25

3=

9+50

6→ 𝐷1: 𝑥 =

59

6

𝐷2: 𝑥 =3

2−

25

3=

9−50

6→ 𝐷2: 𝑥 = −

41

6

El lado recto viene dado por: 𝐿𝑅 =2𝑏2

𝑎→ 𝐿𝑅 =

2(4)2

5→ 𝐿𝑅 =

32

5

Las coordenadas de los extremos de los lados rectos son:

Lado Izquierdo Lado Derecho

𝐿𝑅𝐼𝐴𝑅(ℎ − 𝑐, 𝑘 +𝑏2

𝑎) 𝐿𝑅𝐷𝐴𝑅(ℎ + 𝑐, 𝑘 +

𝑏2

𝑎)

𝐿𝑅𝐼𝐴𝑅(−3

2,16

5) 𝐿𝑅𝐷𝐴𝑅(

9

2,16

5)

𝐿𝑅𝐼𝐴𝐵(ℎ − 𝑐, 𝑘 −𝑏2

𝑎) 𝐿𝑅𝐷𝐴𝐵(ℎ + 𝑐, 𝑘 −

𝑏2

𝑎)

𝐿𝑅𝐼𝐴𝐵(−3

2, −

16

5) 𝐿𝑅𝐷𝐴𝐵(

9

5, −

16

5)

ANTERIOR IR AL MENU