LA CIRCUNFERENCIA

Es un lugar geométrico de un conjunto infinito de puntos que equidistan de un punto situado en el centro

ELEMENTOS DE LA CIRCUNFERENCIA

PROPIEDADES BÁSICAS DE LA CIRCUNFERENCIA

1.-el radio trazado al punto de tangencia es perpendicular a la recta tangente

2.-radio o diámetro perpendicular a una cuerda la biseca (divide en dos segmentos iguales)

3.-cuerdas paralelas determinar arcos congruentes entre las paralelas

4.-a cuerdas congruentes en una misma circunferencia les corresponde arcos congruentes

POSICIONES RELATIVAS DE DOS CIRCUNFERENCIAS

1.-circunferencias concéntricas tienen el mismo centro

2.-circunferencias exteriores no tiene punto en común

http://es.slideshare.net/guest29f6ed0/circunferencia213-ro-secundaria-1199198

ECUACIÓN DE LA CIRCUNFERENCIADefinición.- Una circunferencia es el lugar geométrico del conjunto de puntos en un plano tales que las distancia a cada uno de ellos desde un punto fijo del plano es una constante.El punto fijo se llama centro de la circunferencia, y la distancia constante se llama radio.

1. Formas de la ecuación de una circunferenciaLa ecuación de una circunferencia con centro en C(h,k) y radio igual a r es:

y

O x

rP(x;y)

C(h;k)

(x-h)2 + (y-k)2 = r2

1.1. Si el centro de una circunferencia de radio r está en el origen, la ecuación de la circunferencia se reduce a:

x2+y2 = r2

Ecuación que se conoce como la forma canónica de la ecuación de una circunferencia.

2. Forma general de la ecuación de la circunferenciaSi se suprimen los paréntesis en la ecuación ordinaria de una circunferencia, tenemos:x2+y2–2hx – 2ky + h2 + k2 – r2 = 0 (1)Esta ecuación tiene la misma forma que:x2 + y2 + Dx + Ey + F =0 (2)

La ecuación (2) se llama forma general de la ecuación de una circunferencia.

La ecuación:

x2 + y2 + Dx + Ey + F = 0 representa una circunferencia de radio, r 0, solamente si:D2+E2-4F>0

Las coordenadas del centro son entonces, (−D2 ,−E2 )

y el radio r=12

√D2+E2−4 F

Demostración:En efecto, complementando para las variantes x e y se tiene:

(x2+Dx+ D24 )+( y2+Ey+E24 )=−F+ D2

4+E

2

4

+(x+ D2 )2

+( y+ E2 )2

= 14

(D2+E2−4 F ) (3)

Pueden ocurrir tres casos para que (3) pueda o no representar una circunferencia.

a) Si D2+E2 – 4F > 0, entonces (3) representa una circunferencia de centro C (−D2 ,− E2 )

y radio r=12

√D2+E2−4 F

b) Si D2+E2 -4F = 0, entonces (3) representa un punto de coordenadas C (−D2 ,− E2 )

.c) Si D2+E2 – 4F < 0, entonces, la ecuación (3) representa un conjunto vacío , es decir,

no representa un lugar geométrico.

EJERCICIOS PROPUESTOS

01. La ecuación de la circunferencia con centro en (3; −5 ) y radio 6, es:

A) ( x+3)2+( y−5 )2=36

B) ( x−3 )2+( y+5 )2=36

C) ( x−3 )2+( y−5)2=36

D) ( x+3)2+( y+5 )2=36

E) ( x−5 )2+( y+3 )2=36

02. Determine las coordenadas del centro y el radio de una circunferencia cuya ecuación es:

( x−7 )2+( y+4 )2=64

A) (4; 7) ; r = 4

B) (−4 ; 7) ; r = 8C) (7; 4) ; r = 64

D) (7; −4 ) ; r = 8

E) (−7 ; 4) r = 16

03. Halle la ecuación de la circunferencia con centro en el origen del sistema de

coordenadas rectangulares y que asa por el punto (−1 ; 3).

A) x2+ y2=3

B) x2+ y2=10

C) x2+ y2=4

D) x2+ y2=9

E) x2+ y2=2

04. Halle la ecuación general de la circunferencia con centro en (5; −3 ) y radio 6.

A) x2+ y2+10x+6 y+2=0

B) x2+ y2−10 x−6 y−2=0

C) x2+ y2+10x−6 y+2=0

D) x2+ y2−10 x+6 y−2=0

E) x2+ y2−10 x−6 y+2=0

05. Halle las coordenadas del centro y el radio de una circunferencia cuya ecuación es:

x2+ y2+8 x−14 y+40=0

A) (2; 7) ; r = 4B) (4; 5) ; t = 5

C) (−3 ; 4) ; r = 6

D) (−4 ; 7) ; r = 5

E) (4; −7 ) ; r = 5

06. Determine la ecuación general de la circunferencia con centro en (−3 ; 2) y que pasa

por el punto (5; −6 ).

A) x2+ y2+16 x−4 y+115=0

B) x2+ y2+6 x−4 y−115=0

C) x2+ y2−6 x−4 y−115=0

D) x2+ y2+3x−2 y+128=0

E) x2+ y2+12x−8 y+65=0

07. Hallar la ecuación de la circunferencia de diámetro el segmento de extremos (2; 5) y

(−4 ; −3 ).

A) ( x+1 )2+( y−1 )2=25

B) ( x−1 )2+ ( y−1 )2=25

C) ( x−1 )2+ ( y+1 )2=25

D) ( x−2 )2+ ( y+5 )2=25

E) ( x+4 )2+( y+3 )2=25

08. Halle el radio y las coordenadas del centro de la circunferencia cuya ecuación es:

x2+ y2−4 x+12 y−20=0A) r = √2 ; (3; −2 )

B) r = √15 ; (4 ; 3)

C) r = √15 ; (3 ; −2 )

D) r = 2√15 ; (2 ; −6 )

E) r = 3√15 ; (4 ; 3)

09. Encontrar los puntos de intersección de la circunferencia: x2+ y2−8 x+8 y−9=0 con

el eje Y⃗ .

A) (0; 3) y (0; 6) B)(0 ; 5) y (0 ; 4)

C) (0; −9 ) y (0 ;1)

D)(0;−3 ) y (0;−2 )

E) (0; −7 ) y (0; −2 )

10. Halle el área del cuadrado inscrito en la circunferencia de ecuación: x2+ y2=16

A)4 μ2

B)16 μ2

C)32μ2

D)64 μ2

E)72μ2

11. Calcular la distancia del punto M(27; 5) a la circunferencia: x2+ y2−6 x+4 y−23=0 .

A)15B)17C)19D)14E)25

12. Hallar la ecuación de una circunferencia cuyo centro es (−2 ; 3) y su radio es 5.

A) ( x−2 )2+ ( y+3 )2=25

B) ( x+3 )2+ ( y−2 )2=25

C) ( x+3 )2+ ( y+2 )2=25

D) ( x−2 )2+ ( y−3 )2=25

E) ( x+2 )2+( y+3 )2=25

13. La ecuación de una circunferencia es: ( x+4 )2+( y+3 )2=36 . Calcular su radio y las coordenadas del centro.A) (−2 ; −3 ); r = 3

B) (−3 ; −4 ) ; r = 4

C) (−4 ; −3 ) ; r = 6

D) (−3 ; 4) = r = 2E) (3; 4) ; r = 3

14. Hallar la ecuación de la circunferencia cuyo centro es el origen de coordenadas y que pasa por (3; 4).

A)x2+ y2=3

B)x2+ y2=4

C)x2+ y2=25

D)x2+ y2=16

E)x2+ y2=9

15. Hallar la ecuación general de la circunferencia de radio igual a 7 y cuyo centro es (5; −1 ).

A) x2+ y2+10x−2 y+23=0

B) x2+ y2−10 x+2 y−23=0

C) x2+ y2−10 x−2 y−23=0

D) x2+ y2+10x+2 y−23=0

E) x2+ y2+10 x+2 y+23=0

16. Hallar la ecuación general de la circunferencia cuyo centro es (−2 ; 3) y pasa por el punto (4; 5).

A) x2+ y2+2x+6 y+12=0

B) x2+ y2−3 x−5 y+26=0

C) x2+ y2+4 x−6 y+27=0

D) x2+ y2−3 x+6 y+27=0

E) x2+ y2+3x+4 y+31=0

17. Halle la ecuación de la circunferencia con centro en el origen del sistema de coordenadas rectangulares y de diámetro 18.

A)x2+ y2=3 B)x

2+ y2=9

C)x2+ y2=18 D)x

2+ y2=27

E)x2+ y2=81

18. Halle la ecuación de la circunferencia tangente al eje X⃗ y cuyo centro es el punto de intersección de la recta:

X – 2y + 8 = 0 con el eje Y⃗ .

A) x2+ y2−8 y=0

B) x2+ y2−8 x=0

C) x2+ y2−4 y=0

D) x2+ y2−4 x=0

E) x2+ y2−16 y=0

T

V p

X

P(x; y)

EY

O

(h, k)

LD

H

F(h + p; k)ph – p

LA PARÁBOLA

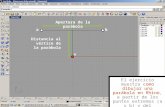
Es el lugar geométrico de los puntos de un plano que equidistan de un punto y de una recta del mismo plano. El punto se denomina foco y la recta directriz.

Vértice : V(h ; k)

Foco : F

Directriz : L⃗D

Eje Focal : L⃗Cuerda : MN

Cuerda Focal : EQ

Lado recto : AB

Se denomina parámetro de la parábola a la distancia (VF = p) que hay entre el vértice y el foco.

Se cumple:

VF = VH

ECUACIÓN DE LA PARÁBOLA

Ecuación de la parábola de vértice V(h; k) y cuyo eje es paralelo al eje x.

LD

NB

Q

AE M

LFVH

Punto genérico: P(x; y)Parámetro de la parábola: pSegún el gráfico: PH + HT = PT

PH + h – p = x

HP = x – h + p

Condición de lugar geométrico.PF = PH

√ ( x−h−p )2+( y−k )2=x−h+ pElevando al cuadrado y reduciéndole se obtiene la ecuación ordinaria.

( y−k )2=4 p ( x−h )

Desarrollando la ecuación ordinaria ( y−k )2=4 p ( x−h ) se obtiene la Ecuación General de la parábola.

y2+Ay+Bx+C=0

Si la parábola se abre hacia la izquierda, entonces su ecuación es:

Vértice : V (h; k)Foco : FParámetro : p

( y−k )2=−4 p ( x−h )ecuación ordinaria

Ecuación canónica de la parábolaSi el vértice de la parábola coincide con el origen de coordenadas entonces las ecuaciones de la parábola que se abre a la derecha o izquierda son respectivamente.

y2=4 px

Foco : F

V(h; k)

LDY

X

F

Y

X

F

Y

X

F

y2=−4 px

Foco : F

Ecuación de la parábola de Vértice V(h; k) y cuyo eje es paralelo al eje y

Punto genérico : P (x; y)Parámetro de la Parábola : pSegún el gráfico :PH + HT = PT

PH + k – p = y PH = y – k + p

Condición de lugar geométricoPF = PH

√ ( x−h )2+( y−k−p )2= y−k+pElevando al cuadrado se obtiene la ecuación ordinaria.

( x−h )2=4 p ( y−k )

Desarrollando la ecuación ordinaria se obtiene la ecuación general de la parábola.

x2+Ax+By+C=0

Si la parábola se abre hacia abajo su ecuación es:

Vértice : V (h; k)Foco : FParámetro : p

( x−h )2=−4 p ( y−k )

Ecuación Canónica

V(h;

F(h; k+p)

P(x;

P

Y

N

XTO

Directriz

Foco

V(h; k)Y

X

F

Si el vértice coincide con el origen de coordenadas entonces las ecuaciones son respectivamente.

Foco : F

x2=4 py

Foco: F

x2=−4 py

PRÁCTICA DE AULA

01. Encuentre las coordenadas del foco y la ecuación de la directriz de la parábola.

y2=6 xA) (0, 3/2) ; y = -3/2B) (3/2, 0) ; y = -3/2C) (0, 2/3) ; y = -2/3D) (0, -2) ; y = 2E) (0, 2) ; y = -2

02. Encuentre las coordenadas del foco y la ecuación de la directriz.

y2=−20 xA) (3/4, 0) ; x = -3/4B) (5/4, 0) ; x = -5/4C) (-3/4, 0) ; x = 3/4D) (-5/4, 0) ; x = 5/4E) (-5, 0) ; x = 5

03. Encuentre la ecuación canónica de la parábola con foco en (3, 0)A) y2 = 10x

B) y2 = -10x

C) y2 = 12xD) y2 = -12xE) y2 = 9x

04. Hallar la ecuación de la parábola con foco (0, 4) y directriz D: y + 4 = 0A) x2 = 16yB) y2 = 3xC) x2 = 4yD) x2 = yE) y2 = 16x

Y

X

F

Y

XF

05. Hallar la ecuación de la parábola con V = (0, 0) y foco F(-2, 0)A) y2 = 8xB) y2 = -8xC) y2 = 4xD) y2 = -4xE) N.A.

06. Determinar el vértice V y el foco F de la parábola x = 2y2.A) F = (8, 0) y V = (0, 5)B) F(0, 8) y V = (5, 0)

C) F = ( 18 ,0) y V = (0, 0)

D) F = ( 18 , 18 ) y V = (1, 1)

E) N.A.

07. Una parábola cuyo vértice está en el origen y su eje coincide con el eje Y, pasa por el punto (6; -3). Determinar la ecuación de la parábola las coordenadas del foco y la ecuación de la directriz.A) x2 = -12y y = 3B) x2 = 12y y = 3C) x2 = y y = 5D) x2 = 12y y = -3E) N.A.

08. Una parábola cuyo vértice está en el origen y cuyo eje coincide con el eje Y y pasa por el punto (4, – 2). Hallar la ecuación de la parábola, las coordenadas de su foco, la ecuación de su directriz y la longitud de su lado recto.

A)x2=8 y , F=(0,– 2) , y=2, lado recto = – 8

B)x2=−8 y , F=(0,– 2) , y=2, lado recto = 8

C)x2=4 y , F=(1, 2) , y=3, lado recto = 4

D)x2=−4 y , F=(2,0) , y=–2, lado recto = 3

E) N.A.

09. Hallar la ecuación de la parábola de vértice en el origen y directriz la recta y – 5 = 0.

A)x2=5 y

B)x2=4 y

C)x2=20 y

D)x2=−20 y

E)x2=−5 y

10. Hallar la ecuación de la parábola cuyo vértice es el punto (3; 4) y cuyo foco es el punto (3, 2). Hallar también la ecuación de su directriz y la longitud de su lado recto.

A) ( x−3 )2=8( y−4 ), L.R = 8, y = 6

B) ( x−3 )2=8( y+4 ) , L.R = 8, y = 0

C) ( x+3)2=−8 ( y−4 ) , L.R = –8, y =–6

D) ( x−3 )2=−8( y−4 ), L.R = 8, y = 6

E) N.A.

11. Hallar la ecuación de la parábola cuyo vértice es el origen sabiendo que es simétrica respecto al eje y, y que pasa por el punto Q = (4; – 8)

A)2x2+ y=0

B)x2+ y

2=0

C)x2+ y=0

D)x2+2 y=0

E)N.A.

12. Hallar la ecuación de la parábola que tenga por foco F = (– 5/3, 0) y directriz la recta D: 3x – 5 = 0

A)3 y2+20 x=0

B)3 y2−20 x=0

C)y2+20x=0

D)y2=x

E)20 y2−3 x=0

13. Determinar los elementos de la parábola de ecuación x2=8 y .

A) F = (0, 2), D: y = – 2, L.R. = 8B) F = (0, 2), D: y = 1, L.R. = 4C) F = (0, – 2), D: y = 1, L.R. = 4D) F = (1, 2), L.R. = 3E) N.A.

14. Determinar la ecuación de la parábola de Foco F = (3, 0) y directriz x + 3 = 0.

A)y2=3 x

B)y2−3 x

C)x2=3 y

D)x2=−3 y

E) y2=12 x

15. Determinar los elementos de la parábola de ecuación y2−4 y−8 x+28=0

A) V = (3;–2), L.R = 8, F = (5, 2), D: x = 1B) V = (3; 2), L.R = 8, F = (5, 2), D: x = -1C) V = (3;2), L.R = 8, F = (5, 2), D: x = 1D) V = (–3;2), L.R = -8, F = (5,2), D=x = 1E) N.A.

16. Determinar la ecuación de la parábola de foco F = (1, 3) y vértice V = (– 2, 3)

A)x2=5 y

B)y2=5 x

C)y2=6 x

D)y2−6 y−12 x−15=0

17. Determinar la ecuación del lugar geométrico de todos los puntos (x, y) del plano que equidistan del punto F(2, 2) y del eje de las abscisas.

A) ( x−2 )2=4( y−1)

B) ( x+2)2=4 ( y+1)

C) ( x−2 )2=4( y+1 )

D) ( x+2)2=−4 ( y+1)

E) ( x−2 )2=−4( y+1 )