Instituto Universitario Politécnico

“Santiago Mariño”

Extensión Valencia

Escuela de Ingeniería de Sistemas

Autor:

Emir Aguilera C.I.: 12.063.839

Escuela “47”

Valencia, Julio de 2012

Ecuaci

ón

Difere

ncial

Ordin

arias

(EDO)

Índice

Introducción

Ecuación Diferencial Ordinarias

Introducción

En diferentes áreas de la ciencia, y sobre todo en la ingeniería, se desarrollan modelos

matemáticos para ayudar a comprender la fenomenología o el origen de ciertos

problemas físicos, biológicos, sociales, etc. Estos modelos, por lo general, pueden ser

expresados a partir de ecuaciones que contiene ciertas derivadas de una función

desconocida. A una ecuación de este tipo se le denomina ecuación diferencial.

La historia de las ecuaciones diferenciales comenzó en el siglo XVI, donde los

matemáticos Newton, Leibniz y los hermanos Bernoulli resolvieron las primeras

ecuaciones diferenciales sencillas a partir de unos problemas de Mecánica y Geometría.

De hecho, según Nápoles y otros (2002), a finales del siglo XVII James y Johan Bernoulli,

introducen término como el de “Integrar” una ecuación diferencial, así como la técnica de

variables separables para resolver una ecuación diferencial.

Estos primeros descubrimientos abrieron al mundo un universo de ecuaciones nuevas, así

como también a una serie de procedimientos que nos permiten la resolución de algunos

tipos de ecuaciones diferenciales que se presentan en problemas de modelado.

Actualmente, las ecuaciones diferenciales y los modelos matemáticos se han convertido

en un tema fundamental e indispensable para ser incluido en el pensum de estudio de

cualquier carrera de ingeniería a nivel mundial, trata sobre los tipos de ecuaciones

diferenciales, las técnicas como resolverlas y modelos matemáticos que las incluyen.

Ecuación Diferencial Ordinaria

Una ecuación diferencial es una ecuación en la que interviene una función incógnita y una

o varias de sus derivadas. Este tipo de ecuaciones aparece en el estudio de numerosos

fenómenos físicos y químicos: desintegración radiactiva, crecimiento de poblaciones,

reacciones químicas, problemas gravitatorios, etc. No es exagerado afirmar que la

naturaleza se describe por medio de ecuaciones diferenciales, de modo que un

conocimiento de esta última materia nos ayudaría a entender mejor los fenómenos

naturales. ´

Las ecuaciones diferenciales se pueden clasificar, básicamente, atendiendo a dos

criterios: ´

(1) TIPO: Si la función incógnita contiene una única variable independiente, entonces la

ecuación se denomina ecuación diferencial ordinaria, abreviadamente E.D.O. En otro

caso, cuando la función incógnita contiene dos o mas variables independientes, la

ecuación se dice que es una ecuación diferencial en derivadas parciales.

(2) ORDEN: Es la derivada de orden más alto que aparece en la ecuación diferencial.

Ecuaciones Diferenciales Ordinarias con Condiciones Iniciales

En este tipo de problemas, debemos obtener  valores aproximados de la

función solución de una ecuación diferencial en m puntos de un intervalo del dominio

de la misma, partiendo de condiciones iniciales conocidas de la función a

determinar en el extremo inicial del intervalo. En los denominados métodos de un paso,

que describiremos a continuación, el valor de la función en el primer punto interior del

intervalo se calcula a partir del valor conocido de la función en punto inicial del intervalo.

De la misma forma el valor de la función incógnita en el i-ésimo punto del dominio, xi, se

calcula a partir del valor de la función en el punto xi-1. A su vez la función en el punto

i+1 se calcula a partir del valor de la función en el punto i,

Es decir que se calcula la función en un punto cualquiera del intervalo

partiendo de la solución obtenida para el punto anterior, y así sucesivamente.

De esta manera, con la aplicación recurrente los algoritmos correspondientes a

cualquiera de estos métodos, a lo l a rgo de t odo e l i n t e r va lo de i n teg rac ión ,

se ob t i ene l a denominada t r ayec to r i a de l a solución. Los métodos que

estudiaremos están limitados a la solución de ecuaciones diferenciales ordinarias de

primer orden. Esto, que en principio parece una severa limitación de los

m ismos , no l o es t an to s i r eco rdamos que cua lqu ie r ecuación

diferencial ordinaria de orden n puede ser transformada en un sistema de n

ecuaciones diferenciales ordinarias de primer orden. Por otra parte el

procedimiento para obtener la solución de un sistema de EDOs de primer

orden es una sencilla extensión del procedimiento para obtener la solución de

una sola EDO por lo que estos métodos pueden ser aplicados sin ninguna

dificultad a la solución de EDOs de orden n. Dada una ecuación diferencial ordinaria de

primer orden de la forma:

La solución numérica tendrá la forma:

De acuerdo con esta ecuación, una pendiente estimada se usa para extrapolar desde un valor anterior yi a un nuevo valor yi+1 en una distancia h

Todos los denominados métodos de un paso, que veremos, se pueden expresar

en esta forma general, que solo va a diferir en la manera en la cual se estima la

pendiente.

Método de Euler

Se llama método de Euler al método numérico consistente en ir incrementando paso a paso

la variable independiente y hallando la siguiente imagen con la derivada.

La primera derivada proporciona una estimación directa de la pendiente en Xi

Donde f (Xi, Yi) es la ecuación diferencial evaluada en Xi y Yi, Tal estimación podrá

substituirse en la ecuación, nos queda que:

Esta fórmula es conocida como el método de Euler (punto medio). Se predice un nuevo

valor de Y por medio de la pendiente (igual a la primera derivada en el valor original de X).

Error para el método de Euler

La solución numérica de las ecuaciones diferenciales ordinarias (EDO) involucra dos tipos

de error.

1) Errores de Truncamiento, o discretizacion, causados por la naturaleza de las técnicas

empleadas para aproximar los valores de y.

2) Errores de Redondeo, que son el resultado del número limite de cifras significativas que

pueden retener una computadora.

Método de Euler Mejorado

Este método se basa en la misma idea del método anterior, pero hace un

refinamiento en la aproximación, tomando un promedio entre ciertas pendientes. 

La fórmula es la siguiente: 

Donde

Para entender esta fórmula, analicemos el primer paso de la aproximación, con

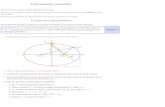
base en la siguiente gráfica: 

En la gráfica, vemos que la pendiente promedio  corresponde a la pendiente de 

la recta bisectriz de la recta tangente a la curva en el punto de la condición inicial y

la "recta tangente" a la curva en el punto  donde  es la aproximación

obtenida con la primera fórmula de Euler. Finalmente, esta recta bisectriz se

traslada paralelamente hasta el punto de la condición inicial, y se considera el

valor de esta recta en el punto como la aproximación de Euler mejorada.

Método de Euler Modificado

El método de Euler modificado trata de evitar este problema utilizando un valor

promedio de la derivada tomada en los dos extremos del intervalo. En lugar de la

derivada tomada en un solo extremo.

 

 

 EL METODO DE EULER MODIFICADO CONSTA DE DOS PASOS BASICOS:

 

1. Se parte de (xo,Yo) Y se utiliza el método de Euler a fin de calcular el valor

de Y correspondiente a Xl' Este valor de Y se denotará aquí como YI' ya que

sólo es un valor transitorio para Yl' Esta parte del proceso se conoce como

paso predictor.

2. El segundo paso se llama corrector, pues trata de corregir la predicción. En el

nuevo punto obtenido (XI, Yl) se evalúa la derivada [(xI' YI) usando la ecuación

diferencial ordinaria del PVI que se esté resolviendo; se obtiene la media

aritmética de esta derivada y la derivada en el punto inicial (xo' Yo)

 

 

1/2 [F(xo ,Yo) + F(Xl,YI)] = derivada promedio

 

Se usa la derivada promedio para calcular un nuevo valor de y1, con la ecuación

y1=y0+hf (x0, y0), que deberá ser mas exacto que y1

 

 

Y se tomara como valor definitivo de y1. Este procedimiento se repite hasta llegar a

yn.

El esquema iterativo para este método  quedara en general así:

Primero, usando el paso de predicción resulta:

 

Una vez obtenida yi+1 se calcula f(xi+1,yi+1), la derivada en el punto (xi+1,yi+1), y se

promedia con la derivada previa (xi,yi) para encontrar la derivada promedio

 

Se sustituye f(xi,yi) con este valor promedio en la ecuación de iteración de euler y

se obtiene:

 

Método de Heun:

Proporciona una variante al cálculo de la pendiente, dejando ésta como un

promedio entre la pendiente (o valor de la función) en un punto determinado y la

del punto posterior. Es un método que mejora la estimación de Euler, al estimar la

pendiente con dos derivadas para el intervalo h evaluado, una en el punto inicia y

la otra en el punto final. Este procedimiento se ilustra en la figura 2.

Un método para mejorar la estimación de la pendiente involucra la determinación y

promediado de dos derivadas para el intervalo (una en el punto inicial y otra en el

punto final).

Figura 2. Corrección de la pendiente con el método de Heun al usar dos derivadas. En a) predictor y b) corrector

En el método de Euler, la pendiente al inicio del intervalo se usa para extrapolar

linealmente ayi+1.

En el método de Heun la pendiente calculada en la estimación previa no es para la

respuesta final, sino para una predicción intermedia. Esta ecuación es

llamada predictor. Mejora una estimación de yi+1 que permite el cálculo de una

estimación de la pendiente al final del intervalo.

Aquí,  y0i+1  es el predictor, y es la misma ecuación de Euler para

encontrar  yi+1. Ésta nos sirve para calcular la pendiente y'i+1.

Las dos pendientes se promedian en el intervalo:

Esta pendiente promedio se utiliza para extrapolar linealmente

desde yi hasta yi+1 usando el método de Euler.

Esta ecuación es conocida como ecuación corrector. El método de Heun es un

procedimiento predictor – corrector.

Se puede conseguir una mejor precisión en el resultado si hacemos varios

procesos correctores, esto lo logramos tomando yi+1 y remplazándolo por y0i+1 en la

ecuación y así encontrar un nuevo yi+1, y se repite el proceso hasta donde se

desee. 

Método Polígono Mejorado:

Esta técnica es otra simple modificación del método de Euler. El método consiste

en usar el método de Euler para predecir un valor de y en el punto medio del

intervalo:

Este valor predicho se usa para calcular una pendiente en el punto medio del

intervalo:

Esta pendiente se considera como una pendiente promedio en todo el intervalo.

Luego con esta pendiente promedio estimada se extrapola linealmente desde xi

hasta xi+1:

Esta técnica no es iterativa puesto que yi+1 no

esta en ambos miembros de la ecuación corrector.

El error en el método del punto medio.

En un análisis similar que el realizado para el método de Heun se demuestra que

el método del polígono mejorado también es un método de segundo orden, que

tampoco requiere de la evaluación de derivadas superiores al primer orden.

También en este método los errores de truncamiento local y global son de orden O

(h3) y O (h2) respectivamente.

Métodos de Runge-Kutta:

Es el análisis y solución de los problemas de valor inicial de ecuaciones

diferenciales ordinarias (EDO), estos son una extensión del método de euler para

resolver las (EDO’S), pero con un orden de exactitud mas alto que este.

Bibliografía

HUERTA, Sarrate-Ramos, Rodríguez-Ferrán. Metodos Numericos, Introduccion

Aplicaciones y Propagacion. Edicions UPC. Primera Edición. 1998. Capítulo 9.

Páginas 201-202.