ESTALMAT-Andalucía Actividades 16/17estalmat/ACT/SESIONES/... · rectángulo áureo. Guarda el...
6
ESTALMAT-Andalucía Actividades 16/17 _________________________________________________________________________________________ F. Damián Aranda, Miguel de la Fuente y Manuel Gómez 1 de 6 Segundo Curso. Sesión: 13 Fecha: 04/02/2017 Título: Arte y Geometría INTRODUCCIÓN: Visualización de imágenes y videos donde muestren relaciones de la geometría y el arte: Uso de proporciones, Leyes de la perspectiva, Figuras imposibles, Obras de Escher, Fractales, etc. ACTIVIDAD 1: La proporción de un rectángulo. ¿Qué tienen en común estos rectángulos?, ¿Qué ocurre con sus diagonales? La proporción de un rectángulo es ___________________________________________________ La proporción de los rectángulos de esta página es ______________ Los rectángulos de la misma proporción anteriores tienen diagonales _________________________ Un cuadrado en realidad es un rectángulo de proporción ________________________ Naranja y Amarillo de Mark Rothko, 1956. A la derecha con trama geométrica superpuesta. 13’5 mm 9 mm 13 mm 19’5 mm 22 mm 33 mm 19 mm 28’5 mm 52’5 mm 35 mm
Transcript of ESTALMAT-Andalucía Actividades 16/17estalmat/ACT/SESIONES/... · rectángulo áureo. Guarda el...
ESTALMAT-Andalucía Actividades 16/17 _________________________________________________________________________________________
F. Damián Aranda, Miguel de la Fuente y Manuel Gómez 1 de 6
Segundo Curso.
Sesión: 13 Fecha: 04/02/2017 Título: Arte y Geometría INTRODUCCIÓN:
Visualización de imágenes y videos donde muestren relaciones de la geometría y el arte: Uso de proporciones, Leyes de la perspectiva, Figuras imposibles, Obras de Escher, Fractales, etc.
ACTIVIDAD 1: La proporción de un rectángulo. ¿Qué tienen en común estos rectángulos?, ¿Qué ocurre con sus diagonales?
La proporción de un rectángulo es ___________________________________________________
La proporción de los rectángulos de esta página es ______________
Los rectángulos de la misma proporción anteriores tienen diagonales _________________________
Un cuadrado en realidad es un rectángulo de proporción ________________________
Naranja y Amarillo de Mark Rothko, 1956. A la derecha con trama geométrica superpuesta.
13’5 mm
9 mm
13 mm
19’5 mm 22 mm
33 mm
19 mm
28’5 mm
52’5 mm
35 mm
ESTALMAT-Andalucía Actividades 16/17 _________________________________________________________________________________________
F. Damián Aranda, Miguel de la Fuente y Manuel Gómez 2 de 6
Rectángulo 3 Rectángulos DIN Rectángulo Cordobés Rectángulo áureo
Usando el lado de ciertos polígonos regulares y el radio de la circunferencia que lo circunscribe (como se muestra en las figuras superiores) podemos construir rectángulos de proporciones notables que se usan con frecuencia en arquitectura y arte. Los rectángulos DIN se usan además como formatos de papeles (esta hoja de papel que tienes en tus manos es un DIN A4). ACTIVIDAD 2: Si el lado menor es 1, ¿cuanto mide x, el lado mayor del rectángulo DIN?
(El teorema de Pitágoras puede ayudarte)
A continuación descargar el paquete de ficheros ARTE_GEOMETRIA_ESTALMAT_2017.zip usando el siguiente enlace: https://dl.dropboxusercontent.com/u/9113248/ARTE_GEOMETRIA_ESTALMAT_2017.zip
Descomprime su contenido en una carpeta que hayas creado previamente en el escritorio. ACTIVIDAD 3: Construcción de rectángulos de proporciones notables usando
Geogebra.
3.1. Construir un triángulo equilátero, un cuadrado, un pentágono regular, un octógono regular y un decágono regular a partir de uno de sus lados usando la herramienta “Polígono regular” de Geogebra. Hallar su centro1 usando el comando Baricentro[<Polígono>] . Guardar el fichero con el nombre “Polígonos regulares desde el lado y con centro”, para su uso posterior.
1 Aunque el Centro de un polígono regular se puede hallar de otro modo (como centro de dos vértices opuestos, en los de número par de
lados, o como punto de corte de las mediatrices de dos o más lados), lo haremos así por rapidez o por no incluir más líneas auxiliares en la construcción.
ESTALMAT-Andalucía Actividades 16/17 _________________________________________________________________________________________
F. Damián Aranda, Miguel de la Fuente y Manuel Gómez 3 de 6
3.2. Ocultar todos los polígonos excepto el octógono regular y construir a partir de él un Rectángulo Cordobés usando el lado del octógono como lado menor y el radio del octógono como lado mayor. Determinar con Geogebra su proporción. Guarda el fichero con el nombre “Rectángulo Cordobés”.
La vesica piscis (vejiga de pez en latín) es un símbolo hecho con dos círculos del mismo radio que se intersecan de manera que el centro de cada círculo está en la circunferencia del otro.
El rectángulo que la circunscribe es uno de proporción 3
La vesica piscis en un manuscrito medieval
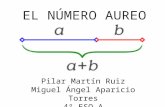
ACTIVIDAD 4: El rectángulo de oro. Buscando la proporción “ideal”. 4.1 ¿Qué proporción tiene el rectángulo que cumple que si se le añade un cuadrado por el lado
mayor se obtiene otro rectángulo de la misma proporción? 4.2 ¿Qué proporción tiene el rectángulo que colocando una pareja de ellos como se indica en la
figura que sigue abajo a la derecha (uno horizontal y otro vertical) la diagonal de uno pasa por un vértice del otro?
Planteemos las situaciones geométricas con la incógnita pertinente y averigüemos su valor:
Encuentra en cada figura la ecuación que tiene que cumplir x; verás que en ambos casos es la misma ecuación de 2º grado. Resuélvela y tendrás el valor de la proporción de dichos rectángulos, llamados rectángulos áureos o rectángulos de oro.
ESTALMAT-Andalucía Actividades 16/17 _________________________________________________________________________________________
F. Damián Aranda, Miguel de la Fuente y Manuel Gómez 4 de 6
A esta proporción x/1=x se le llama “número de oro” o “proporción áurea” y se representa por la letra griega (primera letra del nombre del escultor griego Fideas que, entre otras cosas, decoró el Partenón) 4.3. Acercándose al número iterativamente:
Resolver la ecuación x2=x+1 es equivalente a resolver la ecuación x=1+1/x, a cuya solución nos podemos acercar por un procedimiento iterativo del siguiente modo:
a) Usando una calculadora científica: Escribe 1 en la pantalla de tu calculadora y calcula su inverso (tecla de 1/x) luego suma 1 da a la tecla =; anota el resultado (que será 1/1+1=2) no lo borres y repite el proceso (tecla de 1/x) y luego +1= ; anota el resultado y repite el proceso,…. Los resultados formará una sucesión 1, 2, 1’5,…… síguela cuanto puedas. ¿A qué número nos acercamos cada vez más?.
b) Usando Geogebra:
Abre un fichero nuevo con Geogebra pon el Redondeo en 5 lugares decimales y escribe en la barra de entrada ListaIteración[1+1/x, 1, 10] y obtendrás como respuesta una lista con los diez primeros términos de la misma sucesión que hubieses obtenido haciéndolo con calculadora como en el apartado anterior.
El rectángulo áureo circunscribe el Partenón griego 4.4. Construyendo rectángulos áureos:
Abre el fichero Polígonos regulares desde el lado y con centro.ggb y oculta todos los polígonos excepto el pentágono regular y el decágono regular.
4.4.1. Construye un rectángulo usando el lado y la diagonal del pentágono. Determina con Geogebra su proporción comprobando que se trata de un rectángulo áureo. Guarda el fichero con el nombre “Rectángulo áureo”
4.4.2. Construye un rectángulo usando el lado y el radio del decágono recular. Determina con Geogebra su proporción comprobando que se trata de un rectángulo áureo. Guarda el fichero con el nombre “Rectángulo áureo”
La mitad del alumnado realizará 4.4.1 y la otra mitad 4.4.2
Así siempre que nos encontremos con el pentágono regular, con el decágono regular o con el dodecaedro podemos suponer que nos hemos encontrado indirectamente con el rectángulo áureo. ACTIVIDAD 5: Buscando rectángulos notables. Abre el fichero “3 rectangulos notables.ggb” y coloca dos puntos W=(0,0) y Z=(12,0). Inserta la imagen “PlanoMezquita(apaisado).jpg” usando la herramienta Inserta Imagen de Geogebra, pinchando en P como Esquina 1 y luego definiendo W como Esquina2.
ESTALMAT-Andalucía Actividades 16/17 _________________________________________________________________________________________
F. Damián Aranda, Miguel de la Fuente y Manuel Gómez 5 de 6
a) Mueve los rectángulos notables agarrándolos de A, B, C, D, E o F hasta superponerlos sobre zonas rectangulares del plano.
b) En lugar de hacerlo como en a) puedes situar los rectángulos notable con los lados paralelos a los ejes, trazar sus diagonales y usar paralelas y/o perpendiculares a ellas para localizar zonas rectangulares de la misma proporción sobre el plano y luego colocar sobre ellas los rectángulos notables correspondientes.
Guarda el fichero con el nombre “Proporciones notables en La Mezquita”
DECORACIONES PERIÓDICAS: MOSAICOS PERIÓDICOS Y FRISOS.
Algunas decoraciones y mosaicos tienen una característica que se llama periodicidad y es que pueden descomponerse en zonas iguales de forma que toda la decoración podría hacerse componiéndola con una de dichas zonas o figura básica sólo trasladando dicha figura en una o dos direcciones (sin someterla a giros ni reflexiones). En las figuras que siguen se aprecia dicha característica en la celosía izquierda y en el mosaico de la derecha, donde se han marcado las líneas paralelas que delimitan tales figuras básicas iguales. No ocurre así con el mosaico central; no es posible descomponerlo en zonas iguales trazando líneas paralelas en dos direcciones, por lo que no es periódico.
Si las figuras básicas se trasladan sólo en una dirección se obtiene una banda que se llama friso. La fotografía a la derecha de este párrafo contiene tres bandas friso. Cada friso puede descomponerse también en figuras básicas iguales por trazado de líneas paralelas de una sola dirección perpendiculares a la dirección de la banda.
ACTIVIDAD 6: Analizando la periodicidad. Abre el fichero “Trama vectorial.ggb” e inserta “Mosaico ESTALMAT.jpg” usando el punto P azul que tienes en la parte inferior izquierda como Esquina 1. Recoloca los puntos A, B y C para que la trama muestre la periodicidad del mosaico.
ESTALMAT-Andalucía Actividades 16/17 _________________________________________________________________________________________
F. Damián Aranda, Miguel de la Fuente y Manuel Gómez 6 de 6
ACTIVIDAD 7: Provocando la periodicidad. 7.1. Elimina el mosaico y quédate de nuevo con la trama vectorial de paralelogramos. Usa
traslaciones sucesivas de P con el vector u (o usa en la barra de herramientas el comando Secuencia[Traslada[P, n*u], n, 1, 5] para construir una trama friso de puntos.
7.2. Deshace esta acción y usa traslaciones sucesivas con los vectores u y v de P (o usa en la barra de herramientas el comando Secuencia[Traslada[Secuencia[Traslada[P, n*u], n, 1,5], m*v], m, 1, 4], para construir una trama periódica de puntos.
7.3. Deshace esta acción, Inserta MANZANA.png usando P como Esquina1. Ajusta la trama vectorial para que la manzana quede dentro de unos de los paralelogramos. Usa en la barra de herramientas el comando Secuencia[Traslada[imagen1, n*u], n, 1, 5] o Secuencia[Traslada[Secuencia[Traslada[imagen1, n*u], n, 1, 5], m*v], m, 1, 4] para construir un friso o un mosaico periódico con la manzana.
7.4. Si en lugar de MANZANA.png usas “Pieza 1 Mosaico ESTALMAT.png” y recolocas la trama en posición adecuada podrás reproducir el “Mosaico ESTALMAT.jpg” usando el comando correspondiente usado en 7.3.
ACTIVIDAD 8: Analizando transformaciones que superponen una decoración
sobre si misma. Abre el fichero Mosaico ESTALMAT para girar.ggb y coloca un punto C en el centro de una de las estrellas de 6 puntas de dicho mosaico. Gira el mosaico 60º respecto del punto C y recoloca con precisión el punto C hasta que observes cómo se superpone el mosaico con su girado. Como el mosaico se supone infinito en dos direcciones, se superpondría completamente consigo mismo y entonces decimos que C es un centro de giro de orden 6 (60º=360º/6) del mosaico. Por supuesto que hay infinitos centros de giro de orden 6 en este mosaico (al menos todos los centros de las estrellas). Estos puntos también son centros de giro de orden 3 (120º=360º/3) y de orden 2 (180º=360º/2) Los mosaicos periódicos siempre pueden superponerse sobre si mismos (permanecen invariantes) si se usan traslaciones adecuadas en dos direcciones distintas, como podrías comprobar. Las trasformaciones (movimientos) que los mantienen invariantes (que los superponen) permiten clasificarlos en 17 tipos distintos.
