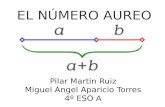
RECTÁNGULO ÁUREO

 

Un rectángulo especial es el llamado rectángulo áureo. Se trata de un rectángulo armonioso en sus dimensiones.

 Dibujamos un cuadrado y marcamos el punto medio de uno de sus lados. Lo unimos con uno de los vértices del lado opuesto y llevamos esa distancia sobre el lado inicial, de esta manera obtenemos el lado mayor del rectángulo.

 

 Si el lado del cuadrado vale 2 unidades, es claro que el lado mayor del rectángulo vale por lo

que la proporción entre los dos lados es:

 A este número se le llama número de oro, se representa por el símbolo Ø y su valor es 1,61803..., lo obtuvieron los griegos al hallar la relación entre la diagonal de un pentágono y el lado. El nombre de "número de oro" se debe a Leonardo da Vinci.

 

 En "el hombre ideal" de Leonardo, el cociente entre el lado del cuadrado y el radio de la circunferencia que tiene por centro el ombligo, es el número de oro.

 

 

 Otra propiedad de este rectángulo es que si se colocan dos iguales como en la figura de la derecha, se forma otro rectángulo áureo más grande.

 

.

 

Los egipcios ya conocían esta proporción y la usaron en la arquitectura de la pirámide de Keops (2600 años a.C.).

 

 Aparece en pinturas de Dalí, en la Venus de Boticelli. Esta razón también la usaron en sus producciones artistas del Renacimiento. En España, en la Alhambra, en edificios renacentistas como El Escorial ... y en la propia Naturaleza en las espirales de las conchas de ciertos moluscos.

 

Los griegos también la usaron en sus construcciones, especialmente El Partenón, cuyas proporciones están relacionadas entre sí por medio de la razón áurea.

 

El símbolo Ø para la relación áurea fue elegido por el matemático americano Mark Barr. La letra fue elegida porque era la primera del nombre de Phidias que solía usar la relación áurea en sus esculturas.

 

También se ha usado en el diseño del DNI, en la construcción de muebles, marcos para ventanas, camas, etc.

Un rectángulo cuyos lados están en una proporción igual a la razón áurea es llamado un rectángulo áureo. Este es un rectángulo muy especial como veremos. Los griegos lo consideraban de particular belleza y lo utilizaron asiduamente en su arquitectura. Al parecer a la mayoría de las personas también les parece más agradable a la vista un rectángulo con esas proporciones entre sus lados, inconscientemente se diseñan infinidad de cosas que resultan tener la forma de un rectángulo áureo: las hojas de papel tamaño carta miden 11 x 8 pulgadas, por ejemplo; esto nos da la proporción 1.37 que se parece a la razón aurea. Sólo por curiosidad, invitamos al lector a que mida y obtenga las proporciones de las ventanas de su casa, de su cuadro preferido, del mueble que más le agrada, muy probablemente serán rectángulos áureos.

Es fácil construir un rectángulo áureo a partir de un segmento de recta inicial como se puede ver en la animación.

El rectángulo áureo tiene una propiedad muy interesante. A partir de él podemos obtener una infinidad de nuevos rectángulos áureos. El proceso es iterativo (recursivo diría alguien dedicado a la computación) y consiste en quitar a cada rectángulo áureo un cuadrado, la superficie que queda luego de hacer esto es un nuevo rectángulo áureo. Este proceso se ilustra en la animación que aparece a continuación.

La proporción áurea se basa en una médida o número llamado también áureo, de oro, y representado por la letra griega φ (fi) (en minúscula) o Φ (fi) (en mayúscula). Es una proporción de más o menos: 2 + 1,6 , es decir, que una medida a=2 más otra medida b=1,618…. forman una medida que sumaría c= 3,618…. Aunque esta es la forma que yo me he inventado para acabar de comprender rápidamente esta proporción y para detectar que en una composición si que existe esta proporción áurea entre unas medidas a, b y c. Y que, por lo tanto, tienen este equilibrio mágico donde una medida contiene a otra más un poquito extra.

Medidas de la proporción áurea:

Dicen que el número áureo es un número irracional, que no encaja en las medidas exactas. Y efectivamente, porque la medida b es como un pequeño infinito, que nunca se acaba pero hacia más pequeño.

Fórmula del número áureo:

Esquemas visuales con la proporción áurea rectangular:

¿Cómo se dibuja la proporción áurea?

Paso a paso sencillo para dibujar esta proporción “divina” que aparece en multitud de formas naturales:

1. Se dibuja un cuadrado con una medida a.2. Desde la base inferior y en el centro de este cuadrado se crea un círculo que

debe tener de radio hasta las esquinas del propio cuadrado.3. Al hacer este círculo se sobrepasa la medida de a. Al continuar la recta inferior

del cuadrado y alcanzar el círculo, obtenemos la medida b. Ya tenemos el fragmento a + b.

4. Se traza el rectángulo vertical al lado de nuestro cuadrado. La unión de ambos es el rectángulo áureo primero.

5. Dentro del rectángulo y desde su esquina superior derecha podemos crear otro cuadrado, que tiene de medidas la sección b. Y a partir de este cuadrado segundo se inician otra vez todos los pasos, pues ahora debemos hayar la sección áurea de este nuevo cuadrado.

La espiral que construimos se llama Espiral áurea o de Fibonacci.

Dibujo con el sistema de dibujo de una proporción áurea rectangular. Formato SVG vectorial y ampliable.

Esquemas visuales con la proporción áurea triangular:

Llamado también el triángulo de Aristóteles o Logarítmico, contiene las dons medidas a y b. Para crear el triángulo se usan dos medidas a más una b. Dentro se desarrolla la espiral de Fibonacci igual que en los rectángulos.

Proporción áurea dentro de un triángulo. Formato SVG vectorial y ampliable.

Otras formas geométricas:

El decágono, que contiene 10 triángulos áureos. Formato SVG vectorial y ampliable.

Como yo no soy matemática y se me dan muy mal, si alguien quiere aportar información sobre la proporción áurea, genial, porque aún tengo mis dificultades para verla rápidamente en las proporciones.

Este tema continúa en Espirales áureas en las flores y plantas

RECTÁNGULO ÁUREO

  Un rectángulo cuyos lados están en una proporción igual a la razón áurea es

llamado un rectángulo áureo. Este es un rectángulo muy especial como

veremos. Los griegos lo consideraban de particular belleza y lo utilizaron

asiduamente en su arquitectura. Al parecer a la mayoría de las personas

también les parece más agradable a la vista un rectángulo con esas

proporciones entre sus lados, inconscientemente se diseñan infinidad de cosas

que resultan tener la forma de un rectángulo áureo. (Presentación Power point)

  Es fácil construir un rectángulo áureo a partir de un segmento de recta inicial,

trazarle la mediatriz, formar un cuadrado a partir del segmento y luego hacer

una circunferencia con radio el tramo que va desde el punto  medio del

segmento hasta el vértice superior derecho.

La Proporción Aurea, también conocida como Razón Aurea, Proporción Divina,

Número Dorado, etc. es aquella que cumple que la relación entre el sector

mayor y el sector menor es igual a la relación entre la suma de las partes y la

mayor de ellas.

O sea:

Vale aproximadamente ocho quintos.

· Esta relación numérica posee importantes propiedades matemáticas, fue

estudiada por Leonardo da Vinci, Luca Paccioli, Robin Cook, Johannes Kepler y

Pitágoras entre otros.

· Se dice que esta proporción es la esencia de la belleza, que aquellas figuras

que poseen la proporción aurea nos resultan las más bellas de todas las

formas, podemos apreciarla en la naturaleza por ej. en los caparazones de

ciertos moluscos: También se encuentra en el cuerpo humano, en las personas

de mayor atractivo.

 

 Se dibuja un cuadrado, desde el punto medio de una de sus aristas se gira el

vértice opuesto hasta la prolongación de la arista inicial.

 

Y=ab=ad. Siendo

e=punto medio de

ab

 

Existen muchos mitos acerca de que objetos de uso diario contienen las

medidas de un triángulo áurea como  el carnet de identidad, una tarjeta de

crédito o una cajetilla de tabaco, por eso nosotros en el siguiente espacio  lo

comprobaremos para así desmentir o afirmar un mito:

CARNET DE IDENTIDAD

 Para esta prueba usaremos un carnet de identidad de los antiguos y que aún

tienen validez, tal como este:

Sus medidas son de 4.5cm de ancho y 7.84cm de largo y en una representación

informática como la siguiente podemos observar que sus medidas no coinciden

con un rectángulo aurea.

Pincha sobre la imagen para agrandar

También lo podemos demostrar de forma analítica con los siguientes cálculos,

la división entre el largo y el ancho es, 7.84/4.5=1,7422222, por tanto no cumple

con un rectángulo áureo.

CAJETILLA DE TABACO

También supuestamente una cajetilla de tabaco posee las medidas de un

rectángulo áureo

Podemos observar en la siguiente fotografía que esto no es verdad pero sí que

es cierto que se parece bastante:

Pincha sobre la imagen para agrandar

TARJETA DE CRÉDITO. DNI ELECTRÓNICO

Otro ejemplo es una tarjeta de crédito de circulación legal por España. Sus

dimensiones coinciden con las del DNI electrónico ¿podría cumplir las medidas,

o No?

 

Como en los casos anteriores en este tampoco se cumple un rectángulo áureo

en su forma. Sus medidas son de 5.1cm de ancho y 8.25cm de largo.

8.25/5.1 =1,61764

Pincha sobre la imagen para agrandar

 

Por último podemos comprobar que las figuras que más se parecen son la de la

tarjeta y una cajetilla de tabaco, además es necesario decir que los cálculos

están afectados con un margen de error, pues las longitudes fueron medidas

con un calibre de precisión de ±o.o2cm

 

Un rectángulo se puede dividir en dos piezas: un cuadrado sobre el lado más corto y otro rectángulo. Para una determinada proporción de los lados del rectángulo inicial, usando este procedimieto obtenemos un rectángulo similar al inicial. Entonces tenemos un rectángulo áureo.

La proporción áurea A partir de la definición de Euclides de la división de un segmento en su razón media y extrema introducimos una propiedad de los rectángulos áureos y deducimos la ecuación y el valor de la proporción áurea. Si partimos de un rectángulo áureo el procedimiento se puede repetir indefinidamente.

La proporción áurea puede expresarse de esta manera: Un segmento se dice que está dividido en su razón extrema y media cuando el total del segmento es a la parte mayor como la parte mayor a la menor. (Euclides) Así podemos obtener el número áureo

El hecho de que el proceso de obtención de rectángulos áureos es infinito sugiere que el número áureo es inconmensurable, es decir, que el número áureo es irracional. Puesto que el lado de un pentágono regular y su diagonal están en proporción áurea y el pentágono y el pentagrama fueron los símbolos de los pitagóricos cabe la posibilidad de que se conociera que la diagonal de un pentágono y su lado son inconmensurables. Siendo éstos los primeros inconmensurables conocidos. Sin embargo, la primera demostración de la inconmensurabilidad de dos segmentos de la que tenemos constancia corresponde al lado y diagonal de un cuadrado (Euclides).

La diagonal de un pentágono regular y la razón áurea La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'. Podemos ver que el rectángulo ABDF y el rectángulo CDFH son semejantes y que CDFH se ha rotado un cuarto de vuelta.

Entonces

Llamaremos O al punto de intersección. Ahora podemos considerar la recta OC:

Puesto que

Entonces OC biseca el ángulo recto BOD

Análogamente

O está en la recta CG. Lo mismo para AE y entonces

Estas cuatro rectas, perpendiculares a pares, contienen todos los vértices de todos los infinitos rectángulos áureos. Cada pareja es la bisectriz de la otra pareja de rectas