Josue Tinoco Salvatierra Cdigo IB: 001110 0040

Conceptualizacin del nmero ureo y demostracin de su presencia en la secuencia de

Fibonacci, la arquitectura, la naturaleza y nosotros mismos.

Objetivos

Demostrar paso a paso la obtencin del nmero ureo.

Comprobar la magnitud de su presencia en diferentes reas, tales como biolgicas o artificiales.

Comprobar la validez de este nmero y su importancia.

Introduccin

La enorme utilidad de las matemticas en las ciencias naturales es algo que roza lo misterioso,

y no hay explicacin para ello. No es en absoluto natural que existan leyes de la naturaleza, y

mucho menos que el hombre sea capaz de descubrirlas. (Eugene Paul Wigner, 1963)

En nuestro planeta, es posible encontrar una infinidad de elementos relacionados al mundo de

las matemticas. Se han descubierto magnficas creaciones de la naturaleza, las cuales poseen

patrones tan perfectos, que refuerzan la tan ansiada pregunta: Fueron las matemticas

descubiertas o inventadas? La razn urea es un nmero algebraico irracional que puede ser

relacionado y encontrado enormemente en la naturaleza, la arquitectura, e incluso en las

dimensiones de nuestro cuerpo. Se lo puede identificar en el caparazn de la concha del caracol,

algunas hojas de rboles, y tambin en plantas como el girasol. Me parece un tema que logra

incentivar a las personas a contemplar y aprender sobre la perfeccin de este tipo de patrones

matemticos, y poder estimular a los jvenes a contemplar esta relacin entre matemtica y el

mundo real, y as disponerse a estudiar esta ciencia como una disciplina llena de misterios y

asombros.

Por esta razn, mi propsito para esta investigacin, es demostrar la subsistencia del nmero

ureo en la aclamada sucesin de Fibonacci y el rectngulo ureo, para as sustentar mis

resultados y declaraciones sobre la relacin de ambos conceptos en cuanto a monumentos

arquitectnicos, la naturaleza y el cuerpo humano.

1. Nmero ureo

El nmero ureo es tambin llamado proporcin o razn urea, e incluso el nmero de oro. Este

se representa con el smbolo , pronunciado como (Phi) en consideracin al escultor griego

Fidias. El nmero ureo corresponde a la ecuacin algebraica 1+ 5

2. Esta da como resultado el

nmero: 1.618033989 hasta el infinito.

La principal caracterstica de es que no puede ser expresado como una proporcin de los nmeros enteros, es decir, que es irracional. Tambin tiene un periodo infinito, ya que sus cifras

decimales nunca se repiten de manera peridica.

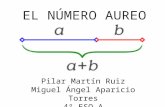
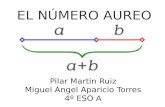
Se puede representar el nmero ureo mediante un segmento de recta:

Este segmento se divide en dos partes a y b, siendo a mayor que b. El nmero ureo siendo

geomtricamente identificado como una proporcin, conlleva a la existencia de una proporcin

urea si la razn entre la longitud de (a+b) y la longitud a en este segmento de recta, es igual a

la razn entre la longitud de a entre la menor longitud b.

+

=

Por consiguiente, es posible determinar una relacin algebraica:

( + ) = 2

2 = ( ) + 2

Entonces, es posible otorgarle a la grfica una variable x para despejar la ecuacin. La suma de

variables a+b se reemplaza por el nmero entero (1), y sus partes se distribuyen mediante la

variable (x) y (1-x). La grfica se representa de la siguiente manera:

Se resuelve la igualdad establecida de la siguiente manera:

+

1

1

=

1

1 = 2

2 + 1 = 0

Se logra obtener una ecuacin cuadrtica en la que aplicando el principio de la ecuacin de

segundo grado se obtiene:

= + 2 4

2

= 1 + 1 4(1)(1)

2

=1 + 5

2

Ahora para calcular la proporcin deseada se debe dividir el segmento mayor de la recta (x) entre

(x-1)

1 =

1 + 52

3 52

=1 + 5

3 5=

(1 + 5) (3 + 5)

(3 5) (3 + 5)

1 =

3 5 + 35 + 5

9 + 35 35 25=

2 + 25

9 5=

1 + 5

2= 1.6180339

1.1 Rectngulo ureo y su presencia en la arquitectura

.

En esta grfica, podemos observar un

cuadrado en el que sus lados tienen

una longitud de 2 unidades. El

segmento de recta posee una

longitud de 1, consecuentemente

dando como resultado una diagonal

de magnitud 5, ya que: =

12 + 22 = 5

De esta manera se traza una

circunferencia en la que el centro de

esta est localizada en B, y pase por el

punto A.

As se obtiene finalmente un

rectngulo, en la que se demuestra

que su proporcin (la proporcin es la

divisin del lado mayor como

numerador, y el menor como

denominador) satisfacen la ecuacin

definida anteriormente y otorga .

1 + 5

As se obtiene finalmente un rectngulo, en la

que se demuestra que su proporcin (la

proporcin es la divisin del lado mayor como

numerador, y el menor como denominador)

satisfacen la ecuacin definida anteriormente

y otorga .

2

Luego de trazar la circunferencia, se

crea un nuevo punto F. Este punto es el

resultado del trazado de una llnea recta

horizontal desde el punto D hasta que

toque un punto de dicha circunferencia.

Se traza, de igual manera, una lnea

recta vertical en F, y una recta

horizontal desde C. Entonces el punto

de interseccin entre ambas rectas

otorgar el nuevo y ltimo vrtice del

rectngulo. Este tendr como base 1 +

5 y como altura 2 unidades.

Un rectngulo ureo tiene la propiedad de ser dividido en un cuadrado, y el rectngulo resultante

tendr las mismas proporciones que el original.

Este nuevo rectngulo podr volver a realizar la misma accin, creando un infinito. El rectngulo

ureo es la representacin principal para la sucesin de Fibonacci, la cual veremos

posteriormente.

Esta medida urea del rectngulo es encontrada en antiguas construcciones arquitectnicas

griegas las cuales tienen, al mismo tiempo, una relacin estrecha con la sucesin de Fibonacci, la

cual va de la mano con el nmero ureo.

Figura 1. Rplica exacta del antiguo templo Partenn.

El templo Partenn, construido entre los aos 447 y 442 a.C. es una de las construcciones

arquitectnicas antiguas construida por los griegos. La parte frontal de esta estructura posee las

dimensiones pertenecientes al concepto de Phi. Su forma es de un rectngulo ureo, y en la

imagen tambin se relaciona con la espiral logartmica, presente en la sucesin de Fibonacci.

Esta otra figura muestra parte de la

estructura, donde se pueden

presenciar dos rectngulos ureos

localizados de manera vertical y

horizontal con respecto a su forma.

Esta imagen ilustra imagen ilustra las

proporciones proporcin urea que

aparecen en la altura de la viga de soporte

del techo y en las secciones rectangulares

decorativas que corren horizontalmente a

travs de l. Los cuadrados dibujados en la

imagen ayudan a visualizar los rectngulos ureos, que poseen una relacin entre la anchura y la altura

de exactamente 1,618 a 1.

Figura 2. Rectngulos ureos en la estructura del

Partenn.

1.2 Nmero ureo en la estructura humana

El nmero ureo, despus de todo, forma parte incluso de nuestras propias medidas. El cuerpo

humano posee proporciones varias de todo tipo, y en varias de ellas est presente .

Esta imagen proporciona todas las partes del cuerpo que

presentan proporcin urea, al dividir una medida con

otra. La primera corresponde a la divisin entre nuestra

altura total (h), entre la altura desde nuestra cabeza

hasta la punta de los dedos (a), con los brazos estirados

y pegados al cuerpo. Asimismo, al dividir (a) entre la

medida de la cabeza hasta el ombligo, dara como

resultado el nmero 1.618. Esta razn tan solo

resultara en mediciones pticas y no aplica para todos,

pero si para la mayora.

Longitudes en el cuerpo Medida obtenida (0.05 cm)

a 102

b 63

c 38

d 24

e 60

f 44

h 172

a = Desde la planta de los pie hasta el codo.

b = Desde el tope de la cabeza hasta el codo.

c = Distancia horizontal entre los hombros.

d = Desde el tope de la cabeza hasta la barbilla.

e = Desde los codos hasta las rodillas.

Para comprobar estas proporciones proced a medir

dichas partes de mi cuerpo usando un flexmetro de

error 0.05 cm, y as comprobar la exactitud de los

resultados en cuanto al nmero ureo.

Figura 3. Proporciones ureas en el

cuerpo humano.

Proporcin Resultado Error Error porcentual

a/b 1.619 0.001 0.06%

h/a 1.686 0.068 4.20%

b/c 1.658 0.04 2.47%

c/d 1.583 0.035 2.16%

e/f 1.364 0.254 15.70%

Resultado esperado 1.618

Segn esta grfica es posible determinar la exactitud de los datos con respecto al nmero ureo.

Claramente los datos muestran un claro indicio de la veracidad de la grfica del cuerpo humano,

que muestra longitudes predeterminadas y sus respectivas proporciones. Es importante recalcar

que estas proporciones no se van a cumplir en todos los casos, ya que la fisionoma humana es

muy diferente entre las personas.

El error ms bajo se dio en la divisin de la longitud a entre la b, siendo este de apenas un

0.06%, siendo este mayor en tan solo 0.001 centmetros; mientras que el error ms alto apareci

en la proporcin de e entre f, alcanzando casi el 16%. Sin embargo, en la mayora de los datos

hay un error casi despreciable, por lo que se pudo concluir que en mi propio cuerpo, s existe la

proporcin urea.

1.3 Nmero ureo y Sucesin de Fibonacci - Naturaleza

Leonardo de Pisa, matemtico de origen italiano, conocido como Fibonacci, fue el creador de la

Sucesin de Fibonacci, una sucesin numrica presente en la naturaleza y poseedora de

aplicaciones tiles en las matemticas y la informtica.

Es una sucesin infinita compuesta nicamente por nmeros naturales.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765...+

Esta sucesin se obtiene mediante la suma de los dos trminos anteriores, desde el tercer trmino. De

esta manera: 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5

f = Desde las rodillas hasta la planta de los pies.

Figuras 4 y 5. Sucesin de Fibonacci representada por rectngulos ureos.

La frmula de la sucesin es la siguiente:

= 1 + 2 para 3

Sin embargo, con esta frmula es necesario conocer toda la lista de la sucesin de Fibonacci, al menos si

el es un nmero muy grande.

Por esta razn, se utiliza Phi (Nmero ureo), en una nueva ecuacin en la que se podr tener como resultado un nmero de la sucesin de Fibonacci con respecto a un nmero .

= (1 )

5

Si se quiere encontrar un nmero en la sucesin de Fibonacci en una posicin , por ejemplo, la

posicin 20. Se calcula de la siguiente manera.

20 =20 (1 )20

5

20 =15126.99999 (0.618033989)20

2.236067977= 6765

Cabe recalcar que la relacin entre el nmero ureo y la sucesin de Fibonacci es an ms

estrecha, ya que la divisin de un trmino entre 1, da un nmero cercano a Phi. En otras

palabras, el lmite de estas divisiones infinitas es 1.618033989, y el producto en las divisiones

siempre oscila entre un lmite por la izquierda y por la derecha, representado de la siguiente

manera.

Esta figura muestra en el eje de las y una lnea continua, la cual represente el nmero ureo. En

el eje de las x se muestra las razones de

1, las cuales se acercan al lmite , pero nunca llegan

a igualar dicho nmero irracional.

lim

1

=1 + 5

2

Por consiguiente:

= lim

1

= 1 + 2

1= lim (1 +

21

) = 1 + 21

= 1 +1

= 1 +1

2 1 = 0

La ecuacin demuestra que el lmite entre la razn de

1 da como resultado el nmero ureo,

ya que se obtiene la misma ecuacin algebraica al calcular Phi usando el segmento de recta en la

primera demostracin.

Con los conceptos claros de proporcin o nmero ureo, as como la sucesin de Fibonacci, es

relativamente sencillo darse cuenta del patrn que siguen varios elementos existentes en la

naturaleza, ya sea numricamente, geomtricamente, o una combinacin de ambos.

0

0.5

1

1.5

2

2.5

Aparicin de Phi en la proporcin entre los nmeros de la sucesin de Fibonacci

Sucesin de Fibonacci

Lineal (Nmero ureo)

=

1

1

2

1

3

2

5

3 8

5

13

8

21

13

34

21

55

31

Esta imagen contiene una concha de Nautilus, animal

encontrado en el mar, el cual posee una estructura de espiral

equiangular. Es comnmente reconocido como uno de los

ms notables ejemplos de la secuencia de Fibonacci y en la

naturaleza. Se bosqueja en su cuerpo un rectngulo ureo,

que se divide en ms rectngulos ureos hasta llegar al origen

visible. Se usa una espiral logartmica

= log (

) utilizando puntos especficos de estos

rectngulos, y as formar dicha espiral. Llamada tambin

espiral dorada, se denomina as porque su razn de

crecimiento da como resultado al nmero ureo.

Figuras 6 y 7. Fibonacci en la naturaleza.

Conclusin

El nmero ureo es uno de las tantas majestuosidades que podemos encontrar en el mundo de

las matemticas. He comprobado que esta proporcin se encuentra tanto en la arquitectura,

como en la naturaleza, de la cual nuestro propio cuerpo est incluido. Este trabajo conllevo un

rpido estudio de lo que es un nmero algebraico irracional; as como la comprobacin del origen

de la ecuacin 1+5

2. Pude utilizar mis conocimientos en sucesiones y lmites, los cuales aprend

como parte del programa del Diploma del Bachillerato Internacional.

Se demostr que (Phi) estar mayoritariamente vinculado con la sucesin de Fibonacci, aunque

esta ltima tiene una completa relacin con la primera. El nmero ureo tiene grandes

aplicaciones para la geometra, ya que gran parte de figuras geomtricas fueron utilizadas para

estudiar este nmero. La precisin y exactitud de los datos, especialmente en las mediciones de

las proporciones entre partes de mi cuerpo, fueron excelentes. A pesar de haber tenido muy poco

conocimiento sobre lo que era este fenmeno, gracias a las clases de Teora del Conocimiento en

En las plantas de girasol, sus

semillas estn dispuestas por

espirales. Es posible observar

que tiene 21 espirales

apuntando a la izquierda, y 34

apuntando a la derecha. Ambos

son nmeros consecutivos de la

sucesin de Fibonacci, y la

razn de estos nos da un

estimado cercano a Phi ().

cuanto a las matemticas, me incentiv a realizar este trabajo y poder extender mi visin acerca

de esta ciencia muy misteriosa pero fenomenal.

Bibliografa

Nmero ureo, (s.f). En Wikipedia. Recuperado el 1 de julio del 2015 de https://es.wikipedia.org/wiki/Nmero_ureo

Galaviz, J. (n.d.). Rectngulo ureo. Retrieved July 1, 2015, from

http://arquimedes.matem.unam.mx/PUEMAC/PUEMAC_2008/aurea/html/rectangulo.html

Golden Ratio in Geometry. (n.d.). Retrieved July 1, 2015, from http://www.cut-the-

knot.org/do_you_know/GoldenRatio.shtml

Rodriguez, M. (n.d.). El nmero de oro es irracional. Retrieved July 1, 2015, from

http://www.mecd.gob.es/eslovaquia/dms/consejerias-

exteriores/eslovaquia/publicaciones/material-did-ctico/numero-de-oro-recursos-didacticos.pdf

Toledo, Y. (n.d.). Seccin Aurea en Arte, Arquitectura y Msica. Retrieved July 1, 2015, from

http://matematicas.uclm.es/ita-cr/web_matematicas/trabajos/240/La_seccion_aurea_en arte.pdf

Snchez, C. (n.d.). Del nmero ureo a la sucesin de Fibonacci. Una curiosa relacin. Retrieved

July 2, 2015, from http://casanchi.com/mat/numeroaureo01.pdf

Ignacio, F. (n.d.). EL NMERO DE ORO. Retrieved July 2, 2015, from

http://rt000z8y.eresmas.net/El numero de oro.htm

Garca, A. (n.d.). Sucesin de Fibonacci. Retrieved July 2, 2015, from

http://cerezo.pntic.mec.es/~agarc170/paginas/fibonacci.htm

La sucesin de Fibonacci. (n.d.). Retrieved July 2, 2015, from

http://www.disfrutalasmatematicas.com/numeros/fibonacci-sucesion.html

Nautilus pompilius. (n.d.). Retrieved July 2, 2015, from

https://es.wikipedia.org/wiki/Nautilus_pompilius

Nmero ureo. (n.d.). Retrieved July 2, 2015, from http://aureo.webgarden.es/menu/naturaleza

El numero phi en las plantas. (n.d.). Retrieved July 2, 2015, from

http://www.castor.es/phi_plantas.html

Imgenes

[Imagen del Partenn bosquejado segn rectngulo ureo]. Recuperado de

http://www.susanabarriga.com.es/la-seccion-o-zona-aurea/

[Imagen de una concha de Nautilus]. Recuperado de

http://mathforum.org/mathimages/index.php/Fibonacci_Numbers

[Representacin grfica de la sucesin e Fibonacci]. Recuperado de

http://curiosidades.batanga.com/4461/que-es-la-sucesion-de-fibonacci

[Sucesin de Fibonacci representado en rectngulos ureos] (2012) Recuperado de

http://www.hydrogen2oxygen.net/en/the-fibonacci-sequence-is-the-mathematical-first-

cousin-of-the-golden-ratio/

Meisner, G. (2013) [Rectngulos ureos en la estructura del Partenn]

http://www.goldennumber.net/parthenon-phi-golden-ratio/