3º ESO Tema 7

1

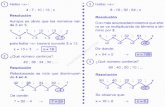
TEMA 7. SUCESIONES NUMÉRICAS.

1. SUCESIONES NUMÉRICAS. Imaginemos el recorrido que efectúa un balón que se ha lanzado al suelo y midamos las distancias entre bote y bote:

Las distancias forman una sucesión de números: 40, 35, 30, 25, ….

Una SUCESIÓN NUMÉRICA es un conjunto ordenado de números, que se llaman TÉRMINOS de la sucesión.

Cada término se representa por una letra y un subíndice que indica el lugar que ocupa dentro de ella.

En nuestro ejemplo, tenemos:

,401 =a .....,25,30,35 432 === aaa

Aquí, la distancia recorrida en cada bote es 5 cm. menor que la anterior. Podemos calcular así más términos de la sucesión: 40, 35, 30, 25, 20, 15, …

Esta sucesión tiene un número finito de términos. Se dice que es una SUCESIÓN FINITA.

Las que tienen infinitos términos se dicen SUCESIONES INFINITAS.

Un ejemplo de una sucesión infinita sería la formada por los cuadrados perfectos:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, …..

EJERCICIO 1. Escribe los 10 primeros términos de las sucesiones formadas por:

a) Los números pares : 2, 4, 6, 8, 10, 12, 14, 16, 18, 20

b) La suma de cada natural y su cuadrado: 2, 6, 12, 20, 30, 42, 56, 72, 90, 110

EJERCICIO 2. Completa los términos que faltan en las siguientes sucesiones:

a) 11, 14, 17, 20, 23, 26, 29, 32 c) 1, 3, 6, 10,15, 21, 28, 36 , 45, 55

b) 105, 100, 95, 90, 85, 80, 75, 70 d) 1, 8, 27, 64, 125, 216

2. TÉRMINO GENERAL DE UNA SUCESIÓN.

El TÉRMINO GENERAL ( ó TÉRMINO n-ÉSIMO ) , na , de una sucesión es una fórmula que nos permite

calcular cualquier término de la sucesión en función del lugar que ocupa.

Por ejemplo, en la sucesión de los cuadrados perfectos, cada término se obtiene elevando al cuadrado el

lugar que ocupa en ella:

,1121 ==a .....,164,93,42 2

4

2

3

2

2 ====== aaa

En esta sucesión, el término general será: 2nan =

3º ESO Tema 7

2

3. CÁLCULO DEL TÉRMINO GENERAL DE UNA SUCESIÓN. Dados los términos de una sucesión, para calcular su término general tenemos que buscar una regla que relacione el valor de cada término con el lugar que ocupa en la sucesión. Para hallar esta relación debemos descomponer los términos en expresiones numéricas que tengan la misma estructura dependiendo del lugar que ocupan.

EJEMPLO:

Consideremos la siguiente sucesión: 2, 5, 10, 17, 26, 37…..

Para calcular el término general nos ayudamos de la siguiente tabla:

Una vez que tenemos el término general, podemos calcular cualquier término de la sucesión, por ejemplo:

=10a 102+1=100+1=101

A veces no es posible obtener una fórmula para el término general, y otras veces no se consigue de forma inmediata.

EJERCICIO 3. A partir del término general, calcula los 4 primeros términos y el término centésimo de cada una de estas sucesiones:

a) 20+= nan c) 1

1

+

−=n

ncn e)

1

12

+=n

en

b) 42+= nbn d)

1

1.)1(

+−=

nd n

n f) 1

12

2

+

−=n

nf n

EJERCICIO 4. Calcula el término general de las siguientes sucesiones:

a) 11, 13, 15, 17, 19, 21, …: an=2n+9 e) 4, 9, 16, 25, 36, 49, 64, ….: an=(n+1)2

b) 1, 8, 27, 64, 125, … : an=n3 f) 10, 12, 14, 16, 18, 20, …..: an=2n+8

4. SUCESIONES RECURRENTES. Una SUCESIÓN es RECURRENTE cuando todos sus términos se pueden calcular a partir de uno dado.

La fórmula mediante la cual se pueden calcular los términos se llama LEY DE RECURRENCIA.

EJEMPLO: naa nn +=−1

Si sólo nos dan esta fórmula no podemos hacer nada. Pero si se añade el dato: 41 =a , entonces ya

podemos obtener el resto de los términos de la sucesión:

.....,9363,6242 2312 =+=+==+=+= aaaa

La ley de recurrencia sería: 41 =a ; naa nn +=−1

LUGAR 1 2 3 4 5 6 …. n …

TÉRMINO 2=12+1 5=22+1 10=32+1 17=42+1 26=52+1 37=62+1 …. n2+1 …

3º ESO Tema 7

3

5. PROGRESIONES ARITMÉTICAS. Una PROGRESIÓN ARITMÉTICA es una sucesión recurrente en la que cada término, a excepción del primero, se obtiene sumando al anterior un mismo número, d, que se llama DIFERENCIA DE LA PROGRESIÓN.

EJEMPLO:

1,3,5,7….. 11 =a ; 21 +=−nn aa

2, 6, 10, 14, 18, …… 21 =a ; 41 +=−nn aa

6. TÉRMINO GENERAL DE UNA PROGRESIÓN ARITMÉTICA.

Vamos a calcular el término general del 2º ejemplo, donde 21 =a y 4=d , y a partir de él determinar el de

una progresión aritmética cualquiera:

ejemplo caso general

244424).1(2

........

144.3244.22410

104.2244246

642

2

4

3

2

1

−=−+=−+=

=+=++=+=

=+=++=+=

=+=

=

nnna

a

a

a

a

n

dnaa

daddadaa

daddadaa

daa

a

n ).1(

........

32

2

1

1134

1123

12

1

−+=

+=++=+=

+=++=+=

+=

El TÉRMINO GENERAL de una PROGRESIÓN ARITMÉTICA que tiene como primer término 1a y como

diferencia d , se obtiene mediante la siguiente fórmula:

dnaan ).1(1 −+=

EJEMPLO:

11 =a ; 122212).1(12 −=−+=−+=⇒= nnnad n

7. SUMA DE LOS n PRIMEROS TÉRMINOS DE UNA PROGRESIÓN ARITMÉTICA. Voy a considerar la progresión aritmética: 2, 4, 6, 8, 10, 12, ….

La suma de sus 6 primeros términos se puede expresar de 2 formas:

Colocando una expresión sobre la otra y sumando ambas expresiones se tiene:

3º ESO Tema 7

4

De donde se obtiene:

422

848414.62 ==⇒== SS

Este proceso se puede generalizar para calcular la suma, nS , de los primeros n términos de una progresión

aritmética cualquiera:

Al igual que en el ejemplo anterior, todos los sumandos son iguales, y por tanto:

( )( )

2.2 1

1

nnnn

aanSaanS

+⋅=⇒+=⋅

La SUMA de los n primeros términos de una progresión aritmética de término general na es:

( )

2

1 nn

aanS

+⋅=

EJEMPLO:

� Suma de los 50 primeros números pares: ( )

25502

102.50

2

10025050 ==

+⋅=S

� Suma de los 20 primeros términos de la sucesión 51 =a y 6=d :

1191120120.6166656).1(5 20 =−=−=⇒−=−+=−+= annnan

( )1240

2

124.20

2

11952020 ==

+⋅=S

8. PROGRESIONES GEOMÉTRICAS. Una PROGRESIÓN GEOMÉTRICA es una sucesión recurrente en la que cada término, a excepción del primero, se obtiene multiplicando el anterior por un mismo número, r , que se llama RAZÓN DE LA PROGRESIÓN.

EJEMPLO:

2, 6, 18, 54, 162,…… 21 =a ; 31 ⋅=−nn aa

1, 4, 16, 64, 256, …… 11 =a ; 41 ⋅=−nn aa

Se puede calcular la razón de la progresión dividiendo un término entre el anterior. De la misma forma, para comprobar si una sucesión es una progresión geométrica, basta con dividir cada término entre el anterior y comprobar si se obtiene el mismo valor:

13

4

2

3

1

2 ......−

=====n

n

a

a

a

a

a

a

a

ar

3º ESO Tema 7

5

9. TÉRMINO GENERAL DE UNA PROGRESIÓN GEOMÉTRICA.

Vamos a calcular el término general del 2º ejemplo, donde 11 =a y 4=r , y a partir de él determinar el

de una progresión geométrica cualquiera:

ejemplo caso general

1

32

4

2

3

2

1

41

........

6441441416

164144144

441

1

−⋅=

=⋅=⋅⋅=⋅=

=⋅=⋅⋅=⋅=

=⋅=

=

n

na

a

a

a

a

1

1

3

1

2

134

2

1123

12

1

........

−⋅=

⋅=⋅⋅=⋅=

⋅=⋅⋅=⋅=

⋅=

n

n raa

rarraraa

rarraraa

raa

a

El TÉRMINO GENERAL de una PROGRESIÓN GEOMÉTRICA que tiene como primer término 1a y

como razón r , se obtiene mediante la siguiente fórmula:

1

1

−⋅=

n

n raa

EJEMPLO:

31 =a y 3=r nnn

na 3333 111==⋅=⇒

−+−

10. SUMA DE LOS n PRIMEROS TÉRMINOS DE UNA PROGRESIÓN GEOMÉTRICA.

Voy a considerar la P.G. dada por 31 =a y 2=r : 3, 6, 12, 24, 48, 96, 192, ….

La suma de sus 7 primeros términos es:

Multiplicamos esta expresión por la razón 2, y a ella le restamos esta igualdad:

Despejamos la suma en esta última igualdad y se obtiene:

3º ESO Tema 7

6

Este proceso se puede generalizar para calcular la suma, nS , de los primeros n términos de una

progresión geométrica cualquiera:

Al igual que en el ejemplo, se extrae factor común y se despeja:

La SUMA de los n primeros términos de una progresión geométrica de término general na es:

1

1

−

−⋅=

r

aarS nn

EJEMPLO. Suma de los 6 primeros términos de la PG dada por 11 =a y 2=r :

323212 16

16 =⋅=⋅=−aa

631641

1322

12

2 166 =−=

−⋅=

−

−⋅=

aaS

11.