UNIVERSIDAD NACIONAL DE PIURA

EJEMPLO- VIGA EMPOTRADA.

Una viga de longitud est empotrada en ambos extremos. Determine la desviacin de esa viga si sostiene una carga constante, , uniformemente distribuida en su longitud; esto es , .

Solucin

Segn lo que acabamos de plantear; la desviacin satisface a

Dado que la viga est empotrada en su extremo izquierdo () y en su extremo derecho , no hay desviacin vertical y la elstica es horizontal e esos puntos. De esta manera las condiciones en la frontera son:

Podemos resolver determinando teniendo en cuenta que es una raz de multiplicidad cuatro de la ecuacin auxiliar , luego determinamos una solucin particular por el mtodo de coeficientes indeterminados. Tambin podemos resolver integrando cuatro la ecuacin:

Se obtiene como solucin general:

Con las condiciones se obtiene ,

Sin embargo las otras condiciones restantes aplicados a la ecuacin:

Dan origen a:

Resolviendo el sistema se obtiene:

|En consecuencia la desviacin es:

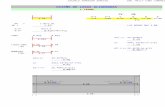
Si , se obtiene la grfica de la curva elstica de la figura 14

Figura 14Ejemplo: De Problema Relacionado Con Valores Propios.

Determinar la desviacin de una columna homognea, delgada y vertical de altura , sometida a una carga axial constante. La columna se encuentra articulada en sus dos extremos.

Solucin.El problema de valor en la frontera que se debe resolver es:

es una solucin valida para este problema, lo que indica que si la carga no es suficientemente grande, entonces no hay deflexin. Luego para qu valores de se curva la columna?. En trmino matemticos: para qu valores de el problema de valor en la frontera tiene soluciones no triviales?

Haciendo la sustitucin se obtiene:

Es idntica al problema de soluciones no triviales de un problema de valor en la frontera, en el caso III de este problema se observa que las curvas de desviacin son: , que corresponden a los valores propios

Esto quiere decir fsicamente, que la columna se desva slo cuando la fuerza de compresin tiene uno de los valores Estas fuerzas se llaman cargas crticas. La curva de deflexin que corresponde a la mnima carga crtica, se denomina carga de Euler y es ; esta funcin se conoce como primer modo de desviacin.

En la siguiente figura vemos las curvas de desviacin del presente ejemplo, que corresponden para . Si la columna original tiene algn tipo de restriccin fsica o gua en , la carga crtica mnima ser , y la curva de deflexin ser la de la figura(b). Si ponen guas a las columnas en y en , la columna no se desviar sino hasta aplicarle la carga crtica y la curva de desviacin ser la que se ilustra en la figura (c) . Dnde se deberan poner guas en la columna para que la carga de Euler sea ?

Figura 163