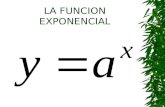1.3.4 Ejercicios resueltos sobre la función exponencial y logarítmica 1. Use las propiedades de la función exponencial (teorema 1) para simplificar totalmente la siguiente expresión: ( )

( )( )

( )( )

( )xx

xx

x

xx

xx

x

21

12

32

1

1

22

35

33

3

5225

552

2

−

+−

+⋅

÷÷

⋅

÷

Solución. ( )

( )( )

( )( )

( ) 2

2

2

2

2

2

2

2

2

26

22

4

21

12

32

1

1

22

35

333

55355

35

33

3

5225

55xx

xx

xx

x

x

x

xx

xx

x

xx

xx

x

−

+

−−

+−

+⋅

÷⋅

⋅⋅

÷=⋅

÷÷

⋅

÷

222

222

222

264

3353535

xxxxxx

xxxx

−−++

+−−

⋅⋅⋅

⋅⋅=

22

22

222

222

22

64

222

624

3535

5335

xxx

xxx

xxxxxx

xxxx

−++

−++

++−+−+

−++−

⋅

⋅=

⋅

⋅=

( ) ( ) 20253535 422624 2222

=⋅=⋅= −−−++−++ xxxxxx

2. Pruebe que ( ) ( )

( )1

2

122

2

22

+=

+−

−⋅+

−−+

−

−−

−−

x

x

xx

xxxx

xxxx

ee

eeeeee

eeee

Solución. Simplifique inicialmente el numerador y el denominador de la fracción. Así: ( ) ( ) 422 222222

=−+−++=−−+ −−−− xxxxxxxx eeeeeeee También,

( ) ( )( )

( ) ( )xxxx

xx

xxxx

xx

eeee

eeee

eeeeee

−−

−

−−

−−

+⋅+=

+⋅+=

+−

−⋅+241 2

2

22

2

( )xx ee −+= 2

En consecuencia,

( ) ( )

( )( ) 1

21

22

4

122

2

22

+=

+=

+=

+−

−⋅+

−−+−

−

−−

−−

x

x

xx

xx

xx

xxxx

xxxx

ee

eeee

eeeeee

eeee

3. Es posible medir la concentración de alcohol en la sangre de una persona. Investigaciones médicas recientes sugieren que el riesgo R (dado como porcentaje) de tener un accidente automovilístico puede ser modelado mediante la ecuación:

kxeR 6= (1)

donde x: es la concentración de alcohol en la sangre y k una constante. a) Al suponer una concentración de 0.04 de alcohol en la sangre produce un riesgo del

10% (R = 10) de sufrir un accidente, ¿cuál es el valor de la constante?. b) Utilice el valor de k e indique cuál es el riesgo para diferentes concentraciones de

alcohol (0.17, 0.19, ...). c) Con el mismo valor de k indique la concentración de alcohol correspondiente a un

riesgo del 100%. d) Si la ley establece que las personas con un riesgo del 20% o mayor de sufrir un

accidente no deben conducir vehículos ¿con cuál concentración de alcohol en la sangre debe un conductor ser arrestado y multado?.

Solución. a) Una concentración de4 0.04 y un riesgo del 10%, indica que x = 0.04 y R = 10. Al

sustituir estos valores en la ecuación (1) se obtiene: 10 ke 04.06=

ke 04.0

610

=

ke 04.06

10=log (Definición del logaritmo)

77.126

10ln04.01

==k

Con el valor de k encontrado, la ecuación (1) se puede escribir en la forma:

xeR 77.126= (2) b) Al sustituir en la ecuación (2), se obtiene: 17.0=x 6.526 17.077.12 == ×eR Este resultado indica que para una concentración de alcohol de 0.17, el riesgo de sufrir un accidente es del 52.6%. c) Al sustituir R = 100 en la ecuación (2) y solucionando para x se obtiene: 100 xe 77.126=

xe 77.12

6100

=

xe 77.126

100=log (Definición del logaritmo)

22.06

100ln77.12

1==x

Lo que indica que para una concentración de alcohol de 0.22, el riesgo de sufrir un accidente es del 100%. d) Con R = 20 en la ecuación (2), se determina la concentración x de alcohol en la

sangre: xe 77.12620 =

xe 77.12

620

=

094.0620ln

77.121

==x

Este resultado indica que un conductor que presente una concentración de alcohol mayor o igual a 0.094 debe ser arrestado y multado. 4. Una colonia de bacterias crece de acuerdo con la ley de crecimiento no inhibido. Si la

cantidad de bacterias se duplica en tres horas; cuánto tiempo tardará la colonia en triplicar su número?

Solución. Recuerde inicialmente que el número N de células en un instante t es:

kteNtN 0)( = (1)

donde : es la cantidad inicial de bacterias presentes y k es una constante positiva. 0N

La afirmación: la cantidad de bacterias se duplica en 3 horas, significa que: . 02)3( NN = Pero de acuerdo a (1), keNN 3

0)3( = Así que: keNNN 3

002)3( == Luego, 2ln323 =⇔= ke k

De donde 231.02ln31

≈=k

Con dicho valor de k, la fórmula (1) se transforma en: (2) teNtN 231.0

0)( = Ahora, el tiempo t necesario para que el tamaño de la colonia se triplique necesita que

. Sustituyendo en (2) y resolviendo para t se obtiene: 03NN =

teNN 231.0003 =

De donde, 756.43ln231.01

≈=t horas. Se necesitan 4.756 horas para que el tamaño se

triplique. 5. Use la definición de logaritmos para cambiar cada expresión exponencial en una

logarítmica en los siguientes casos: a) 16 b) 24= π=2x c) 8=e x

Solución. a) 16 216log4 4

2 =⇔= b) 2log2 =⇔= ππ xx c) e xx =⇔= 8ln8 6. Use la definición de logaritmos para cambiar cada expresión logarítmica en una

exponencial equivalente en los siguientes casos:

a) log b) log382 = 3=xπ c) 4ln =x Solución. a) log 8238 3

2 =⇔= b) log xx =⇔= 33 ππ

c) ln xexx e =⇔=⇔= 44log4 7. Pruebe que si a > 0, y x > 0, entonces, 1≠a xxa

21loglog −= .

Solución. Suponga que (1). Esto significa, de acuerdo a la definición, que (2).

yxa =log yax =

De (2), se deduce que y

y aax

==111 . Pero, ( ) yxax

y

=⇔

= 1log11

21 (3).

De (1) y (3), se concluye que:

( ) xxxxaaaa

a 1111 loglog1log1loglog −=−==

8. Sea a > 0, x > 0 y, además, Solución. Si ( ) , entonces, ( ) 057 5log7log =− aa xx ( ) ( ) 5log7log 57 aa xx = . Tomando logaritmo en base a, en ambos miembros de la última igualdad, se obtiene:

( )[ ] ( )[ ]57 5log7lo aa Loga

Loga xxg = . O equivalentemente,

( ) ( )xx aaaaaa log5log5loglog7log7log +⋅=+⋅ Despejando y simplificando, se obtiene: xalog

( ) ( ) ( )( )351log35log

5log7log7log5log7log5log

5log7log7log5log

log22

aaaa

aaaa

aa

aaa x =−=

−+−

=−−

=

En consecuencia, 351

=x .

9. Determine los valores de x e y que satisfacen simultáneamente las ecuaciones: (1) 1010=⋅ yx (2) 25log 10=xy Solución. De la ecuación (2), se sigue que x e y son reales positivos. Además, se puede deducir que:

25loglog =⋅ yx (3). De donde, y

xlog

25log = (4).

Como x, y son reales positivos, se sigue de (1) que log 10log =+ yx (5). De (4) y (5), se deduce que:

0)5(log025)(log10)(log10loglog

25 22 =−⇔=+−⇔=+ yyyyy

De donde, . 5105log =⇔= yy Sustituyendo el valor de y en la ecuación (1), se obtiene . 510=x 10. ¿Cuál es la magnitud de un terremoto cuya lectura sismográfica es de 0.1 milímetros a

una distancia de 100 kilómetros del epicentro? Solución. De acuerdo a la fórmula (3) de la sección 1.3.3.2, si 1.0=x , entonces la magnitud

de este terremoto es: )(xM

210log1010log

001.01.0loglog)1.0( 2

3

1

0

==

=

=

=

−

−

xxM

Lo que indica que el terremoto mide 2.0 en la escala de Richter.

11. El devastador terremoto de San Francisco en 1906 midió 8.9 en la escala de Richter.

¿Cómo se compara este terremoto con el de Papúa, Nueva Guinea, en 1988, que midió 6.7 en la escala de Richter?

Solución. Si , denotan respectivamente, las lecturas sismográficas de los terremotos de San Francisco y Papúa, se tiene entonces de acuerdo a la fórmula (3) de la sección 1.3.3.2:

1x 2x

=

=

0

2

0

1 log7.6;log9.8xx

xx

Pero:

9.8

0

1

0

1 109.8log =⇔=

xx

xx

(1)

7.6

0

2

0

2 107.6log =⇔=

xx

xx

(2)

La relación (1) indica que el terremoto de San Francisco fue 10 mas intenso que uno de nivel cero.

9.8

Igualmente, la relación (1) indica que el terremoto de Papúa fue 10 mas intenso que uno de nivel cero.

7.6

Ahora, la relación: 15810101010 2.27.69.8

07.6

09.8

2

1 ≈==××

= −

xx

xx

O equivalentemente: , indica que el terremoto de San Francisco fue 158 veces mas intenso que el terremoto de Papúa.

21 158xx ≈