Geometría Analítica.....Unidad 2

Unidad 2 Lugares GeométricosSección 2.5 Elipse

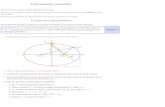
Se llama Elipse al lugar geométrico de los puntos P(x, y) tal que la suma de sus distancias a dos puntos fijos, llamados focos, es una constante.

Para un punto P(x, y) cualquiera de la elipse la suma de sus distancias a los focos es 2a es decir:

que se reduce a

(a2 – c2)(x – h)2 + a2(y – k)2 = a2(a2 – c2)……..(1)

De la figura deducimos lo siguiente , por definición

de elipse

, sustituyendo en (1) queda:

b2(x – h)2 + a2(y – k)2 = a2b2

Ecuación de la elipse cuando el eje mayor es paralelo al eje X, con centro C(h,k) y cuyos ejes mayor y menor tienen longitudes 2a y 2b respectivamente, en el caso de que el eje mayor sea paralelo al eje Y la ecuación de la elipse es:

En el caso que el centro C de la elipse este en el origen del plano coordenado h=0 y k = 0 quedando las ecuaciones de la elipse de la forma siguiente:

FJDM…..004D…..010D…..014D…..7

Geometría Analítica.....Unidad 2

(Eje mayor coincide con el eje X)

(Eje mayor coincide con el eje Y)Lado recto: es la longitud de la recta perpendicular al eje mayor y que pasa por los focos

Longitud del lado recto =

Excentricidad que se representa con la letra e, se define como el cociente de la semidistancia focal c entre el semieje mayor a, por lo cual podemos expresarla

como: e = . Si e = 0 implica que c = 0, de la formula a2 – c2 = b2 tenemos que a

= b, en cuyo caso la curva es una circunferencia, la que puede ser considerada como un caso especial de la elipse con excentricidad nula. Si e = 1 es evidente que a = c, de la formula a2 – c2 = b2 resulta que b = 0, en cuyo caso la deformación ha sido total, convirtiéndose la curva en una línea recta, en consecuencia .

Ejemplos: 1. Determinar la longitud del eje mayor y del eje menor, las coordenadas de los focos (F y F’) y de los vértices (V, V’, B, B’) de la elipse con centro en el origen, dada por la ecuación: 9x2 + 16y2 = 144Solución: Dividimos ambos miembros de la ecuación por 144 y simplificamos

Se trata de una elipse horizontal ya que denominador de x es mayor que el denominador de Y, sus vértices son: V(4,0), V’(-4,0) y B(0,3), B’(0, -3) longitud del Eje mayor = 2a = 8, Longitud del Eje menor = 2b = 6.Se sabe que b2 = a2 – c2 c2 = a2 – b2 c2 = 16 – 9 c siendo las coordenadas de los focos F( ,0) y F’( ,0).

FJDM…..004D…..010D…..014D…..7

Geometría Analítica.....Unidad 2

2. Una elipse tiene su centro en el origen y su eje mayor coincide con el eje Y, si uno de sus focos es el punto F(0,3) y la excentricidad es ½ , hallar las coordenadas del otro foco F’, las longitudes del eje mayor y menor, la ecuación de la elipse y la longitud de sus lados rectos.

Solución:

Como uno de los focos es F(0,3) tenemos que c = 3 otro foco será F’(0,-3), por

otro lado se nos indica que e = ½ = , tenemos también que:

b2 = a2 – c2 = 36 – 9 , por tanto la longitud del eje mayor es 2a = 12 la del eje menor = 2b = . La longitud de lado recto =

, como el eje de la elipse es vertical y su centro esta en el

origen la ecuación de la elipse es , la ecuación

de la elipse es: Adicionalmente calcularemos los vértices de esta elipse, como a = 6 y b = Tenemos que V(0,6), V’(0,-6) y B( ,0) , B’(- ,0). Una grafica de esta elipse seria:

FJDM…..004D…..010D…..014D…..7

Geometría Analítica.....Unidad 2

3. Determinar la ecuación de la elipse que tiene por vértices V(10,6), V’(-10,6) y la longitud del lado recto es 10.

Solución: el centro de esta elipse es de coordenadas C(h,k) y no coincide con el origen, además es el punto medio del segmento , por lo que las coordenadas del centro serán C(0,6) y a = 10, el eje mayor es horizontal, por lo que la forma de la ecuación esta dada por:

En esta ecuación conocemos a y las coordenadas del centro h y k, nos falta conocer b, la cual determinaremos usando la longitud del lado recto que nos dan, entonces tenemos:

LR = , finalmente sustituyendo en la ecuación

de la elipse tenemos:

, que es la ecuación de la elipse buscada.

Ecuación general de la elipse:

Tomemos la ecuación de la elipse cuyo centro no es el origen y su eje mayor es paralelo a eje X.

Desarrollando:

Si A = b2, C = a2, D = -2b2h, E = -2a2k, F = b2h2 + a2k2 – a2b2. nos queda que la ecuación general de la elipse es:

Ax2 + Cy2 + Dx + Ey + F = 0

Si tomamos la ecuación de la elipse cuyo centro no es el origen su eje mayor es paralelo al eje Y tenemos que A = a2, C = b2, D = -2a2h, E = -2b2k, y F = a2h2 + b2k2 – a2b2.

Reducción de la ecuación general de la elipse a la ecuación ordinaria:

FJDM…..004D…..010D…..014D…..7

Geometría Analítica.....Unidad 2

Dada una ecuación del tipo Ax2 + Cy2 + Dx + Ey + F = 0 esta puede

transformarse en otra del tipo: , haremos u ejemplo para demostrar el proceso:

4. Reducir la ecuación 4x2 + 9y2 – 8x + 18y – 23 = 0 a la ecuación ordinaria.Solución:

Agrupamos términos en x e y:

4x2 – 8x + 9y2 + 18y – 23 = 0 y completamos cuadrados,

4(x2 – 2x + 1 – 1) + 9(y2 + 2y+ 1 – 1) – 23 = 0

4((x – 1)2 – 1 )+ 9((y – 1)2 – 1) = 23 4(x – 1)2 + 9(y + 1)2 = 23 + 4 + 9

4(x – 1)2 + 9(y + 1)2 = 36, dividiendo entre 36 queda:

Esta es una elipse de centro C(1, -1), de la ecuación tenemos que a = 3 y b = 2 determinamos c, así, c2 = a2 – b2 = 9 – 4 = 5 c = , los focos son F(1+ , -1) y F’(1- , -1), los vértices se obtienen sumando y restando a la coordenadas del centro los semiejes de las elipses V(1+3, -1) y V’(1-3, -1), lo que resulta V(4, -1) y V’(-2, -1), B(1, -1 + 2), B’(1, -1 – 2), lo que resulta B(1, 1) y B(1, -3). Su lado

recto es LR = .

Lo anterior lo podemos demostrar de la siguiente manera partiendo de

Ax2 + Cy2 + Dx + Ey + F = 0 completando cuadrados obtenemos:

Sea M = , si M la ecuación anterior puede escribirse así:

, que es la ecuación ordinaria de la elipse. Si

es mayor que cero la ecuación anterior representa una elipse, si es igual a cero la elipse se reduce a un punto, si es menor que cero es imaginaria por lo que la ecuación no representa ningún lugar geométrico.

FJDM…..004D…..010D…..014D…..7

Geometría Analítica.....Unidad 2

5. Reducir a la ecuación ordinaria la elipse x2 + 3y2 – 8x – 12y + 32 = 0.Solución:

Agrupamos términos en x e y: x2 – 8x + 3y2 – 12y + 32 = 0 y completamos cuadrados:

(x2 – 8x + 16 – 16) + 3(y2 – 4y + 4 – 4) + 32 = 0

(x – 4)2 – 16 + 3((y – 2)2 – 4) + 32 = 0 (x – 4)2 + 3(y – 2)2 + 32 – 16 – 12 = 0

(x – 4)2 + 3(y – 2)2 = - 4

Aquí el valor de M es menor que cero por lo cual esta elipse no existe es imaginaria.

Problemas para resolver:I. Hallar el centro, los focos, los vértices, la excentricidad, la longitud del lado recto y las longitudes de cada eje de cada una de las elipses siguientes:

a) b)

c) d) x2 + 4y2 = 4

e) 3x2 + 2y2 = 6 f) 4x2 + y2 = 1

g) h) 225x2 +289y2 = 65025 *

II. Hallar las ecuaciones de las elipses siguientes de forma que satisfagan las condiciones que se establecen:

a) Centro C(0,0); Foco F(2,0) y vértice V(3,0).b) Vértices V(5,0), V’(-5,0), excentricidad 3/5.c) Vértices V(0,2), V’(4,2), eje menor con longitud 2.d) Focos F(0,5), F’(0, -5); suma de distancia a los focos de un punto

cualquiera de la elipse igual a 14.e) Longitud del lado recto = 5, vértices V(10,0), V(-10,0). *f) Focos F(5,0), F’(-5,0), excentricidad = 5/8. *

g) Centro origen, uno de sus vértices (0, -7) y pasa por el punto P **

h) Centro en el origen, su eje menor coincide con el eje X y la longitud de su eje mayor es el doble de la de su eje menor. **

FJDM…..004D…..010D…..014D…..7

Geometría Analítica.....Unidad 2

i) Centro en el origen, eje mayor sobre el eje X y que pasa por los puntos A(4,3) y B(6,2). *

j) Hallar la ecuación de la elipse que pasa por los puntos A(-6,4), B(-8,1), C(2,-4) y D(8,-3) y cuyos ejes son paralelos a los ejes de coordenadas. *

k) Hallar la ecuación de la elipse que pasa por los puntos A(0,1), B(1,-1), C(2,2) y D(4,0) y cuyos ejes son paralelos a los ejes de coordenadas. *

l) Hallar la ecuación de la elipse que pasa por los puntos A(1,3), B(-1,4),

C(0,3– ) y D(-3,3) y cuyos ejes son paralelos a los ejes de

coordenadas. **Nota: para los problemas de esta sección J, K, L asuma la siguiente ecuación de la elipse x2 + Cy2 + Dx + Ey + F = 0.

III. En cada uno de los siguientes ejercicios reducir la ecuación dada a la forma ordinaria de la ecuación de la elipse y determínese el centro, vértices y focos, las longitudes de los ejes mayor y menor, la del lado recto y la excentricidad.

a) 9x2 + 4y2 + 36x – 24y + 36 = 0b) 16x2 + 25y2 + 50y – 32x + 31 = 0c) 12x2 + 20y2 + 40y – 12x – 37 = 0d) x2 + 4y2 + 16y – 6x + 21 = 0e) 4x2 + 9y2 + 32x – 18y + 37 = 0f) 9x2 + 4y2 – 8y – 32 = 0

IV. Hallar el lugar geométrico de los puntos P(x,y) cuya suma de distancia a los puntos fijos A(2,-3) y B(2,7) sea igual a 12. *

V. Hallar el lugar geométrico de los puntos P(x,y) cuya suma de distancia a los puntos fijos A(3,1) y B(-5,1) sea igual a 10. *

VI. Hallar el lugar geométrico de los puntos P(x,y) cuya distancia al punto fijo A(3,2) sea la mitad de la correspondiente a la recta x + 2 = 0. *

FJDM…..004D…..010D…..014D…..7