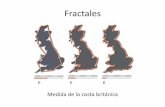
Fractales
-
Upload
gregoriofernandez -
Category
Documents
-
view
225 -
download
1
description
Transcript of Fractales
Colegio La Casa de CartnGoyo Matemtica 4
FRACTALES
Hoy vamos a hacer una excursin por la naturaleza: un frondoso bosque, una montaa encrespada, nubes blancas en el cielo.Difcilmente podemos representar los elementos de este paisaje utilizando la geometra clsica: la geometra de las rectas y las curvas la geometra de Euclides. Esta herramienta creada hace 2500 aos nos sirve para describir el mundo artificial creado por el hombre donde aparecen elementos regulares basados en lneas rectas y curvas simples.Como dijo Benoit Mandelbrot (1977), uno de los creadores de la geometra fractal, las nubes no son esferas, las montaas no son conos, las costas no son crculos, los relmpagos no se desplazan en lnea rectaSin embargo todos esos objetos tienen dentro de su irregularidad un orden asombroso:Su forma se va repitiendo a distintas escalas dentro del mismo objeto.Las ramas de un rbol o las hojas de un helecho reproducen a menor escala la estructura de la planta entera. Algo similar ocurre con las ramificaciones de nuestras venas y arterias o de nuestros pulmones, al aumentar la escala con la que nos acercamos al objeto, las irregularidades, en lugar de suavizarse, se mantienen al mismo nivel hacindolo semejante al modelo entero. Esta propiedad, tan difundida en la naturaleza, fue bautizada por Mandelbrot como autosemejanza.Qu es un fractal?En la geometra clsica los objetos tienen dimensiones enteras, as por ejemplo, una cuerda tiene dimensin uno, un polgono dimensin dos y una esfera es tridimensional.Sin embargo las curvas fractales pueden serpentear tanto dentro de un plano que casi llegan a rellenar las dos dimensiones del mismo. Por esta propiedad se asignan a estas curvasdimensiones fraccionarias, nmeros comprendidos entre uno y dos. Cuanto ms serpentee, ms prxima estar su dimensin a dos.Tras esta explicacin podemos resumir que los conjuntos fractales presentan todas o algunas de las siguientespropiedades: Tienen detalles a todas las escalas, entendiendo por esto que mirados a cualquier nivel de escala (zoom) manifiestan detalles ya observados a nivel global. Son autosemejantes, es decir, que estn formados por partes semejantes al conjunto total. Tienen una descripcin algortmica simple, entendiendo por ello que su construccin se basa en un algoritmo sencillo. Matemticamente un fractal puede obtenerse mediante la repeticin constante de un clculo simple: iteracin. Su rea o superficie es finita, es decir, tiene lmites. Por el contrario y por paradjico que esto resulte, su permetro o longitud es infinita, es decir, no tiene lmites.AplicacionesGracias a la geometra fractal de Mandelbrot son posibles las mediciones de la longitud de muchas porciones del mundo natural.As podemos medir lo accidentado de una costa mediante la dimensin fractal de una curva que se le asemeje. La curva fractal del copo de Koch se parece ms a una lnea de costa que a una lnea recta.Por procedimientos anlogos y utilizando superficies fractales en lugar de curvas se puede determinar la rugosidad de la superficie de los planetas. As la superficie terrestre tiene una dimensin fractal de 2,1. En cambio, la dimensin fractal de Marte es de 2,4, es decir, Marte es bastante ms accidentado que nuestro planeta.